Достатні умови екстремумА

Теорема. Нехай в околі стаціонарної точки функція має неперервні частинні

похідні до другого порядку включно. Обчислимо значення цих частинних похідних 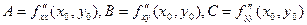у точці М а також число ,яке називають дискримінантом.

1) Якщо Δ>0, то у даній стаціонарній точці функція має екстремум.

Причому, при A < 0, або C <0 - максимум. A > 0,або C > 0 – мінімум.

2) Якщо Δ < 0, то у даній стаціонарній точці функція не має екстремума.

3) Якщо 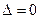, то питання відкрите.

Для знаходження екстремальниих точок функції двох змінних:

1. Обчислюють перші частинні похідні.

2.Із системи рівнянь ; знаходять стаціонарні точки системи М₁, М₂…

3. Обчислюють другі частинні похідні ; ; .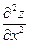

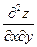4. Для точки М₁ обчислюємо числа А = 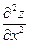(М₁); В= 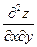(М₁); С= (М₁).

5. Обчислюємо число D =АС – В². Якщо 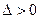, то в точці М₁ екстремум існує ( мінімум; 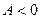максимум). Якщо , то в точці М₁ екстремум не існує.

6. Пункти 4-5 виконуємо для наступної стаціонарної точки М₂ , і т.д.

Приклад. Дослідити функцію 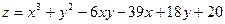на екстремум.

Знаходимо частинні похідні першого порядку:1) ; 2)

2) Знаходимо стаціонарні точки .

3) Знаходимо частинні похідні другого порядку: .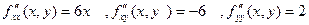

4) Перевіряємо першу стаціонарну точку на екстремум

Обчислюємо числа А,В,С і складаємо дискримінант . Отже, в точці М функція має екстремум, причому, і, оскільки то це – мінімум.

5) Перевіряємо першу стаціонарну точку на екстремум

Обчислюємо числа А,В,С 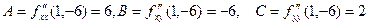і складаємо дискримінант . Отже, в точці N функція не має екстремума.

Дата добавления: 2015-08-02