Теорема Гаусса для вектора .
Магнитное поле и его характеристики. | За положительное направление нормали принимается направление поступательного движения правого винта, головка которого вращается в направлении тока, текущего в рамке. | Закон Био-Савара-Лапласа. Магнитное поле прямого тока и витка с током | Закон Ампера | Сила взаимодействия двух параллельных токов | Сила Лоренца | Период вращения частицы: - не зависит от скорости! | Циркуляция вектора для магнитного поля в вакууме | Контура с током в магнитном поле | Магнитные свойства вещества. Магнитные моменты электронов и атомов |
Потоком вектора магнитной индукции (магнитным потоком) через площадку  называется скалярная физическая величина, равная:
называется скалярная физическая величина, равная: 
 , где
, где  - проекция вектора
- проекция вектора 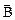 на направление нормали к площадке
на направление нормали к площадке  (рисунок 17), a - угол между векторами
(рисунок 17), a - угол между векторами 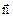 и
и 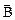 .
.  .
.
Поток вектора 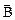 через произвольную поверхность
через произвольную поверхность 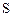 :
:
 .
.
Размерность потока:
Рисунок 17. Проекция вектора 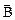 на нормаль на нормаль
| |
 (вебер)= 1 Тл×м2
(вебер)= 1 Тл×м2
Для однородного поля и плоской поверхности,
расположенных под углом:
где  - угол между вектором
- угол между вектором 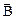 и нормалью к плоской поверхности.
и нормалью к плоской поверхности.
Дата добавления: 2015-08-02; просмотров: 69 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.005 сек.)

 называется скалярная физическая величина, равная:
называется скалярная физическая величина, равная: 
 , где
, где  - проекция вектора
- проекция вектора 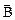 на направление нормали к площадке
на направление нормали к площадке  (рисунок 17), a - угол между векторами
(рисунок 17), a - угол между векторами 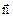 и
и 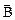 .
.  .
.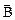 через произвольную поверхность
через произвольную поверхность 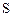 :
:
 .
. (вебер)= 1 Тл×м2
(вебер)= 1 Тл×м2
 - угол между вектором
- угол между вектором 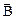 и нормалью к плоской поверхности.
и нормалью к плоской поверхности.