Циркуляция вектора для магнитного поля в вакууме
Магнитное поле и его характеристики. | За положительное направление нормали принимается направление поступательного движения правого винта, головка которого вращается в направлении тока, текущего в рамке. | Закон Био-Савара-Лапласа. Магнитное поле прямого тока и витка с током | Закон Ампера | Сила взаимодействия двух параллельных токов | Сила Лоренца | Теорема Гаусса для вектора . | Теорема Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен 0. | Контура с током в магнитном поле | Магнитные свойства вещества. Магнитные моменты электронов и атомов |
Циркуляция вектора 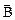 по заданному замкнутому контуру
по заданному замкнутому контуру 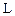 – это интеграл вида:
– это интеграл вида: 
 .
.
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора 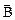 )
) 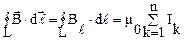 , где
, где
 – число проводников с током, охватываемых контуром
– число проводников с током, охватываемых контуром 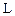 .
.
Циркуляция вектора 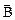 по произвольному замкнутому контуру
по произвольному замкнутому контуру 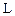 равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта (рисунок 14).
равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта (рисунок 14).
 . .
| |
Пример:
Поле, в котором циркуляция вектора 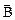 не равна 0, называется вихревым. Магнитное поле является вихревым.
не равна 0, называется вихревым. Магнитное поле является вихревым.
| Рисунок 14. К расчету суммы токов, охватываемых произвольным контуром
| |
Поле, циркуляция вектора которого равна 0, называется потенциальным полем (например, поле вектора напряженности электростатического поля  ).
).
Дата добавления: 2015-08-02; просмотров: 72 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.007 сек.)

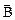 по заданному замкнутому контуру
по заданному замкнутому контуру 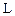 – это интеграл вида:
– это интеграл вида: 
 .
.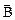 )
) 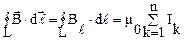 , где
, где – число проводников с током, охватываемых контуром
– число проводников с током, охватываемых контуром 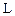 .
.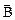 по произвольному замкнутому контуру
по произвольному замкнутому контуру 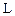 равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта (рисунок 14).
равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта (рисунок 14).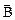 не равна 0, называется вихревым. Магнитное поле является вихревым.
не равна 0, называется вихревым. Магнитное поле является вихревым. ).
).