Читайте также:
|
Умножение и деление комплексных чисел проще выполнять, если они записаны в тригонометрической форме. Действительно, пусть комплексные числа 
и 
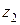заданы в тригонометрической форме:
, 
.
Перемножив их, получим:
.
Откуда, используя формулы для косинуса и синуса суммы, находим:
(3)
Итак, при умножении комплексных чисел их модули перемножаются, а аргументы – складываются.
Формула (3) очевидно остается верной для любого конечного числа множителей. В частности, при возведении числа 
в степень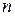 
(
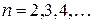) получим
. (4)
Формулу (4) называют формулой Муавра.
Теперь разделим на . Получим
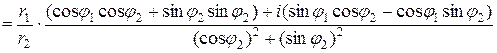
Но 
. Следовательно,
.
Откуда, используя формулы для косинуса и синуса разности, находим:
. (5)
Итак, при делении на получили комплексное число, модуль которого равен 
, а аргумент – 
.
Пример. Пусть 
, 
.
Тогда 
,
,
.
Дата добавления: 2015-08-02; просмотров: 83 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Действия над комплексными числами в алгебраической форме | | | Извлечение корня из комплексных чисел |