Читайте также:
|
Пусть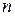 
– натуральное число. Корнем 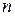–ой степени из комплексного числа 
(обозначают: 
) называют комплексное число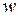 
, такое, что 
.
Пусть 
, 
. Тогда по определению и по формуле (5) получаем:
.
Отсюда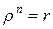 
, 
.
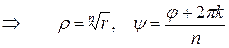Таким образом, все корни 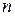–ой степени из комплексного числа 
могут быть найдены по формуле
, (6)
где 
.
Замечание. Формально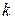 
в формуле (6) может принимать любое целое значение. Но угол 
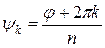и угол 
различаются на величину 
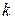. Следовательно, при и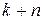 
мы получим по формуле (6) одно и то же комплексное число. Таким образом, различных значений корня будет только 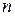, и чтобы их найти достаточно взять в формуле (6) .
Пример. Найти все значения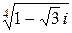 
.
Обозначим значения 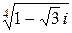через 
. Чтобы найти необходимо сначала записать комплексное число 
в тригонометрической форме. Имеем:
, 
,
, 
,
.
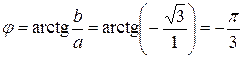Теперь по формуле (9) находим
,
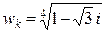
где 
. Или, более подробно:
,
,
,
.
Дата добавления: 2015-08-02; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Действия над комплексными числами в тригонометрической форме | | | Легкая атлетика |