Каскад реакторов идеального смешения

Каскад представляет собой несколько последовательно соединенных проточных реакторов (секций) идеального смешения

Исходные вещества

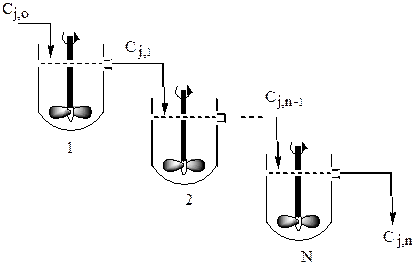Продукты

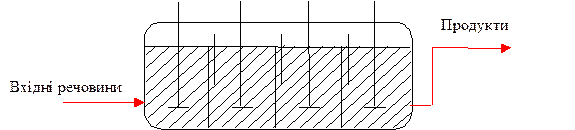
В единичном реакторе идеального смешения (РИС – Н) вследствие того, что концентрация реагентов мгновенно снижается до конечной величины, скорость реакции при большой степени превращения невелика, поэтому для достижения высокой степени превращения нужен реактор большого объема. Поэтому очень часто применяют ряд последовательно расположенных РИС – Н, т. е. К – РИС.

C

C_A

1 2 3 4 m

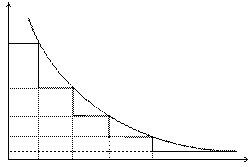
Концентрация исходного реагента в такой системе снижается до конечного значения не сразу, а постепенно от реактора к реактору.

Математическая модель каскада реакторов идеального смешения, работающего в изотермическом режиме, представляет собой систему уравнений материального баланса по какому – либо участнику реакции, включающую, по меньшей мере, N уравнений по числу секций каскада.

В расчете каскада для каждой ступени используется проектное уравнение проточного непрерывно действующего реактора идеального смешения. Пронумеруем последовательно ступени каскада от 1 до N. Обозначим через С_j,i концентрацию реагента j в смеси, покидающей i - ю ступень. Если предположить, что в трубопроводах, соединяющих аппараты каскада, химическое превращение минимальное, то можно считать концентрацию реагента j в смеси на выходе из i – го реактора равной концентрации этого вещества в смеси на выходе в (i + 1) реактор.

Используя уравнение

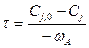
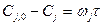
Последовательно для расчета отдельных ступеней каскада получаем:

,

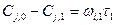
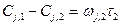
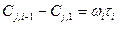
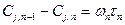где τ₁, τ₂ … τ_i , τ_п – среднее время пребывания реагентов в отдельных ступенях каскада.

Таким образом образовалась система N уравнений с N неизвестными С_j,1, C_j,2, …C_j,n, поскольку скорости реакции ω_j,1 = f(C_j), ω_j,i = f(C_j,i) … тоже являются функциями этих концентраций. Концентрации в отдельных реакторах вычислим путем последовательного решения проектных уравнений, начиная с первой ступени каскада.

В некоторых простых случаях, например для реакции первого порядка, можно установить непосредственную зависимость между концентрациями на входе в каскад и выходе из него.

,

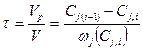где V_p – реакционный объем;

i – секции;

τ – среднее время пребывания реакционной смеси в i – ой секции;

С_j,i-1 – концентрация участника реакции на входе в i – ую секцию, равная концентрации на выходе из (i – 1) секции;

С_j,i – концентрация компонента на выходе из i – ой секции.

Расчет каскада обычно сводится к определению числа секций заданного объема, необходимого для достижения заданной степени превращения, или к определению состава реакционной смеси на выходе из i – ой секции каскада. Выходные параметры для первой секции являются входными для второй, и т. д.

Рассмотрим определение концентрации реагента А на выходе из каскада, имеющего N секций равного объема V₁ = V₂ … V_N при проведении реакции первого порядка.

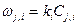
Получаем систему уравнений

.

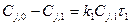
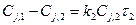
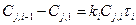
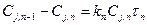Из первого уравнения находим концентрацию реагента j, в первой ступени каскада

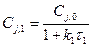(1)

Концентрация реагента j во втором реакторе

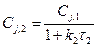, и т. д. (2)

Исключим из уравнений (1) и (2) С_j,i

.

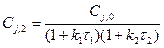Исключая таким же образом последующие промежуточные концентрации,

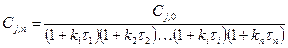
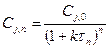, (3)

если константы скорости и время пребывания равны.

Если учесть, что 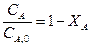, то уравнение (1) можно записать

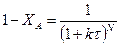
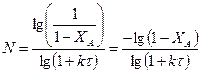
Уравнение (1) позволяет не только определить концентрацию на выходе из любого реактора каскада, но и найти число последовательно соединенных реакторов, если заданы изменения концентрации или степень превращения.

.

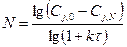Аналитическое решение уравнений для определения концентраций реакций более высокого порядка очень сложно. Поэтому в этом случае более предпочтителен менее точный, но более простой графический метод. Либо, так как уравнения материального баланса однотипны для всех секций, можно составить алгоритм решения этих уравнений для i – ой секции и последовательно применять его N раз.

В каждом реакторе концентрация исходного реагента в объеме постоянна и равна его концентрации на выходе из реактора. Изменение концентрации исходного вещества происходит так же, как и в РИС – Н, т. е. скачком при входе реакционной смеси в реактор. Однако концентрация С_А в каскаде выше, чем в единичном реакторе и при увеличении числа приближается к значению концентрации в РИВ.

Задачей расчета К – РИС является определение числа ступеней (числа реакторов), необходимых для достижения заданной степени превращения. Для определения числа ступеней каскада используют графический или алгебраический метод.

Дата добавления: 2015-08-10