Структура математической модели химического реактора

Классификация реакторов

При классификации реакторов принимают во внимание следующие основные признаки:

1. Характер операций, протекающих в реакторе

2. Режим движения реакционной среды

3. Тепловой режим

4. Фазовое состояние реагентов

По 1 признаку реакторы делят на периодические, непрерывные и полунепрерывные. Реакторы непрерывные, т. е. с непрерывной подачей реагентов, в свою очередь делят по характеру движения реакционной среды (т. е. по гидродинамической обстановке) на реакторы идеального вытеснения и реакторы идеального смешения.

Структура математической модели химического реактора

Методы расчета и проектирования химических реакторов основаны на моделировании реакторов и процессов в них.

Моделирование – это метод изучения различных объектов, при котором исследование проводят на модели, а результаты количественно распространяют на оригинал. Модель может представлять собой уменьшенную по определенным законам (или в некоторых случаях увеличенную) копию реального объекта. Но моделью может быть и определенная система представлений о реальном объекте, выражаемая как совокупность математических структур, уравнений, неравенств, таблиц, графиков. Такую модель называют математическим описанием объекта или его математической моделью.

Математическая модель химического реактора должна быть с одной стороны достаточно простой, с другой стороны – достаточно точно передавать количественные закономерности протекания процесса. Эти требования находятся в противоречии и разработка математической модели реактора весьма сложная задача.

При разработке математической модели целесообразно использовать иерархический подход к реактору как к сложной системе. (Иерархия – это расположение частей или элементов целого в порядке от высшего к низшему). Суть этого подхода состоит в том, что сложная система рассматривается как совокупность подсистем, связанных между собой.

Реактор и реакционный узел, будучи сложными объектами, имеют многоступенчатую структуру и их математические модели строятся последовательно на основе предварительного построения их составных частей и введения соотношений, связывающих переход с одного уровня на другой. Важную роль математического описания химического реактора играют балансовые уравнения, являющиеся выражением общих законов сохранения массы и энергии.

n_{j вх} – n_{j вых} -n_j X_р = n_{j нах},

где n_{j вх} – количество вещества j, внесенное в элементарный объем ΔV за время Δτ с потоком участников реакции.

Q_вх – Q_вых Q_хр Q_т.о. = Q_нач

Q_вх – теплосодержание веществ, входящих в объем ΔV за время Δτ;

Q_хр – теплота, выделившаяся или поглотившаяся в результате химической реакции;

Q_т.о – теплота, израсходованная на теплообмен объема ΔV за время Δτ;

Для составления материального баланса по веществу А будем считать, что объемный расход реакционной смеси на входе в реактор V₀, м³/ч, на выходе V. Концентрация вещества А в потоке, входящем в реактор C_A,0, кмоль/м³, концентрация вещества А в выходящем потоке и в любой точке реактора составляет C_A, кмоль/м³, химическая реакция протекает со скоростью W_A кмоль/м³ ч, определяемый и рассматриваемый промежуток времени dτ, при постоянной температуре, концентрации C_A.

Тогда за время dτ в объем реактора V войдет n_{A вх} = C_A,0 V₀ dτ, выйдет из реактора n_{A вых} = C_A V dτ. Израсходуется на химическую реакцию n_{A х.р.} = W V_р dτ.

Так как в реакторе находится C_AV_р моль вещества А, изменение этого количества за время dτ составит n_{A мак} = d (C_A V_р)

Таким образом уравнение материального баланса по веществу А для реактора идеального смешения имеет вид

C_A,0 V₀ dτ - C_A V dτ – W_A V_р d τ = d (C_A V_р)

Все члены этого уравнения измеряются в единицах количества вещества (кмоль). Разделим левую и правую часть на d τ

C_A,0 V₀ - C_A V - W V_р = (1) - мольные потоки вещества в единицу времени. Правая часть уравнения представляет собой скорость накопления вещества в реакторе. При постоянном объеме V_р скорость накопления можно представить

V_р dC_A / dτ

Рассмотрим отдельный случай. Периодический реактор идеального смешения по условию

V₀ = 0, V = 0.

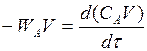или

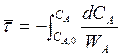C_A = C_A,0 (1 – X_A)

dC_A = - C_A,0 dX_A

Дата добавления: 2015-08-10