|
Читайте также: |
быть лишь тело, соприкасающееся с В;в схолии к т. 6, ч. II мы показали, что нет такого движения из одного места в другое, которое не требовало бы столь малого отрезка времени, меньше которого невозможно представить. Отсюда следует, что место, занимаемое телом В,но может быть занято в тот же момент другим телом, которое должно было бы пройти некоторое пространство, прежде чем занять это место. Следовательно, лишь тело, непосредственно касающееся В,может одновременно занять его место, что и требовалось доказать.
Схолия. Так как части материи действительно отличаются друг от друга (по § 61, ч. Т «Начал»), то одна может существовать без другой (по кор. к т. 7, ч. 1), и они но зависят друг от друга. Поэтому все вымыслы о симпатии и антипатии должны быть отвергнуты как ложные. Далее, причина всякого действия должна представлять нечто положительное (по акс. 8, ч. 1), а потому никогда нельзя сказать, что тело движется лишь для того, чтобы не возникло пустоты, но оно скорее нуждается для этого в толчке со стороны другого тела.
Королларий. При всяком движении движется одновременно целый круг тол.
Доказательство. В то время как тело 1 занимает место тела 2,последнее должно вступить на место другого тела,
235
например 3,и т.д. (по т. 7, ч. II). Далее, в то мгновение, когда тело 1 занимает место тела 2,место, оставленное телом 1,должно быть занято другим (по т. 8, ч. II), например телом 8 или другим, которое непосредственно касается тела 1. Но так как это может произойти лишь благодаря толчку со стороны другого тела (по предыдущей схолии), каковым здесь предполагается тело 1,то эти совместно движущиеся тела не могут находиться на одной прямой линии (по акс. 21), но описывают (по опр. 9) полный круг, что и требовалось доказать (см. фиг. 2).
Теорема 9
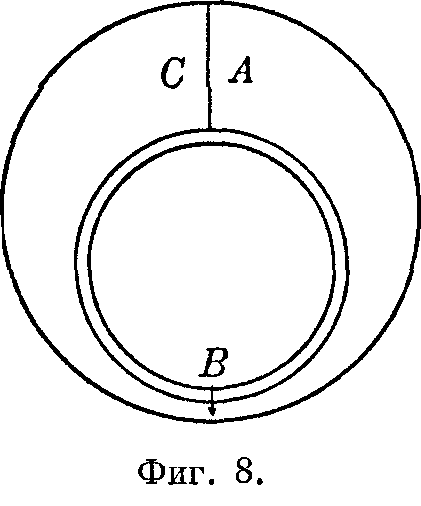Если круговой канал АВС наполнен водой и в месте А он вчетверо шире, чем в месте В, то в то самое время, когда вода (или другая жидкость), находящаяся в А, начинает двигаться к В, вода, находящаяся в B, будет двигаться вчетверо скорее.
Доказательство. Когда вся вода с места А движется к В,то одновременно столько же воды в С,соприкасающейся с А,должно занять ее место (по т. 8, ч. II), а из В столько же воды должна занять место С (по той же т.), следовательно, вода должна в месте В двигаться вчетверо скорее (по акс. 14), что и требовалось доказать. То, что здесь сказано о круговом канале, справедливо и для всех неравных пространств, через которые должны проходить одновременно движущиеся тела; доказательство этого будет тем же.
Лемма
Если два полукруга описываются вокруг того же центра, как А и В,топространство между обеими перифериями будет везде одинаковым. Если же они описываются около различных центров, как С и Д,то это простран-
235
ство между двумя окружностями будет везде неодинаковым
Доказательство. Очевидно из самого определения круга.
Теорема 10
Жидкость, движущаяся через канал АВС (см. фиг. 8), принимает бесконечно много различных скоростей.
Доказательство. Пространство между А и В везде неодинаково (но предыдущей лемме); поэтому скорость (по т. 9, ч. II), с которою жидкость движется через канал АВС,везде неодинакова. Так как далее между А и В можно мысленно себе представить бесконечно много все более мелких пространств (по т. 5, ч. II), то, очевидно, что неравенства пространства существуют повсюду в бесконечном числе, а потому и степени скорости будут бесконечно различны (по т. 9, ч. II), что и требовалось доказать.
Теорема 11
В материи, текущей через канал АВС (см. фиг. 8), существует разделение на бесконечное множество частиц.
Доказательство. Материя, текущая через канал АВС,имеет одновременно бесконечно много скоростей (по т. 10, ч. II), следовательно (по акс. 16), она имеет бесконечно много действительно различных частей, что и требовалось доказать (см. § 34 и 35, ч. II «Начал»),
Схолия. До сих пор мы рассуждали о природе движения. Теперь нам нужно исследовать его причину, которая двояка, а именно: первая, или всеобщая, причина, которая является причиной всех происходящих в мире движений, и частная причина, посредством которой отдельные части материи получают движения, которых они ранее не имели. Поскольку (по т. 14 и сх. к т. 17, ч. I) истинным
237
можно признавать лишь воспринятое ясно и отчетливо, то, очевидно, что всеобщей причиной можно считать только бога, потому что нельзя понять ясно и отчетливо никакой другой причины, кроме бога (как творца материи). То, что я здесь говорю о движении, имеет силу и для покоя,
Теорема 12
Бог есть главная причина (causa principalis) движения.
Доказательство. См. предыдущую схолию.
Теорема 13
То количество движения и покоя, которое бог однажды сообщил материи, и теперь еще сохраняется его содействием.
Доказательство. Так как бог есть причина движения и покоя (по т. 12, ч. II), то он сохраняет их той же силой, которой он их сотворил (по акс. 10, ч. I), а именно в том же количестве, в котором он их первоначально сотворил (по кор. к т. 20, ч. I), что требовалось доказать.
Схолия 1. Хотя в теологии говорится, что бог делает многое по своему усмотрению, чтобы показать людям свое могущество, однако то, что зависит лишь от его усмотрения, может быть понято только через божественное откровение, и потому в философии, где исследуется лишь то, чему учит разум, это не может быть допущено, так как философию не должно смешивать с теологией.
Схолия 2. Хотя движение представляет лишь состояние движущей материи, однако оно имеет известное и определенное количество; из последующего обнаружится, как это надо понимать (см. § 36, ч. II «Начал»).
Теорема 14
Всякая вещь, поскольку она проста и не разделена и поскольку она рассматривается сама по себе, остается всегда, поскольку это зависит от нее, в том же состоянии.
Эта теорема многим представляется как бы аксиомой, мы, однако, ее докажем.
Доказательство. Так как все может быть в определенном состоянии лишь с помощью бога (по т. 12, ч. I), а бог
238
в своих делах в высшей степени постоянен (по кор. к т. 20, ч. I), то, если не обращать внимания ни на какие внешние, т.е. особенные, причины, а рассматривать вещь самое по себе,следует утверждать, что она всегда будет оставаться в своем настоящем состоянии, что и требовалось доказать.
Королларий. Тело, раз пришедшее в движение, продолжает вечно двигаться, если не задерживается внешними причинами.
Доказательство. Это очевидно из предыдущей теоремы. Но, чтобы исправить ложные представления о движении, прочти § 37 и 38, ч. II «Начал философии» Декарта.
Теорема 15
Всякое движущееся тело само по себе стремится двигаться по прямой линии, а не по кривой.
Эту теорему следовало бы считать аксиомой, но я докажу ее из предыдущего.
Доказательство. Так как движение имеет причиной только бога (по т. 12, ч. II), то само по себе оно не имеет никакой силы существования (по акс. 10, ч. I), но в каждое мгновение как бы вновь создается богом (по доказанному в той же аксиоме). Поэтому, пока обращается внимание на одну только природу движения, никогда нельзя приписать ему такой, зависящей только от его природы, длительности, которая могла бы быть представлена больше другой. Если же сказать, что природа движущегося тела требует, чтобы оно описывало своим движением кривую линию, то надо приписать природе движения большую длительность, чем при допущении, что природа движущегося тела требует продолжения его движения по прямой линии (по акс. 17). Но так как (по доказанному) мы не можем приписать природе движения такой длительности, то нельзя также приписать ее природе движения по кривой, но только по прямой линии, что и требовалось доказать.
Схолия. Это доказательство для многих, может быть, покажется доказывающим только то, что природе движения одинаково свойственно описывать как кривую, так и прямую линию; и ото потому, что нельзя указать никакой прямой линии, менее которой но была бы возможна другая прямая или кривая линия, и никакой кривой,
239
в сравнении с которой но было бы другой менее кривой. Но и в этом отношении я считаю доказательство правильно построенным, так как оно выводит доказываемое из одной всеобщей сущности, т.е. из существенного различия линий, а не из какой-либо величины или случайного их различия. Но, чтобы в результате доказательства не сделать более темными вещи сами по себе ясные, я отсылаю читателей к самому определению движения, которое не утверждает о движении ничего, кроме того, что оно есть перенесение части материи из соседства одних в соседство других и пр. Если мы не представим этого перенесения простейшим, т.е. по прямой линии, то мы должны присоединить к движению нечто, не содержащееся в его определении или сущности и потому не принадлежащее к его природе.
Королларий. Из этой теоремы следует, что всякое тело, движущееся по кривой, постоянно отклоняется от линии, по которой оно двигалось бы само по себе, а именно в силу какой-либо внешней причины (по т. 14, ч. II).
Теорема 16
Всякое тело, движущееся по кругу, как, например, камень в праще, постоянно определяется к движению в направлении касательной.
Доказательство. Тело, движущееся по кругу, постоянно удерживается внешней силой от дальнейшего движения по прямой линии (по предыдущему королларию), а если эта сила прекращается, то тело само по себе начинает двигаться по прямой (по т. 15). Я говорю далее, что тело, движущееся по кругу, определяется внешней причиной к дальнейшему движению в направлении касательной. Оспаривая это, надо предположить, что, например, камень пращи в B определяется не в направлении касательной BD,но в другом направлении, которое представляется от этой точки внутри или вне круга, например по BF,когда праща представляется идущей из части L к В,или по ВС (о которой я предполагаю, что она образует с диаметром ВН угол, равный FBH),когда предполагается обратное движение пращи от С к В. Если же предположить, что в точке В камень пращи, движущейся по кругу от L к В,определяется к дальнейшему движению к F,то при дви-
240
женил пращи в обратном направлении от С к В камень необходимо должен (по акс. 18) продолжать движение в направлении, противоположном линии BF,и потому будет стремиться к K, а не к С,что противно допущению. Но так как * кроме касательной через точку В нельзя провести линии, образующей с линией Н с обеих сторон равные углы, подобно DBH и АВH,то лишь одна касательная в состоянии не противоречить одному и тому же допущению, как бы ни двигалась праща, от L к В или от С к В,и, следовательно, можно принять лишь касательную как линию, по которой камень стремится двигаться, что и требовалось доказать.
Другое доказательство. Возьмем вместо круга шестиугольник, вписанный в круг АВН,и пусть тело С на одной стороне АВ находится в покое, затем представим себе линейку DBE (один конец которой укреплен в центре D, а другой подвижен), которая движется вокруг центра и притом постоянно пересекает линию АВ. Очевидно, что при таком движении линейки DBE она встретит тело С в то мгновение, когда она пересечет линию АВ под прямым углом, и что своим толчком она заставит тело С двигаться по прямой линии FBAC по направлению к С,т.е. по стороне АВ,продолженной в бесконечность. Но мы взяли здесь шестиугольник совершенно произвольно, то же верно и для всякой иной фигуры, которую можно себе представить вписанной в круг. Именно, если тело С,находящееся в покое на одной стороне фигуры, получит толчок от линейки DBE в то мгновение, когда она пересекает эту сторону под прямым углом, то тело будет приведено
__________________
* Это очевидно из т. 18 и 19, кн. III «Элементов» Эвклида,
241
линейкой в движение по направлению этой стороны, продолженной в бесконечность. Поэтому если вместо шестиугольника представим себе прямолинейную фигуру с бесконечным числом сторон (т.е. круг, по определению Архимеда), то очевидно, что линейка DBE,где бы она ни встретила тело, всегда встретит его в то время, когда она пересечет одну сторону такой фигуры под прямым углом. Поэтому она никогда не встретит тела С,не приведя его одновременно в движение в направлении линии, продолженной в бесконечность. Но так как всякая сторона, продолженная по обоим направлениям, всегда должна пройти вне фигуры, то такая неопределенно продолженная сторона фигуры с бесконечным числом сторон, т.е. круга, будет всегда касательной. Если же представить себе вместо линейки пращу, движущуюся в круге, то она постоянно будет приводить камень в движение в направлении касательной, что и требовалось доказать.
Следует заметить, что оба доказательства можно отнести к любой криволинейной фигуре.
Теорема 17
Всякое тело, движущееся по кругу, стремится удалиться от центра круга, который оно описывает.
Доказательство. Пока тело движется по кругу, оно приводится в движение внешней причиной, с прекращением которой оно продолжает двигаться в направлении касательной (по предыдущей теореме), все точки которой, кроме той, где она касается круга, лежат вне круга (по т. 16, кн. II «Элементов» Эвклида) и потому дальше отстоят от него. Поэтому камень, находящийся в праще ЕА и движущийся по кругу, когда он находится в точке А,стремится двигаться по прямой, все точки которой отстоят от центра Е дальше, чем все точки окружности LAB,т.е. он стремится удалиться от центра описываемого им круга, что и требовалось доказать.
242
Теорема 18
Если тело, например А, движется к покоящемуся телу В, а В, несмотря на толчок А, не теряет своего покоя, то и В не потеряет ничего из своего движения, но удержит вполне то же количество движения, какое оно имело раньше.
Доказательство. Если кто оспаривает это, то допустим, что тело А теряет нечто из своего движения, не перенося потерянного движения на другое тело, например В. Тогда в природе окажется меньшее количество движения, чем прежде, что нелепо (по т. 13, ч. II). Таково же доказательство в отношении к покою тела В. Поэтому если ни одно из обоих тел ничего не переносит на другое, то В сохранит весь свой покой, а A все свое движение, что и требовалось доказать.
Теорема 19
Движение, рассматриваемое само по себе, отлично от своего определения следовать в том или другом направлении к определенному месту, и вовсе не необходимо, чтобы тело, движущееся или отталкиваемое в противоположную сторону, некоторое время покоилось.
Доказательство. Предположим, как в предыдущей теореме, что тело А движется по прямой линии к телу В и удерживается от дальнейшего движения телом В. При этом оно (по предыдущему) сохранит все свое движение и ни минуты не будет в покое. Но при продолжении своего движения оно не может удержать прежнего направления, так как, по допущению, оно задержано телом В. Поэтому оно, не уменьшая своего движения, но лишь изменяя свое направление, будет двигаться в противоположном направлении (согласно сказанному в гл. 2 «Диоптрики») 12. Поэтому (по акс. 2) направление не принадлежит сущности движения, но отлично от нее, и движущееся тело, отталкиваясь таким образом, ни минуты не остается в покое, что и требовалось доказать.
Королларий. Отсюда следует, что ни одно движение не противоречит другому.
243
Теорема 20
Если тело А встречает тело В и увлекает его за собой, то А потеряет столько движения, сколько В при этой встрече получит от А.
Доказательство (см. фиг. 1).Если кто-нибудь оспаривает это, то он тем самым допускает, что В получает больше или меньше движения, чем А теряет, тогда вся эта разница должна увеличить или уменьшить количество движения всей природы, что (по т. 13, ч. II) нелепо. Таким образом, если тело В не может получить ни меньше, ни больше, то оно может получить лишь столько, сколько А теряет, что и требовалось доказать.
Теорема 21
Если тело А вдвое больше тела В и движется с такой же скоростью, то тело А будет иметь вдвое больше движения, чем В, или вдвое больше силы, чтобы удержать равную с В скорость (см. фиг. 1).
Доказательство. Предположим, например, вместо А два В,т.е. (по допущению) А,разделенное на две части; тогда каждое из этих двух В будет иметь силу оставаться в том состоянии, в котором оно находится (по т. 14, ч. II), и эта сила в обоих одинакова (по предположению). Если же оба эти В связаны, то возникнет одно А,сила которого или количество равны обоим В,или вдвое больше одного В,что и требовалось доказать.
Впрочем, это следует также из простого определения движения. Именно, чем больше движущееся тело, тем более материи может отделиться от другого тела, следовательно, будет более отделения, т. е. (по опр. 8) более движения. См. наше четвертое замечание относительно определений движения.
Теорема 22
Если тело А равно телу В и движется вдвое скорее В, сила или движение в А будет вдвое больше, чем в В.
Доказательство. Допустим, что тело В при первоначальном его приведении в движение получило четыре
244
степени скорости. Если к этому ничего не присоединится, то оно будет продолжать свое движение (по т. 14, ч. II) и оставаться (perseverare) в своем состоянии. Теперь предположим, что оно благодаря новому толчку, равному первому, получает новую силу; тогда кроме первых четырех степеней оно получит новые четыре степени скорости, которые оно также удержит (по той же теореме), т.е. оно будет двигаться вдвое скорее или со скоростью, равной А,и одновременно будет иметь силу вдвое больше прежней, т.е. равную силе А. Следовательно, движение А вдвое больше движения В,что и требовалось доказать.
Надо заметить, что под силой в движущихся телах мы разумеем здесь количество движения, которое в телах равной величины должно возрастать со скоростью движения, поскольку посредством этой скорости равновеликие тела в равное время больше отделяются от непосредственно прилегающих тел, чем при более медленном движении, и потому (по опр. 8) обладают большим движением. Напротив, в покоящихся телах под силой сопротивления понимают количество покоя. Отсюда следует:
Королларий 1. Чем медленнее движутся тела, тем более они причастны покою,ибо они более сопротивляются встречным телам, движущимся быстрее и имеющим силу, меньшую, чем они сами, а также менее отделяются от непосредственно прилегающих тел.
Королларий 2. Если тело А движется вдвое скорее тела В, а В вдвое больше А, то в большем В столько же движения, как в меньшем А, следовательно, сила в обоих одинакова.
Доказательство. Если В вдвое больше А,а A движется вдвое скорее В,и далее С вдвое меньше В и движется вдвое медленнее А,то (по т. 21, ч. II) В будет иметь вдвое большее движение и (по т. 22, ч. II) А — вдвое большее движение, чем С, следовательно (по акс. 15), А и В будут иметь равное движение, так как движение обоих вдвое больше С,что и требуется доказать.
Королларий 3. Отсюда следует, что движение отлично от скорости. Ибо очевидно, что из двух тел, имеющих равную скорость, одно может иметь вдвое большее движение, чем другое (по т. 21, ч. II), и наоборот, тела с неравной скоростью могут иметь равное движение (по предыдущему королларию). Впрочем, это очевидно также из
245
простого определения движения, так как оно представляет лишь перенос тела из соседства и т.д.
Однако здесь надо заметить, что этот третий королларий не противоречит первому. Ибо скорость можно понимать двояким образом: или по тому, как одно тело более или менее отделяется от непосредственно прилегающего тела в равное время и поэтому более или менее участвует в покое или движении, или по тому, как оно в равное время описывает большую или меньшую линию и постольку отличается от движения.
Я мог бы здесь прибавить еще другие теоремы, чтобы лучше выяснить т. 14, ч. II и объяснить силы вещей во всяком состоянии, как это сделано здесь относительно движения. Но достаточно перечитать § 43, ч. II «Начал» и прибавить здесь лишь одну теорему, необходимую для понимания следующего.
Теорема 23
Если модусы какого-либо тела принуждены испытать перемену, то эта перемена всегда будет наименьшей.
Доказательство. Эта теорема довольно очевидно вытекает из теоремы 14, ч. II.
Теорема 24. Первое правило.
Если два тела, например А и В (см. фиг. 1), вполне равны друг другу и движутся друг к другу с равной скоростью, то при встрече их каждое отразится в противоположную сторону, не теряя своей скорости.
В этом предположении ясно, что для устранения противоположности этих двух тел или оба они должны отразиться в противоположном направлении, или одно должно увлечь за собой другое, так как они противоположны друг другу не в отношении движения, а лишь направления.
Доказательство. Если А и В сталкиваются, то они должны испытать некоторое изменение (по акс. 19). Но так как одно движение не противоположно другому (по кор.к т. 19, ч. II), то они нисколько не должны терять свое движение (по акс. 19). Поэтому изменение коснется
246
лишь направления. Но нельзя себе представить, что меняется лишь направление одного из этих тел, например В, в том случае, если А, от которого оно должно получить изменение, не будет предположено сильнее В (по акс. 20). Но последнее было бы противно допущению. Поэтому если перемена направления может произойти лишь у одного тела, то она произойдет у обоих, причем A и В отразятся в противоположном направлении (по изложенному в «Диоптрике», гл. 2), но сохранят все свое движение, что и требовалось доказать.
Теорема 25. Второе правило.
Если оба тела неравны по своей массе, именно В больше А (см. фиг. 1), остальные же предложенные условия остаются прежними, то отразится лишь А, и оба тела будут продолжать движение с равной скоростью.
Доказательство. Поскольку А предполагается меньше В,то оно имеет также меньшую силу, чем В (по т. 21, ч. II). Но так как при этом предположении, так же как и в предыдущем, противоположны лишь направления, и потому, как показано в предыдущей теореме, изменение может касаться только направления, то оно произойдет только в А,а не в В (по акс. 20); поэтому только А будет отражено более сильным В в противоположном направлении, не теряя, однако, нисколько своей скорости, что итребовалось доказать.
Теорема 26
Если тела различны, как по своей массе, так и по скорости, именно В вдвое больше А (см. фиг. 1), но движение А вдвое скорее В, а в остальном все остается по-прежнему, то оба тела отразятся в противоположном направлении и каждое удержит прежнюю скорость.
Доказательство. Так как А и В по предположению движутся друг против друга, то в одном столько же движения, как и в другом (по кор. к т. 22, ч. II). Поэтому движение одного не противоречит движению другого (по кор. к т. 19, ч. II) и силы обоих равны (но кор. 2 к т.22, ч. II). Таким образом, это предположение совер-
247
шенно подобно предположению т. 24, и потому, согласно предыдущему доказательству, А и В отразятся в противоположном направлении, и каждое при этом сохранит всю свою скорость, что и требовалось доказать.
Королларий. Из трех последних теорем очевидно, что направление тела требует для своей перемены столько же силы, как изменение движения. Отсюда следует, что тело, теряющее более половины своего определения следовать в данном направлении и более половины своего движения, испытывает большую перемену, чем тело, теряющее все свое определение.
Теорема 27. Третье правило.
Если два тела равны по массе, но В движется немного скорее А, то не только А отразится в противоположном направлении, но и В перенесет на А половину своего излишка скорости, и оба будут продолжать движение с равной скоростью в одном направлении.
Доказательство. А (по допущению) противоположно В не только по своему направлению, но и по медленности, поскольку последняя причастна покою (по кор. к т. 22, ч. II). Поэтому простым отражением в противоположном направлении изменяется только направление, но не устраняется вся противоположность обоих тел. Следовательно (по акс. 19), перемена должна наступить как в направлении, так и в движении, и так как В по допущению движется скорее А,то В (по т. 22, ч. II) сильнее А,и потому (по акс. 20) перемена в А произойдет через В,и А будет посредством В отражено в противоположном направлении. Это первое. Далее, А,пока оно движется медленнее В,противоположно последнему (по кор. 1 к т. 22, ч II), следовательно, должна наступить перемена (по акс. 19), по которой А не будет двигаться медленнее В. Но А не принуждается при этом допущении никакой достаточно сильной причиной к тому, чтобы двигаться скорее В.
Таким образом, если А не может двигаться медленнее В,так как оно сталкивается с В,ни скорее В,то А должно двигаться с такой же скоростью, как В. Но, если бы В переносило на А менее половины своего излишка скорости, то А продолжало бы двигаться медленнее В;а если бы В переносило более половины своего излишка скорости на
248
А,то А двигалось бы скорее В. Но, как уже показано, то и другое нелепо. Поэтому перемена будет происходить лишь, пока В не перенесет на А половину своей большей скорости, которую В должно потерять (по т. 20, ч. II), и, следовательно, оба будут продолжать движение с равной скоростью в том же направлении без всякого противоречия, что и требовалось доказать.
Королларий. Отсюда следует, что, чем скорее движется тело, тем более оно определено продолжать движение в направлении линии своего следования, и наоборот, чем оно медленное движется, тем менее оно склонно к этому.
Схолия. Для того чтобы читатели не смешали здесь силу направления с силой движения, кажется, неплохо прибавить несколько замечаний, отчего станет яснее различие обоих. Итак, если предположить, что тела А и С равной величины и движутся с равной скоростью прямо друг против друга, то оба (по т. 24, ч. II) отразятся в противоположном направлении, удержав все свое движение. Если же тело С находится в B и движется косвенно к А,то, очевидно, оно ужо менее склонно двигаться в направлении BD или С А (см. фиг. 13). Поэтому оно, правда, имеет одинаковое движение с А,но сила направления тела С, если оно движется прямо по направлению к В,которая тогда одинакова с силой направления А,больше силы направления С,если оно движется от В к А,а именно настолько больше, насколько линия В А больше С А. Ибо, чем больше линия С А,тем более времени (именно, если В и А движутся, как здесь допущено, с одинаковой скоростью) требует В,чтобы двигаться в направлении BD или С А,по которому оно движется прямо противоположно направлению тела А. Итак, если С идет из В навстречу А косвенно, то оно направляется так, как будто оно продолжало двигаться в направлении АВ’ к В’ (я предполагаю, что, когда С находится в точке, где линия АВ’ пересекает продолженную линию ВС,то эта точка отстоит от С так же далеко, как С от В).Напротив, А удерживает все свое движение и направление и продолжает свое движение к С и захватит тело В с собой, так как В,имея при своем движении направление по диагонали АВ’, требует больше времени, чем А,для прохождения части линии АС и лишь постольку противоположно направлению более сильного тела А. Но сила направления С,движущегося из В к А,поскольку оно совпадает с линией
Дата добавления: 2015-08-10; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ГЕОМЕТРИЧЕСКИМ 4 страница | | | ГЕОМЕТРИЧЕСКИМ 6 страница |