Определение угла профиля a.

Шарик поджат пружиной с усилием F_пр к рабочим поверхностям впадины с углом профиля a сопряженной полумуфты. Крутящий момент передается от полумуфты 1 через шарик к полумуфте 2 окружным усилием F_t.

При перегрузке шарик, преодолевая усилие пружины, перемещается в направлении V_шар, скользит по наклонной поверхности впадины полумуфты 2. В конечном итоге, шарик полностью выходит из впадины и перескакивает в соседнюю впадину.

Рассмотрим силы, действующие на шарик в момент выхода его из впадины полумуфта 2.

Со стороны наклонной поверхности на шарик действует нормальная сила F_N и сила трения F_{f 2}. Геометрической суммой этих сил будет усилие F_R. Угол j между нормальной и результирующей силами называется углом трения, определяется он через коэффициент трения f

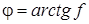. (1)

Разложим F_R на две составляющих: горизонтальную - F_A и вертикаль- ную - F_{t 2}. F_{t 2} – окружное усилие, действующее на шарик со стороны полумуфты 2. F_A – осевое усилие, действующее на шарик со стороны полумуфты 2. Соотношение между этими силами определится из «зеленого» треугольника:

. (2)

Со стороны полумуфты 1 на шарик действует окружное усилие F_{t 1} и сила трения F_{f 1} в точке А.

Спроецируем силы, действующие на шарик, на горизонтальную ось

, (3)

отсюда

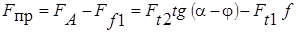, (4)

поскольку

, (5)

то

(6)

Проанализируем уравнение (6). Примем

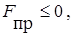(7)

тогда,

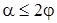. (8)

Соотношение (8) называется условием самоторможения. При соблюдении этого условия муфта не расцепится при любом моменте и будет работать как простая жесткая муфта.

Для того, чтобы муфта расцеплялась при достижении предельно момента, то есть выполняла функции предохранительной муфты, следует принять

. (9)

Это есть условие работоспособности муфты.

При затрудненных условиях смазки коэффициент трения между шариком и полумуфтами можно принять f = 0,15, тогда

,

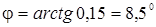или

. (10)

Для надежности срабатывания муфты принимают

. (11)

2. Контактная прочность шарик – боковая плоскость впадины.

Для точечного контакта сфера – плоскость

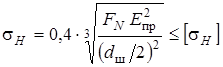. (12)

Примем [s _H ] = 2500 Мпа и решим относительно

(13)

E = 2×10⁵ Мпа.

Крутящий момент

(14)

где F_t [Н] – окружное усилие, передаваемое одним шариком, на диаметре

D ₀ [мм] расположения шариков;

Z – число шариков.

На основании чертежа выразим F_t через нормальную силу F_N

. (15)

Выразим D ₀ через шаг t расположения шариков на окружности этого диаметра

(16)

примем шаг расположения шариков из условия равенства ширины впадины и выступа на диаметре D ₀

(17)

Тогда

. (18)

Подставим в (14) выражения (15) и (18). Умножим и разделим правую часть на (d _ш)² . В полученное уравнение, подставив (13), решим относительно

. (19)

Таким образом, из условия контактной прочности, задаваясь диаметром шарика, определим число шариков

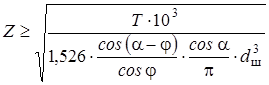. (20)

Диаметр расположения шариков определяется уравнением (18).

Для угла профиля a = 30⁰ и угла трения j = 8,5⁰

,

,

T – в Нм, d _ш – в мм.

Окружное усилие на одном шарике

.

Нормальное усилие

.

Усилие, действующее на пружину

.

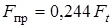Осадка пружины X

При выходе из впадины шарик должен переместиться в направлении сжатия пружины на величину X. Минимальное значение X, когда шарик контактирует с боковой поверхностью впадины в точке B

. (26)

С некоторым запасом можно принять

. (27)

При a = 30⁰

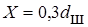. (28)

---

Дата добавления: 2015-08-10