Пример решения РГР № 1

1. Вычерчиваем эскиз стержня с приложенными силами, выдерживая масштаб размеров по его длине (рис. 2).

2. Число участков стержня – 3.

3. Вычисляем на каждом участке величину продольной силы.

Участок I: 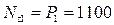кН (растяжение)

Участок II: кН.

Участок III: кН (сжатие).

Эпюра продольных сил показана на рис. 2, а.

Реакция в заделке составила R _А = 300 кН. Произведем проверку. Сумма всех внешних сил, приложенных к стержню, равна 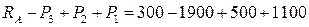"0": = 0.

4. Рассчитываем напряжения для каждого участка стержня по формуле s _i = N_i / F_i, (рис. 2, б). МПа,

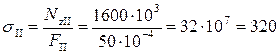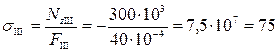МПа.

МПа.

Рис. 2. Пример построения эпюр N_z, s, D l

5. Рассчитываем абсолютные деформации каждого участка.

м.

м.

м.

6. Для построения эпюры продольной деформации стержня следует начало координат поместить в заделке (рис. 2, в). На границе между III и II участком укорочение стержня составит 0,3 мм, на границе II и I участка абсолютная деформация составит мм. Концевое сечение стержня сместится на 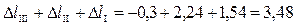мм. Следовательно, под действием внешних сил стержень удлинился на 3,48 мм.

Схема статически неопределимого стержня показана на рис. 3. Наличие двух заделок на концах стержня создает две реакции R_A и R_В, эти силы являются внешними и для их определения недостаточно использовать только уравнение статики . .

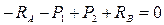Необходимо ввести еще одно дополнительное уравнение, которое составим на основании деформаций стержня.

Рис. 3. Расчетная схема статически неопределимого стержня

Определим деформацию каждого участка. I участок 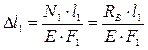. II участок . III участок . IV участок . V участок .

Стержень расположен между двумя жесткими заделками, поэтому его длина не может измениться. Второе уравнение, которое позволит раскрыть статическую неопределимость – уравнение совместности перемещений.

.

Подставляем в это уравнение деформации участков с численными значениями, из чего определим неизвестную реакцию R _В. Величину Е в этом уравнении можно не учитывать.

.

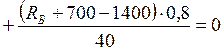Приводим уравнение к общему знаменателю, решаем его и находим, что R_В = - 271,84 кН. Знак "-" указывает на то, что принятое направление реакции следует изменить в обратную сторону.

Реакцию в заделке А определим из уравнения статики .

, R_А = 971,84 кН. Знак «+» указывает на то, что принятое направление реакции R_А выбрано верно.

Определение величины продольной силы, напряжений и деформаций для статически неопределимого стержня проводится по той же методике, что и для статически определимого стержня. Эпюры сил, напряжений и деформаций показаны на рис. 4.

Рис. 4. Эпюры продольных сил, напряжений и деформаций для статически неопределимого стержня

Условие выполняется, следовательно, продольные силы и деформации стержня определены верно.

Дата добавления: 2015-08-10