4 страница. 2.1.5 В прямоугольном параллелепипеде ____

Читайте также:

____________________________________________________________________

2.1.4 ___________________________________________________________________

____________________________________________________________________

2.1.5 В прямоугольном параллелепипеде ____________________________________

____________________________________________________________________

2.1.6 В правильной треугольной призме _____________________________________

____________________________________________________________________

2.2. Допуск к работе

2.2.1 Заполните пропуски

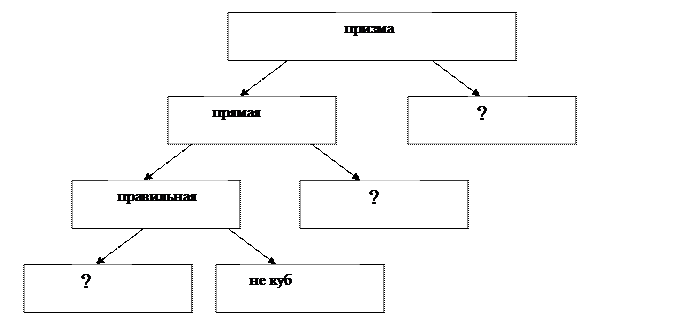
2.2.2 Заполните таблицу

Название	Основание	Взаимное расположение боковых рёбер и основания
Правильная треугольная призма	Правильный треугольник	Боковое ребро перпендикулярно основанию
Правильная четырёхугольная призма
Прямой параллелепипед
Прямоугольный параллелепипед
Наклонный параллелепипед
Прямая треугольная призма
Куб
Прямая четырёхугольная призма

2.2.3 Дана правильная четырёхугольная призма АВСДА₁В₁С₁Д_1.Запишите теорему Пифагора для треугольника В₁ДВ.

_______________________________________________________________________

2.2.4 Заполните таблицу

Фигура	Радиус вписанной окружности	Радиус описанной окружности
Правильный треугольник (равносторонний треугольник)
Правильный четырёхугольник (квадрат)
Правильный шестиугольник

К работе допускается ______________

3. Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 23

Нахождение основных элементов пирамид.

1. Цель работы

1. 1 Научиться изображать пирамиду и находить длину основных элементов, используя определение и свойства пирамид

2. Ход работы

2.1. Вариант

2.1.1

____________________________________________________________________

2.1.2 В треугольной пирамиде площадь основания равна см², площадь параллельного сечения см², расстояние от сечения до вершины пирамиды равно см. Найдите высоту пирамиды.

2.1.3 Основание пирамиды – прямоугольник со сторонами и см; каждое боковое ребро пирамиды равно см. Найдите высоту пирамиды.

2.1.4 В правильной треугольной пирамиде боковое ребро равно см и образует с плоскостью основания угол ⁰. Найдите сторону основания пирамиды.

2.1.5 В правильной треугольной пирамиде по стороне основания м и боковому ребру м определить площадь сечения, проведенного через боковое ребро и высоту пирамиды.

2.1.6 Длины сторон основания правильной четырехугольной усеченной пирамиды равны и см, длина бокового ребра равна см. Найдите площадь диагонального сечения.

2.2. Допуск к работе

2.2.1 SABC - правильная треугольная пирамида, SO - высота пирамиды. Запишите теорему Пифагора для треугольника SAO.

__________________________________

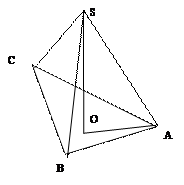
2.2.2 Найдите неизвестный член пропорции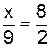

2.2.3 Дан прямоугольный треугольник АВС. Найдите синус угла САВ

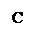
2.2.4 Продолжите утверждение:

А) Если боковые рёбра пирамиды равны, то основание высоты, проведённой из вершины на основание совпадает_______________________________________

____________________________________________________________________

Б) Если все боковые грани пирамиды образую с плоскостью основания равные двугранные углы, то основание высоты, проведённой из вершины на основание совпадает ____________________________________________________________

____________________________________________________________________

В) Апофемой правильной пирамиды называется __________________________

________________________________________________________________________________________________________________________________________

2.2.5 АВСДА₁В₁С₁Д₁– усечённая пирамида. Какой фигурой является четырёхугольник АА₁С₁С? _____________________________________________

Запишите формулу для вычисления площади этого четырёхугольника

К работе допускается ______________

3. Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 24

Нахождение основных элементов цилиндра, конуса, шара.

1. Цель работы

1. 1 Научиться находить основные элементы цилиндра, конуса, шара.

2. Ход работы

2.1. Вариант

2.1.1

____________________________________________________________________

2.1.2

____________________________________________________________________

2.1.3 ____________________________________________________________________

____________________________________________________________________

2.1.4

____________________________________________________________________

2.1.5 ____________________________________________________________________

____________________________________________________________________

2.1.6 ____________________________________________________________________

____________________________________________________________________

2.1.7 ____________________________________________________________________

____________________________________________________________________

2.1.8 ____________________________________________________________________

____________________________________________________________________

2.2. Допуск к работе

2.2.1 Назовите осевое сечение цилиндра и начертите диагональ осевого сечения.

______________________________

2.2.2 Выпишите: радиус цилиндра ___________________________

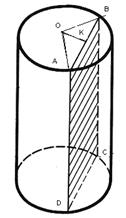
сечение цилиндра плоскостью, параллельной его оси ___________

расстояние от оси цилиндра до секущей плоскости_____________

2.2.3 Запишите образующую конуса __________________________

Угол наклона образующей к плоскости основания

_____________________________________________

Теорему Пифагора для треугольника SAO

____________________________________________

2.2.4 Назовите высоту ______________ и образующую _______________

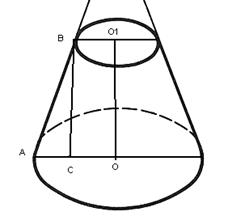усечённого конуса

2.2.5 Опишите около цилиндра треугольную призму.

2.2.6 Впишите в четырёхугольную пирамиду конус.

К работе допускается ______________

3. Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 25

Нахождение объёмов и площадей поверхности призмы и пирамиды.

1. Цель работы

1. 1 Научиться вычислять объёмы и площади поверхностей приз и пирамид.

2. Ход работы

2.1. Вариант

2.1.1 В основании прямой призмы прямоугольный треугольник с катетами см

и см. Найти объём и площадь полной поверхности призмы, если её высота

см.

2.1.2 Основание прямой призмы – прямоугольник со сторонами см и см. Диагональ призмы составляет с плоскостью основания угол . Найти объём призмы и площадь полной поверхности.

2.1.3 В правильной треугольной пирамиде длина стороны основания см, боковое ребро см. Найти объём и площадь полной поверхности пирамиды.

2.1.4 В правильной четырёхугольной усечённой пирамиде длины сторон оснований

см и см. Длина бокового ребра см. Найти объём пирамиды.

2.1.5 Найти объём правильной четырёхугольной призмы, если площадь полной поверхности , а площадь боковой поверхности .

2.2. Допуск к работе

2.2.1 Выпишите формулы для вычисления площадей многоугольников

Квадрат
Правильный треугольник
Прямоугольный треугольник
Произвольный треугольник
Трапеция

2.2.2 Выпишите формулы для вычисления площадей поверхностей и объёмов многогранников

Многогранник	Объём	Площадь боковой поверхности	Площадь полной поверхности
Прямая призма
Правильная пирамида
Усечённая правильная пирамида

2.2.3 Дана прямая призма, в основании которой – прямоугольник. Запишите угол, который образует диагональ В₁Д с плоскостью основания

_____________________

Вычислите синус этого угла ____________

К работе допускается ______________

3. Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 26

Вычисление объёмов и площадей поверхностей

цилиндра, конуса, шара.

1. Цель работы

1. 1 Научиться применять формулы для вычисления объёмов и площадей поверхности цилиндра, конуса, шара.

2. Ход работы

2.1. Вариант

2.1.1 Высота цилиндра см, площадь осевого сечения см². Найти площадь боковой поверхности, площадь полной поверхности и объем цилиндра.

2.1.2 Площадь основания конуса равна p см², а высота см. Найти площадь боковой поверхности, площадь полной поверхности и объем конуса.

2.1.3 Радиусы оснований усеченного конуса см и см, образующая см. Найти площадь боковой поверхности, площадь полной поверхности и объем усеченного конуса.

2.1.4 Шар пересечен плоскостью на расстоянии см от центра. Радиус сечения равен см. Найти объем шара и площадь поверхности сферы.

2.1.5 В цилиндр, высота которого см, вписана правильная четырехугольная призма со стороной основания см. Вычислить площадь боковой поверхности, площадь полной поверхности цилиндра и его объем.

2.1.6 Конус, высота которого см, вписан в правильную треугольную пирамиду со стороной см. Найти площадь боковой поверхности, площадь полной поверхности и объем конуса.

2.2. Допуск к работе

2.2.1 Выпишите формулы для вычисления площадей поверхностей и объёмов круглых тел

Многогранник	Объём	Площадь боковой поверхности	Площадь полной поверхности
Цилиндр
Конус
Усечённый конус
Шар

2.2.2 Найдите образующую конуса m через высоту h и радиус основания r

____________________________________________

2.2.3 Назовите радиус сферы ______________ расстояние от центра сферы до секущей плоскости _______________, радиус сечения

2.2.4 Зная, высоту и радиусы оснований усечённого конуса вычислите образующую конуса.

К работе допускается ______________

3. Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 27

РЕШЕНИЕ КОМБИНАТОРНЫХ ЗАДАЧ

1 Цель работы

1.1. Научиться определять тип выборки.

1.2. Научиться применять правила сложения и умножения.

1.3. Научиться находить число перестановок, число сочетаний, число размещений.

2. Ход работы

2.1 Вариант

2.1.1 Вычислить: .

2.1.2 Вычислить число ____________________________________________________________________________________________________________________________________

2.1.3 Вычислить число ____________________________________________________________________________________________________________________________________

2.1.4 Вычислить:

Решить задачу:

2.1.5 _________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________

2.1.6_________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________

_____________________________________________________________________________

2.1.7 _________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________

2.1.8 _________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________

2.1.9 _________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________

2.1.10 Найдите разложение степени бинома ()

2.2 Допуск к работе.

Ответить на вопросы:

1. Чем отличаются размещения от сочетаний?_______________________________

______________________________________________________________________

2. Сформулируйте правило сложения ______________________________________

3. Какие задачи называются комбинаторными?______________________________

______________________________________________________________________

В таблицу внести букву правильного, по вашему мнению, ответа.

1. Какая из данных формул – формула размещений:

а) 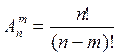; б) ; в)

2. Выбрать правильное предложение:

а) Произведение всех натуральных чисел от 1 до n включительно есть n!

б) Произведение натуральных чисел до n включительно называют n!.

в) Произведением чисел от 1 до n включительно есть n!.

3. Вычислить: 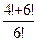а) 31; б) 3; в)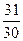

4. Упростить: а)

5. Как правильно прочитать :

а) «а» из «эм» по «эн»; б) «а» по «эн» из «эм»; в) «а» из «эн» по «эм».

6.Сократить дробь а) (n-6)(n-5); б) (n-5)(n-4); в)

7. Вычислите а) 30 б) 5 в) 0,2

К работе допускается ______________

3. Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 28

ВЕРОЯТНОСТЬ

1 Цель работы

1.1Закрепить классическое определение вероятности.

1.2 Научиться применять определение вероятности и её свойства при решении задач.

2 Ход работы

2.1. Вариант

2.1.1 Запишите определение _____________________________ события

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2.1.2

______________________________________________________________________________________________________________________________________________________________________________________________________

2.1.3

______________________________________________________________________________________________________________________________________________________________________________________________________

2.1.4

______________________________________________________________________________________________________________________________________________________________________________________________________

2.1.5

______________________________________________________________________________________________________________________________________________________________________________________________________

2.1.6

Дискретная случайная величина задана законом распределения

Х
Р

Построить многоугольник распределения.

Найти математическое ожидание случайной величины Х, дисперсию и среднее квадратическое отклонение

2.1.7

______________________________________________________________________________________________________________________________________________________________________________________________________

2.2 Допуск к работе.

2.2.1.Дайте определение вероятности ____________________________________________

__________________________________________________________________________________________________________________________________________________________

2.2.1 Перечислите свойства вероятности__________________________________________

______________________________________________________________________________________________________________________________________________________

2.2.2 Выберите в предложенных ответах один правильный и соответствующую букву впишите в таблицу.

1.Вычислите а) 5; б) 1; в) 0.

2. Какова вероятность того, что при подбрасывании игральной кости выпадет чётное число очков? а) 0,5 б) 0,3 в) 0,2

3. Какова вероятность, что извлечённый из урны шар будет одноцветным, если в ней 4 красных, 5 чёрных, 6 в полоску и 7 в клетку шаров?

а) б) в) г) 0

4. В каких пределах заключено значение вероятности любого события?

а) 0 < Р(А) ≤1 б) 0 ≤ Р(А) <1 в) 0≤ Р(А) ≤ 1 г) 0 < Р(А) < 1

Дата добавления: 2015-08-10; просмотров: 99 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
3 страница	\|	5 страница

mybiblioteka.su - 2015-2024 год. (0.049 сек.)