
|
Читайте также: |
 2.2. Допуск к работе
2.2. Допуск к работе
2.2.1. В чём заключается физический смысл производной
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.2.2. Каков геометрический смысл производной?
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.2.3. Запишите уравнение касательной к графику функции
________________________________________________________________________________________________________________________________________________
2.2.4. Запишите алгоритм нахождения наибольшего и наименьшего значения функции на отрезке
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________
2.2.5. Запишите формулу для вычисления приближённого значения функции
________________________________________________________________________________________________________________________________________________
________________________________________________________________________
К работе допускается ______________
3. Результаты работы
 ПРАКТИЧЕСКАЯ РАБОТА 16
ПРАКТИЧЕСКАЯ РАБОТА 16
Вычисление неопределённых интегралов
1. Цель работы
1. 1 Научиться вычислять неопределённые интегралы
2. Ход работы
2.1. Вариант
Вычислить интегралы:
| 2.1.1. | |
| 2.1.2 | |
| 2.1.3 | |
| 2.1.4 | |
| 2.1.5 | |
| 2.1.6. | |
| 2.1.7 | |
| 2.1.8 |
2.1.9 Скорость прямолинейного движения материальной точки задаётся формулой
v(t) =
Найдите закон движения S(t), если в момент времени t = с координата точки
равнялась.
2.1.10 Для функции у(х) = найдите первообразную, график которой проходит через точку М(;)
 2.2. Допуск к работе
2.2. Допуск к работе
2.2.1 Заполните таблицу интегралов
1) 
2) 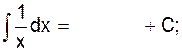
3) 
4) 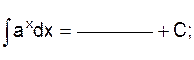
5) 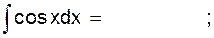
6) 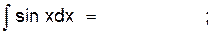
7) 
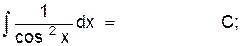
8) 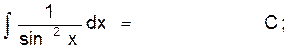
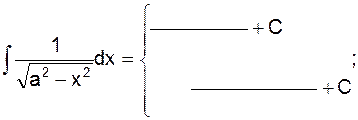
9) 
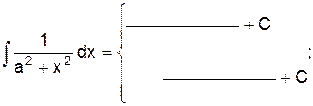
10) 
К работе допускается ______________
3. Результаты работы
 |
 ПРАКТИЧЕСКАЯ РАБОТА 17
ПРАКТИЧЕСКАЯ РАБОТА 17
Вычисление определённых интегралов.
1. Цель работы
1. 1 Научиться вычислять определённые интегралы
2. Ход работы
2.1. Вариант
Вычислить интегралы:
| 2.1.1. | |
| 2.1.2 | |
| 2.1.3 | |
| 2.1.4 | |
| 2.1.5 | |
| 2.1.6. | |
| 2.1.7 | |
| 2.1.8 | |
| 2.1.9. | |
| 2.1.10. |
2.2. Допуск к работе
2.2.1 Выпишите формулу Ньютона - Лейбница
__________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.2.2 Вычислите
| функция | х =0 | х = 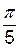
| х = 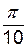
| х = 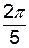
|
| y = cos5x | cos(5· 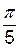 )=cos )=cos 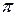 = -1 = -1
| |||
| y = sin5x |
 |
| функция | х =1 | х = 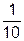
|
х = 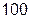
| х = 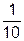
|
| y = lg x |
| функция | х =1 | х = e | х = e - 3 | х = e14 |
| y = ln x |
К работе допускается ______________
3. Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 18
Вычисление площадей плоских фигур с помощью
определённого интеграла.
1. Цель работы
1. 1 Научиться вычислять площади плоских фигур с помощью определённого интеграла
2. Ход работы
2.1. Вариант
Вычислить площадь фигуры, ограниченной линиями:
| 2.1.1. |
| 2.1.2 |
| 2.1.3 |
| 2.1.4 |
| 2.1.5 |
2.2. Допуск к работе
2.2.1 Выпишите формулу для вычисления площади, заштрихованной фигуры
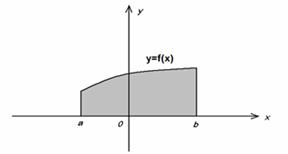
__________________________
 |
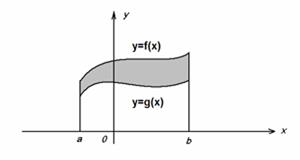
____________________________
2.2.2  Начертите график функции
Начертите график функции
у = 2 х
| 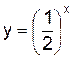

|
y= log 2 x
| 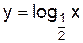

|
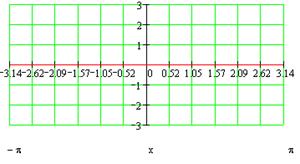
y = sinx
| y = 2sinx

|
К работе допускается ______________
3. Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 19
Решение задач на параллельность в пространстве.
1. Цель работы
1. 1 Научиться решать задачи, применяя свойства параллельности прямых и плоскостей в пространстве
2. Ход работы
2.1. Вариант
2.1.1 Дан прямоугольный параллелепипед АВСДА1В1С1Д1.
Найдите две прямые, параллельные:
а)прямой __________________, б) плоскости ________________.
Найдите плоскости параллельные:
а) прямой _________________ б) плоскости _________________
2.1.2 Через концы отрезка АВ и его середину М проведены параллельные прямые,
пересекающие некоторую плоскость в точках А1, В1, М1. Найдите ____________
_______________________________________________________________________
_______________________________________________________________________
если отрезок АВ не пересекает плоскость.
2.1.3. Точка А - конец отрезка АВ лежит в плоскости. Через конец В и точку М,
принадлежащей отрезку АВ, проведены параллельные прямые, пересекающие
данную плоскость в точках В1, М1 соответственно. Найдите _________________
_______________________________________________________________________
_______________________________________________________________________
2.1.4 Дан треугольник АВС. Плоскость, параллельная прямой АС пересекает сторону АВ
этого треугольника в точке А1, а сторону ВС в точке С1. Найдите _______________
_______________________________________________________________________
_______________________________________________________________________
2.1.5 Две плоскости 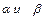 параллельны между собой. Из точки М, лежащей по одну
параллельны между собой. Из точки М, лежащей по одну
сторону от них, проведены две прямые, пересекающие плоскость 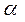 в точках
в точках
А1и А2, а плоскость 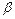 в В1 и В2 соответственно. Найдите ___________________
в В1 и В2 соответственно. Найдите ___________________
_______________________________________________________________________
_______________________________________________________________________
2.2. Допуск к работе
2.2.1  Дайте определение параллельных прямых в пространстве:
Дайте определение параллельных прямых в пространстве:
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
 |
2.2.2 Дайте определение параллельных плоскостей
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
2.2.3 Сформулируйте признак параллельности плоскостей
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
2.2.4 Заполните пропуски
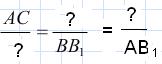
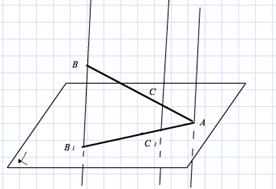
2.2.5 Запишите формулу для вычисления длины отрезка ММ1, если М – середина АВ, а отрезки ММ1, АА1, ВВ1 - параллельны
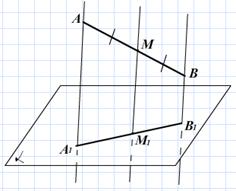
______________________________________
К работе допускается ______________
3. Результаты работы
 ПРАКТИЧЕСКАЯ РАБОТА 20
ПРАКТИЧЕСКАЯ РАБОТА 20
Решение задач на нахождение углов и расстояний в пространстве.
1. Цель работы
1. 1 Научиться решать задачи, применяя свойства параллельности прямых и плоскостей в пространстве
2. Ход работы
2.1. Вариант
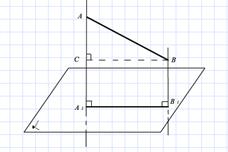
2.1.1 Через точки А и В проведены прямые, перпендикулярные плоскости α, пересекающие её в точках А1 и В1 соответственно. Найдите _________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
если отрезок АВ не пересекает плоскость α.
2.1.2 Из точки А проведена к плоскости α наклонная АС. Найти синус угла наклона касательной к плоскости α, если ________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.3 Прямые АВ, АС, АД попарно перпендикулярны. Найдите __________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.4 Через вершину квадрата АВСД проведена прямая ВО, перпендикулярная его плоскости. Найдите___________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.5.Из точки А к плоскости проведены две наклонные АВ и АС. Найдите ________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.6 Две плоскости пересекаются под углом α.. Найти cosα, если ________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.7 Точка Д равноудалена от вершин равностороннего треугольника АВС. Найти
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.8 Точка Д равноудалена от сторон равностороннего треугольника АВС. Найдите
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.2. Допуск к работе
2.2.1  Запишите теорему Пифагора для треугольника АВС
Запишите теорему Пифагора для треугольника АВС
2.2.2 Запишите формулу для вычисления синуса и косинуса угла АСВ
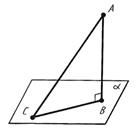
sin ACB = 
cos ACB = 
2.2.3 Запишите формулы для вычисления радиуса вписанной и описанной
окружности правильного треугольника
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
 |
2.2.4 Через вершину квадрата АВСД проведена прямая ВО, перпендикулярная его
плоскости. Выпишите все прямоугольные треугольники, изображённые на
рисунке и укажите какой угол у них прямой.
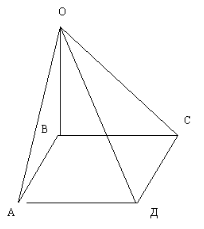
____________________________
____________________________
____________________________
____________________________
2.2.5 Сформулируйте свойство точки равноудалённой от вершин многоугольника
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
2.2.6 Сформулируйте свойство точки равноудалённой от сторон многоугольника
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
К работе допускается ______________
3. Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 21
Координаты и вектора в пространстве.
1. Цель работы
1. 1 Научиться выполнять действия над векторами, заданными своими координатами
2. Ход работы
2.1. Вариант
2.1.1 Построить параллелепипед АВСДА1В1С1Д1, пользуясь правилом треугольника или правилом параллелограмма, найти вектор, равный сумме векторов __________________________________
2.1.2 Треугольник АВС задан координатами своих вершин
________________________________________________________________
Найти: а) периметр треугольника АВС
б) косинус угла между сторонами ____________________________
в) длину медианы _____
г) длину средней линии ____ || ____
д) координаты точки пересечения медиан
е) считая, что точки А, В, С – три вершины параллелограмма,
найти координаты четвёртой вершины.
2.1.3 Даны вектора:
________________________________________________________________
Найти: а) скалярное произведение векторов 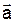 и
и 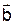
б) координаты вектора _____________________________________
в) скалярный квадрат вектора _______________________________
г) проекцию вектора ____ на вектор _____
д) модуль вектора ______
е) найти координаты точки М, если N(_________) и 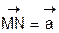
2.1.4 При каком значении m вектора _____________________________________
будут перпендикулярны?
2.1.5 При каком значении k и n вектора __________________________________
будут коллинеарными?
2.2. Допуск к работе
2.2.1  Пусть известны координаты точек А(ха; уа; za) и В(хb; уb; zb). Запишите формулы для вычисления:
Пусть известны координаты точек А(ха; уа; za) и В(хb; уb; zb). Запишите формулы для вычисления:
А) Координат вектора 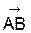 _______________________________________
_______________________________________
Б) Расстояния АВ ______________________________________________
2.2.2  Пусть известны координаты векторов
Пусть известны координаты векторов 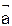 (ах; ау; аz) и
(ах; ау; аz) и 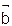 (bx; by; bz). Запишите формулы для вычисления:
(bx; by; bz). Запишите формулы для вычисления:
A) Координат вектора 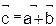 ___________________________________
___________________________________
Б) Координат вектора 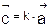 ___________________________________
___________________________________
 В) Скалярного произведения векторов
В) Скалярного произведения векторов 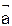 и
и 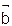 ________________________
________________________
Г) Скалярного квадрата вектора 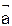 _________________________________
_________________________________
Д) Проекции вектора 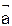 на вектор
на вектор 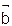 ________________________________
________________________________
2.2.3 Запишите условие параллельности векторов 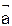 и
и 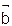 , заданных своими координатами._________________________________________________________________________________________________
, заданных своими координатами._________________________________________________________________________________________________
2.2.4 Запишите условие перпендикулярности векторов 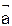 и
и 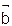 , заданных своими координатами. __________________________________
, заданных своими координатами. __________________________________
_______________________________________________________
К работе допускается ______________
3. Результаты работы
 ПРАКТИЧЕСКАЯ РАБОТА 22
ПРАКТИЧЕСКАЯ РАБОТА 22
Нахождение основных элементов призм.
1. Цель работы
1. 1 Научиться изображать призму и находить длину основных элементов, используя определение и свойства призм
2. Ход работы
2.1. Вариант
2.1.1 Сделайте рисунок
_____________________________________________________________ обозначьте её и запишите:
- вершины,
- основания,
- боковые рёбра,
- боковые грани,
- проведите одну из диагоналей её боковой грани и выпишите её,
- проведите две диагонали призмы и выпишите их,
- постройте одно диагональное сечение и выпишите его.
2.1.2 ___________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.3 В правильной четырехугольной призме ________________________________
____________________________________________________________________
Дата добавления: 2015-08-10; просмотров: 74 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| 2 страница | | | 4 страница |