
|
Читайте также: |
2. Ход работы
2.1. Вариант
2.1.1 Решите уравнения:
2.1.1.1.
2.1.1.2.
2.1.1.3
2.1.1.4
2.1.1.5
2.1.2. Решите неравенства:
2.1.2.1.
2.1.2.2.
2.1.2.3
2.1.2.4
2.1.2.5
2.2  Допуск к работе
Допуск к работе
2.2.1 Представьте в виде логарифма с основанием 2:
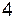 = =
|  = =
| 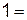
|
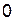 = =
|  = =
| 
|
2.2.2 Укажите вид монотонности функции y = log a x в зависимости от значения а.
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.2.3 Закончите схему:
 |

 log a f(x) > log a g(x)
log a f(x) > log a g(x)
 |  |
a > 1 0 < a < 1
f(x) g(x) f(x) g(x)
f(x) f(x)
g(x) g(x)
К работе допускается ______________
3. Результаты работы
 ПРАКТИЧЕСКАЯ РАБОТА 9
ПРАКТИЧЕСКАЯ РАБОТА 9
Выполнение тождественных преобразований тригонометрических выражений.
1. Цель работы
1. 1 Научиться преобразовывать тригонометрические выражения и вычислять значения тригонометрических функций, используя основные тригонометрические формулы
2. Ход работы
2.1. Вариант
Вычислите:
2.1.1.
2.1.2
Упростите:
2.1.3
Известно, что х =  и < x <. Вычислить:
и < x <. Вычислить:
2.1.4
2.1.5
2.1.6
2.1.7
Упростите:
2.1.8
Вычислите:
2.1.9.
Упростите:
2.11
2.11
2.2.  Допуск к работе
Допуск к работе
2.2.1. Заполните таблицу:
 (в радианах)
(в радианах)
| 
| 
| 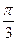
| 
| 
| 
| 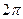
| |
 (в градусах) (в градусах)
| ||||||||

| ||||||||

| ||||||||

| ||||||||
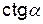
|
2.2.2 Заполните схему


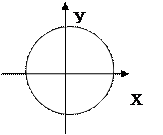

Знаки синуса Знаки косинуса Знаки тангенса
2.2.3 Продолжите равенства:

| 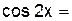
| 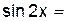
|

| 
| 
|
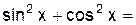
| 
| 
|

| ||

| ||
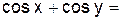
| ||

| ||

| ||
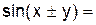
| ||
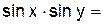
| ||
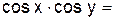
| ||

|
К работе допускается ______________
3. Результаты работы
 |
Построение графиков тригонометрических функций.
1. Цель работы
1. 1 Научиться строить графики тригонометрических функций и выполнять преобразование графиков
2. Ход работы
2.1. Вариант
Постройте графики функций:
| 2.1.1. | 2.1.3 |
| 2.1.2 | 2.1.4 |
| 2.1.5 |
 2.2. Допуск к работе
2.2. Допуск к работе
2.1.1. Вычислите:

| 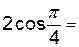
| 
|

| 
| 
|

| 
| 
|
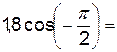
| 
| 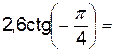
|
2.2.2 При построении графиков тригонометрических функций часто используют следующий масштаб: 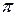 - 6 клеток. Заполните таблицу
- 6 клеток. Заполните таблицу
 (в радианах)
(в радианах)
| 
| 
| 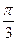
| 
| 
| 
| 
| |
| Клеток на графике |
К работе допускается ______________
3. Результаты работы
 |
Решение тригонометрических уравнений.
1. Цель работы
1. 1 Научиться решать простейшие тригонометрические уравнения;
1.2 Научиться решать тригонометрические уравнения, приводимые к простейшим;
1.3 Научиться решать однородные тригонометрические уравнения первой и второй степени.
2. Ход работы
2.1. Вариант
Решите уравнения:
| 2.1.1. | 2.1.6. |
| 2.1.2 | 2.1.7 |
| 2.1.3 | 2.1.8 |
| 2.1.4 | 2.1.9 |
| 2.1.5 | 2.1.10 |
 2.2. Допуск к работе
2.2. Допуск к работе
2.2.1 Заполните таблицу:
| Уравнение | Решение уравнения |
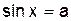
| |

| |

| |

|
2.2.2 Вычислите:

| 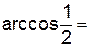
| 
|

| 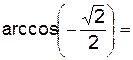
| 
|
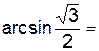
| 
| 
|

| 
| 
|
К работе допускается ______________
3. Результаты работы
 |
 ПРАКТИЧЕСКАЯ РАБОТА 12
ПРАКТИЧЕСКАЯ РАБОТА 12
Последовательности. Способы задания и свойства числовых последовательностей.
1. Цель работы
1.1 Научиться вычислять n-ые члены последовательностей, заданных различными способами;
1.2 Научиться изображать последовательности различными способами;
1.3 Научиться использовать формулу суммы геометрической прогрессии для решения задач
1.3 Научиться вычислять пределы числовых последовательностей.
2. Ход работы
2.1. Вариант
2.1.1 Найдите первые пять членов последовательности yn = 
2.1.2 Найдите минимальный отрезок [m;M] с целочисленными m и M, которому принадлежат все члены последовательности хn = 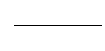 .
.
2.1.3 Первые четыре члена последовательности аn = отметьте на оси ОХ и укажите характер монотонности.
2.1.4 Выясните, является ли число b членом последовательности bn и укажите номер n
bn =  , b=
, b=
2.1.5 Вычислите пределы
А) 
| Б) 
|
В) 
| Г) 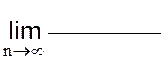
|
Д) 
| Е) 
|
 2.2. Допуск к работе
2.2. Допуск к работе
2.2.1. Дайте определение числовой последовательности
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.2.2. Перечислите способы задания последовательностей
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.2.3. Укажите нижнюю границу последовательности 4,5.6,…,n+3,…
________________________________________________________________________________________________________________________________________________
2.2.4. Укажите верхнюю границу последовательности -6,-7, -8, …, - n - 5
________________________________________________________________________________________________________________________________________________
2.2.5. Запишите формулу для вычисления суммы геометрической прогрессии, если 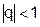
________________________________________________________________________________________________________________________________________________
________________________________________________________________________
2.2.6 Продолжите равенства:

| 
| 
| 
|
Если 
 , то
, то
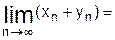
| 
|

| 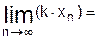
|
К работе допускается ______________
3. Результаты работы
 |
ПРАКТИЧЕСКАЯ РАБОТА 13
Нахождение производных функции.
1. Цель работы
1. 1 Научиться вычислять производную функции, используя таблицу производных и правила дифференцирования;
2. Ход работы
2.1. Вариант
Вычислите производную:
| 2.1.1. | 2.1.11 |
| 2.1.2 | 2.1.12 |
| 2.1.3 | 2.1.13 |
| 2.1.4 | 2.1.14 |
| 2.1.5 | 2.1.15 |
| 2.1.6 | 2.1.16 |
| 2.1.7 | 2.1.17 |
| 2.1.8 | 2.1.18 |
| 2.1.9 | 2.1.19 |
| 2.1.10 | 2.1.20 |
 2.2. Допуск к работе
2.2. Допуск к работе
2.2.1 Заполните таблицу производных:

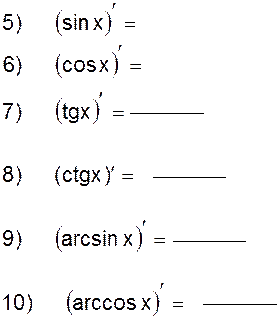
| 

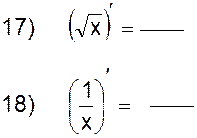
|
2.2.2 Допишите равенства:
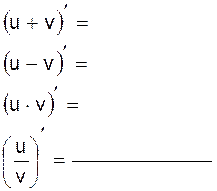

|
К работе допускается ______________
3. Результаты работы
 |
ПРАКТИЧЕСКАЯ РАБОТА 14
Построение графиков функции с помощью производной.
1. Цель работы
1. 1 Научиться исследовать функцию с помощью производной и строить по результатам исследования график
2. Ход работы
2.1. Вариант
Исследовать функцию и построить её график:
2.1.1
2.1.2
2.1.3
2.1.4
 2.2. Допуск к работе
2.2. Допуск к работе
2.2.1 Заполните пропуски
А) Если производная дифференцируемой функции положительна на промежутке, то функция на этом промежутке _____________________.
Б) Если производная дифференцированной функции _________________ на промежутке, то функция на этом промежутке убывает.
В) Если для дважды дифференцируемой функции вторая её производная отрицательна внутри промежутка, то график функции является ______________ на данном промежутке.
Г) Если же вторая производная __________________ внутри промежутка, то график функции является вогнутым на данном промежутке.
3.2.1 Заполните пропуски
Схема исследования функции
1. Найдите область определения функции.
2. Определите четность, нечетность функции. (f(-x) = f(x) - ____________________
f(-x) = __________ - нечётная)
4 Найти точки пересечения график функции с осями координат. (с осью ОХ у = ___, с осью _____ х = 0).
4. Найдите производную функции.
5. Определите стационарные и критические точки производной. Т. е. точки в которых производная равна ________ и не существует.
 |  |

7. Найдите значения функции в _________________________ и критических точках.
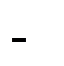 |

9. Для построения графика найдите необходимые дополнительные точки.
2.2.3 Дорисуйте схемы
 А) Б)
А) Б)
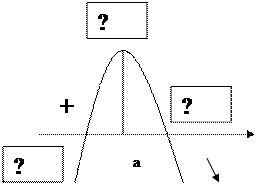
К работе допускается ______________
3. Результаты работы
 |
 ПРАКТИЧЕСКАЯ РАБОТА 15
ПРАКТИЧЕСКАЯ РАБОТА 15
Применение производной для решения задач.
1. Цель работы
1. 1 Научиться применять производную для решения геометрических и физических задач
1.2 Научиться применять производную для приближённых вычислений
2. Ход работы
2.1. Вариант
2.1.1 Вычислить приближённо е
2.1.2. Найдите тангенс угла наклона к оси ОХ касательной графика функции

2.1.3 Написать уравнен6ие касательной к графику функции f(x)=
в точке с абсциссой х0 =
2.1.4 Материальная точка движется прямолинейно по закону
x(t) =
а) Записать формулы для вычисления скорости и ускорения движения
б) Найти скорость и ускорение в момент времени t =
в) Через сколько секунд после начала движения точка остановиться?
2.1.5 Найдите наибольшее и наименьшее значение функции f(x)=
на отрезке [; ]
2.1.6 Решите задачу:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Дата добавления: 2015-08-10; просмотров: 101 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| 1 страница | | | 3 страница |