Теоретические сведения. При подготовке к работе повторить материал учебника «Теоретические основы

При подготовке к работе повторить материал учебника «Теоретические основы электротехники», автор Лоторейчук Е.А., глава 14 «Символический метод расчета электрических цепей переменного тока».

Символический метод расчета основан на использовании комплексных чисел. Комплексное число А состоит из вещественной А^' и мнимой частей А^''

А = А^'+ jА^''

Комплексное число А на комплексной плоскости можно представить вектором.

Проекция вектора на вещественную ось (ось абсцисс) соответствует А^', а проекция на мнимую ось j (ось ординат) соответствует коэффициенту при мнимой единице А^''.

Мнимая единица j – это поворотный множитель, умножение на который означает поворот вектора на 90⁰ против часовой стрелки, т.е. в положительном направлении.

Комплексным числам А =3+j4 и В = -5-j2 соответствуют векторы и , изображенные на комплексной плоскости (рисунок 1) в масштабе.

Модуль комплексного числа – это длина вектора, изображающего данное число.

Угол α, образованный вектором , с положительным направлением вещественной оси называется аргументом комплексного числа. За положительное значение аргумента принимается поворот вектора против часовой стрелки относительно вещественной оси.

Рисунок 1 – Комплексная плоскость

Рисунок 2 – Действия над комплексными числами

Существует три формы записи комплексного числа.

Алгебраическая А = А^'+ jА^''

Тригонометрическая

Показательная

При переводе из показательной формы в алгебраическую используют тригонометрическую форму. При переводе из алгебраической формы в показательную, определяют модуль и аргумент числа.

Сложение и вычитание комплексных чисел выполняется в алгебраической форме, а умножение и деление в показательной.

Расчетные формулы:

А + В = А^'+ jА^'' + В^'+ jВ^''

А - В = А^' + jА^''– (В^' + jВ^'')

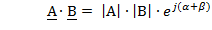
Пример

Рассчитать сумму, разность, частное, произведение двух комплексных чисел А и В. Построить векторы на комплексной плоскости. А = 3 + j4; В = 5 - j2.

Решение

Сумма и разность чисел А и В:

А + В = А^'+ jА^'' + В^'+ jВ^''= 3 +j4 + 5 - j2 = 8 + j2

А - В = А^' + jА^''– (В^' + jВ^'') = 3 +j4 – (5 - j2)

Модули чисел:

=

=

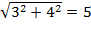
Аргументы чисел:

Показательная форма записи чисел:

Умножение и деление чисел:

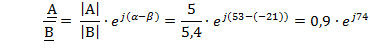
Векторы чисел А и В, а также векторы их суммы и разности представлены на рисунке 2.

Сумма векторов может быть найдена графическим способом по правилу параллелограмма.

Дата добавления: 2015-08-10