Теоретические сведения. При подготовке к работе повторить материал учебника «Теоретические основы

При подготовке к работе повторить материал учебника «Теоретические основы электротехники», автор Лоторейчук Е.А., глава 12 «Расчет линейных электрических цепей синусоидального тока».

В цепи с реальной (обладающей активным сопротивлением) катушкой на рисунке 1 а) уравнения токов и напряжений имеют вид:

i(t)=I_msinωt

u_R(t)=U_mRsinωt

u_L(t)=U_mLsin(ωt+90⁰)

Ток i создает падение напряжения на активном сопротивлении проводников катушки u_R и индуктивном сопротивлении катушки u_L. Активное напряжение совпадает по фазе с током, а индуктивное опережает ток на 90⁰. Мгновенное значение напряжения, приложенного к цепи с реальной катушкой, определяется алгебраической суммой мгновенных напряжений u_R и u_L. Действующее значение U определяется геометрической суммой векторов действующих значений U_R и U_L.

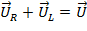
Рисунок 1 – RL - цепь

Из векторной диаграммы на рисунке 1 б) видно, что напряжение на зажимах цепи опережает ток на угол φ. Мгновенное значение этого напряжения:

u (t)=U_msin(ωt+φ),

где:

φ – международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.

Закон Ома для цепи с реальной катушкой:

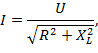
где:

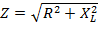- полное сопротивление RL - цепи.

В цепи с конденсатором на рисунке 2 а) уравнения токов и напряжений имеют вид:

i(t)=I_msinωt

u_R(t)=U_mRsinωt

u_с(t)=U_mсsin(ωt-90⁰)

Ток i создает падение напряжения на активном сопротивлении u_R и емкостном сопротивлении u_с. Активное напряжение совпадает по фазе с током, а емкостное отстает от тока на 90⁰. Мгновенное значение напряжения, приложенного к цепи с реальной катушкой, определяется алгебраической суммой мгновенных напряжений u_R и u_L. Действующее значение U определяется геометрической суммой векторов действующих значений U_R и U_L.

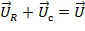
Из векторной диаграммы на рисунке 2 б) видно, что напряжение на зажимах цепи отстает от тока на угол φ. Мгновенное значение этого напряжения:

u (t)=U_msin(ωt-φ),

Рисунок 2 – RС - цепь

Закон Ома для цепи с емкостью:

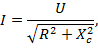
где

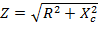- полное сопротивление RC - цепи.

Резонанс напряжений в RLC – цепи возникает, если X_L = X_c, тогда полное сопротивление цепи 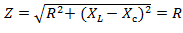становится минимальным, а ток увеличивается.

Рисунок 3 – RLC - цепь

Рисунок 4 – Векторные диаграммы RLC – цепи

а) X_L > X_c –индуктивный характер цепи;

б) X_L < X_c–емкостный характер цепи;

в) X_L = X_c – резонанс напряжений.

Мгновенное значение напряжения:

u (t)=U_msin(ωt±φ),

Закон Ома для RLC- цепи:

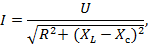
где

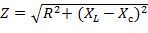- полное сопротивление RLС - цепи.

Полная мощность цепи переменного тока, ВА

S = U·I

Активная мощность цепи переменного тока, Вт

P = S·cosφ= U·I ·cosφ

Коэффициент мощности

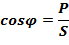
Реактивная мощность

Q = S·sinφ= U·I ·sinφ

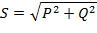
Пример

Закон изменения тока (t)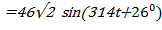

Определить полное сопротивление цепи; закон изменения приложенного напряжения; полную, активную, реактивную мощность. Построить векторную диаграмму. Рассчитать емкость конденсатора и индуктивность катушки. Определить характер цепи.

R₁ = 6 Ом; R₂= 5 Ом; X_L = 16 Ом; X_c = 9 Ом;

Решение

Полное сопротивление цепи

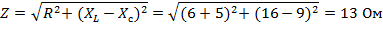
Амплитудное значение тока

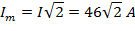
Действующее значение тока

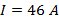
Действующее значение напряжения

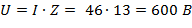
Амплитудное значение напряжения

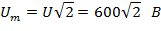
Угол сдвига фаз между током и напряжением

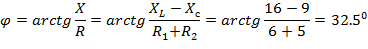
Закон изменения приложенного напряжения

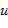(t)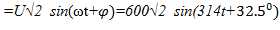

Характер цепи – индуктивный, т.к.знак + φ.

Напряжение на участках цепи

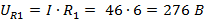
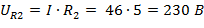
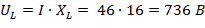
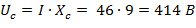
Полная мощность цепи переменного тока, ВА

S = U·I =600·46=27600 ВА

Активная мощность цепи переменного тока, Вт

P = S·cosφ= 27600 ·cos 32,5⁰=23277 Вт

Коэффициент мощности

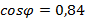
Реактивная мощность

Q = S·sinφ= 27600 ·sin32,5⁰=14829 вар

Емкость конденсатора и индуктивность катушки

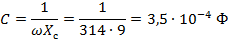
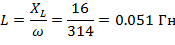
Резонансная частота

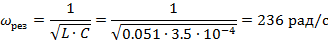
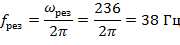
Ток в цепи при резонансе

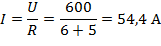
Условие резонанса X_L = X_c. По условию задачи X_L =16 Ом, а X_c=9 Ом. Этому X_c соответствует емкость С=3,5·10^-4 Ф. Для выполнения условия резонанса емкостное сопротивление надо увеличить до16 Ом. Тогда емкость будет уменьшена до С=2·10^-4 Ф.

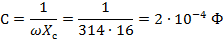
Рисунок 5- Векторная диаграмма

Задание

Для своего варианта рассчитать параметры однофазной цепи синусоидального тока.

Таблица 1 – Данные для расчета

вариант	1	2	3	4	5	6	7	8	9	10	11	12	13	14
I, А
f, Гц
φi, град	-30			-28		-60		-35		-64	-52			-50
R1, Ом			-		-					-
R2, Ом		-					-						-
XL1,Ом				-							-
XL2,Ом	-					-			-			-
Xc2,Ом								-
Xc2,Ом														-

Требуется определить:

1. закон изменения тока;

2. полное сопротивление цепи;

3. закон изменения приложенного напряжения;

4. характер цепи;

5. напряжение на участках цепи;

6. полную, активную, реактивную мощность;

7. построить векторную диаграмму;

8. емкость конденсатора и индуктивность катушки;

9. параметры резонанса напряжений – частоту, емкость, индуктивность, ток.

Контрольные вопросы

1. Как распределяется потребляемая мощность в RLC –цепи?__________________________

_____________________________________________________________________________

2. Как определить угловую частоту по закону изменения тока?_________________________

3. От чего зависит величина индуктивности?________________________________________

4. Как меняется емкостное сопротивление при увеличении частоты тока?________________

5. Чем опасен резонанс напряжений в цепи?

Практическая работа №14

ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ

Цели: 1. Повторить теоретический материал.

2. Освоить расчет электрических цепей переменного тока символическим методом.

3. Построить векторную диаграмму.

Необходимо знать: комплексная плоскость, мнимая, действительная часть, тригонометрическая и показательная форма.

Необходимо уметь: определять: характер цепи.

Оборудование: калькулятор с комплексными числами, конспект лекций, учебник

Порядок работы:

Дата добавления: 2015-08-10