Повторить теоретический материал

Теоретические сведения

При подготовке к работе повторить материал учебника «Теоретические основы электротехники», автор Лоторейчук Е.А., глава 4 «Методы расчета электрических цепей».

Сложная электрическая цепь – это такая цепь, в которой несколько источников и резисторов включены смешано.

Чтобы решить сложную электрическую цепь вначале нужно определить, сколько в ней узлов, сколько ветвей, сколько замкнутых контуров.

В каждой ветви нужно показать направление тока и обозначить его. В сложной электрической цепи направление тока показывается произвольно, каждый ток течет от узла до узла.

Если направление тока не угадали, он при решении получается со знаком (-).

Для решения сложных электрических цепей существует несколько методов:

1. метод наложения;

2. законы Кирхгофа – метод узловых и контурных уравнений;

3. метод контурных токов;

4. метод узловых потенциалов;

5. метод эквивалентного генератора.

Пример

А

В

I_A

I_B

E₁

E₂

r₁

r₂

R₁

I₁

I₂

R₂

I₃

R₃

Рисунок 1 – Электрическая цепь с двумя источниками ЭДС

Определить токи I₁, I₂, I₃ в ветвях сложной цепи постоянного тока, если известны значения ЭДС Е₁, Е₂, r₁, r₂ и сопротивлений резисторов R₁, R₂, R₃ методом наложения.

Решение

Данная схема представляет собой сложную электрическую цепь. В схеме два узла А и В; три ветви, в которых текут токи I₁, I₂, I₃; три замкнутых контура.

А

В

E₁

r₁

r₂

R₁

R₂

R₃

а)

А

В

E₁

r₁

R₂₂₃

R₁

б)

Рисунок 2 – Преобразование электрической цепи

а) с одним источником ЭДС Е₁

б) с последовательным соединением резисторов

Согласно методу наложения ток в каждой ветви определяется как алгебраическая сумма частичных токов определенных от каждой ЭДС в отдельности.

Ø E₂ = 0, а сопротивление r₂ существует рисунок 2- а).

Получили простую электрическую цепь с одной ЭДС Е₁. В простой электрической цепи направление тока совпадают с направлением ЭДС. Токи текут под действием только одной ЭДС, поэтому они частичные.

R₂₂ = r₂ + R₂

Получили простую электрическую цепь, в которой три резистора r₁, R₁ и R₂₂₃ включены последовательно - рисунок 2 - б).

Ø E₁ = 0, а сопротивление r₁ остается, рисунок 3 - а).

R₁₁ = r₁ + R₁

А

В

r₁

r₂

R₁

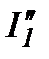
R₂

R₃

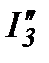
Е₂

а)

А

В

E₂

r₂

R₁₁₃

R₂

б)

Рисунок 3 – Преобразование электрической цепи

а) с одним источником ЭДС Е₂

б) с последовательным соединением резисторов

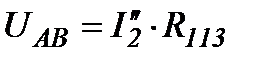
Реальные токи в сложной электрической цепи определяются, как их сумма частичных токов:

Ток берем со знаком (+), так как его направление совпадает с направлением тока I₁; ток берем со знаком (-), так как его направление встречно направлению тока I₁.

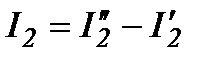
Метод узловых и контурных уравнений. Решая этим методом нужно составить всего столько уравнений сколько в схеме неизвестных токов. В данной схеме 3 неизвестных тока – I₁, I₂, I₃ (рисунок 1).

Сначала составляются узловые уравнения по I закону Кирхгофа. Их составляется на одно меньше, чем узлов. I закон Кирхгофа – сумма токов, приходящих в узел, равна сумме токов, выходящих из узла. Для данной схемы надо составить одно узловое уравнение, так как в схеме всего 2 узла.

Остальные уравнения (в данной схеме их 2) составляются по II закону Кирхгофа. II закон Кирхгофа – в замкнутом контуре алгебраическая сумма э.д.с. равна алгебраической сумме падений напряжений.

I₁ + I₂ = I₃

E₁ – E₂ = I₁ · (R₁ + r₁) – I₂ · (R₂ + r₂)

E₂ = I₂ · (R₂ + r₂) + I₃R₃

Решая данную систему уравнений определим токи I₁, I₂, I₃.

Метод контурных токов. Контурный ток – это расчетный реально не существующий ток, замыкающийся по простейшему контуру электрический цепи.

В данной электрической цепи два простейших контура, через которые замыкаются контурные токи – I_A и I_B.

Решая методом контурных токов уравнения составляются только по II закону Кирхгофа (рисунок 1).

Е₁ – Е₂ = I_A · (r₁ + R₁ + r₂ + R₂) – I_B · (R₂ + r₂)

E₂ = I_B · (R₂ + r₂ + R₃) – I_A · (R₂ + r₂)

Решая эту систему уравнений определим контурные токи - I_A и I_B.

Реальные токи в электрической цепи:

I₁ = I_A

I₂ = I_B - I_A

I₃ = I_B

Метод узловых потенциалов. Решая этим методом, составляется уравнение для одного узла, в котором ток ветвей выражается через потенциалы и проводимости.

φ_В · (q₁ + q₂ + q₃) – φ_A · (q₁ + q₂ + q₃) = - E₁q₁ – E₂q₂,

где

q₁, q₂, q₃ – проводимости ветвей.

; ;

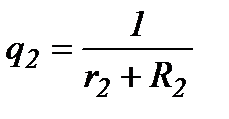Пусть φ_А = 0.

Если ЭДС направлена от узла, она берется со знаком (-).

φ_B · (q₁ + q₂ + q₃) = - E₁q₁ – E₂q₂

Из этого уравнения определяем φ_В, затем определяем токи.

---

Дата добавления: 2015-08-10