
Читайте также:
|
Общее количество неповторяющихся сообщений, которое может быть
составлено из алфавита m, путём комбинирования по n символов в
сообщении:
N = mn (1)
Неопределённость, приходящаяся на символ первичного
(кодируемого) алфавита, составленного из равновероятностных и
взаимонезависимых символов:
H = log2 m (2)
Так как информация есть неопределённость, снимаемая при
получении сообщения, то количество информации может быть представлено как произведение общего числа сообщений k на среднюю энтропию H, приходящуюся на одно сообщение:
I=k  H бит (3)
H бит (3)
Для случаев равновероятностных и взаимонезависимых символов
первичного алфавита количество информации в k сообщениях алфавита m
равно:
I= k  log2 m бит (4)
log2 m бит (4)
Для неравновероятностных алфавитов энтропия на символ алфавита
составляет:
H =  log2
log2 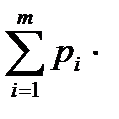
 =
= 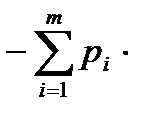 log2 pi бит/символ (5)
log2 pi бит/символ (5)
А количество информации в сообщении, составленном из k
неравновероятностных символов:
I=  k
k  log2 pi бит (6)
log2 pi бит (6)
Количество информации определяется исключительно
характеристиками первичного алфавита, объём — характеристиками
вторичного алфавита. Объём информации может быть вычислен следующим образом:
Q = k  lср (7)
lср (7)
Где l ср — средняя длина кодовых слов вторичного алфавита.
Для равномерных кодов (когда все комбинации кода содержат
одинаковое количество разрядов), количество информации может быть
определено следующим образом:
Q = k  n (8)
n (8)
Где n — длина кода (число элементарных посылок в коде).
Дата добавления: 2015-08-10; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теоретическая часть | | | Способности каналов связи |