Теоретическая часть. В данной расчётно-графической работе рассматривается алфавит из

Аннотация

В данной расчётно-графической работе рассматривается алфавит из

символов, появляющихся с определённой вероятностью, для которого

рассчитаны различные величины: количество информации, приходящееся насимвол сообщения в случае равновероятных и неравновероятныхсимволов,недогруженность символов, скорость передачи данных и т. д.

Также для данного алфавита выполняется построение оптимального двоичного кода на основе методик Шеннона – Фано и Хаффмана.

В процессе выполнения данной расчётно-графической работы

происходит закрепление знаний, полученных при освоении дисциплины

«Информационные технологии».

Содержание задания

Исходные данные для выполнения расчётно-графической работы

индивидуальны и определяются на основе значения переменной λ,

указанного в задании на расчётно-графическую работу.

Для выполнения расчётов предполагается использование

демонстрационной версии интегрированной среды выполнения

инженерных расчётов PTC Mathcad или разработка прикладной программы

средствами одного из современных языков программирования высокого

уровня.

Число символов алфавита k = λ + 7.

Необходимо определить количество информации, соответствующее

одному символу сообщения, составленного из данного алфавита:

a) если символы алфавита встречаются с равными вероятностями;

b) если символы алфавита встречаются в сообщении с

вероятностями:

p₁= ;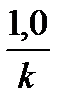

p₂ = 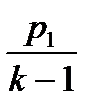; p₃ =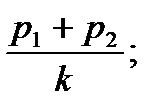

p_n-1= 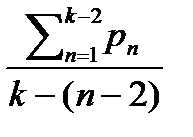; p_n= .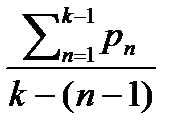

Определить, насколько недогружены символы во втором случае.

Число символов алфавита равно k. Вероятности появления символов равны соответственно:

Длительности символов: τ₁ = 1 с; τ₂ = 2 с; τ _k-1 = τ _k-1 + 1.

Чему равна теоретическая скорость передачи сообщений,

составленных из таких символов?

Cообщения составляются из алфавита с числом символов, равным k.

Вероятность появления символов алфавита равна соответственно:

p₂ = 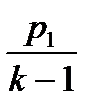; p₃ =

p_n-1= ; p_n= .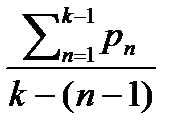

Найти избыточность сообщений, составленных из данного алфавита.

Построить оптимальный код сообщения.

Теоретическая часть

Дата добавления: 2015-08-10