Задача 2.

Рассмотрим задачу с применением "дерева" решений.

Ограниченность непрерывных на отрезке функций Пример. Показать, что на интервале непрерывная функция может быть неограниченной и не достигать верхней (нижней) грани.

Выбор оптимальной стратегии развития предприятия в условиях трансформации рынка

Фирма может принять решение о строительстве среднего или малого предприятия. Малое предприятие впоследствии можно расширить. Решение определяется будущим спросом на продукцию, которую предполагается выпускать на сооружаемом предприятии. Строительство среднего предприятия экономически оправданно при высоком спросе. С другой стороны, можно построить малое предприятие и через два года его расширить.

Фирма рассматривает данную задачу на десятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого и низкого уровней спроса равны 0,7 и 0,3 соответственно. Строительство среднего предприятия обойдется в 4 млн р., малого — в 1 млн р. Затраты на расширение через два года малого предприятия оцениваются в 3,5 млн р.

Ожидаемые ежегодные доходы для каждой из возможных альтернатив:

среднее предприятие при высоком (низком) спросе дает 0,9 (0,2) млн р.;

малое предприятие при низком спросе дает 0,1 млн р.;

малое предприятие при высоком спросе дает 0,2 млн р. в течение 10 лет;

расширенное предприятие при высоком (низком) спросе дает 0,8 (0,1) млн р.;

малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает 0,1 млн р. в год за остальные восемь лет.

Определить оптимальную стратегию фирмы в строительстве предприятий.

Решение. Данная задача является многоэтапной, так как если фирма решит строить малое предприятие, то через два года она может принять решение о его расширении. В этом случае процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о размере предприятия и решение о необходимости его расширения, принимаемое через два года.

На рис. 31.7 задача представлена в виде "дерева" решений. Предполагается, что спрос может оказаться высоким и низким. Дерево имеет два типа вершин: "решающие" вершины, обозначенные квадратными узлами, и "случайные" вершины, обозначенные круглыми узлами.

Начиная с вершины 1, являющейся "решающей", необходимо принять решение относительно размера предприятия. Вершины 2 и 3 являются "случайными". Фирма будет рассматривать возможность расширения малого предприятия только в том случае, если спрос по истечении первых двух лет установится на высоком уровне. Поэтому в вершине 4 принимается решение о расширении или нерасширении предприятия.

Вершины 5 и 6 будут "случайными".

Произведем расчеты для каждой из альтернатив. Вычисления начнем со 2-го этапа. Для последних восьми лет альтернативы, относящиеся к вершине 4, оцениваются так:

где ДР — доход с расширением, ДБР — доход без расширения предприятия.

Таким образом, в вершине 4 выгоднее не проводить расширение, при этом доход составит l,36 млн р.

Теперь для дальнейших расчетов оставим одну "ветвь", выходящую из вершины 4, которой соответствует доход 1,36 млн р. за остальные восемь лет. Перейдем к вычислениям 1-го этапа. Для вершины 1

где ДС — доход среднего предприятия, ДМ — доход малого предприятия.

Сравнивая получаемые в вершине 1 доходы среднего и малого предприятий, видим, что более предпочтительным является вариант строительства среднего предприятия.

Таким образом, фирме целесообразно построить среднее предприятие.

Принятие решения о замене оборудования в условиях неопределенности и риска

Фирма может принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.

Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.

Полная замена оборудования экономически оправданна при высоком уровне спроса. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.

В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.

Пример 5. Рассмотрим конкретную задачу о замене оборудования фирмы, представленную в виде "дерева" решений.

Предполагается, что спрос может оказаться высоким, средним и низким.

Дерево имеет два типа вершин: "решающие" и "случайные".

Начиная с "решающей" вершины 1 необходимо принять решение о полной замене оборудования или его ремонте.

Вершины 2 и 3 являются "случайными". Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 "случайные".

Предположим, что фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют 0,6, 0,3 и 0,1 соответственно. Замена новым оборудованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого — в 0,8 млн р.

Затраты на частичную замену оборудования на более совершенное, чем старое, оцениваются в 1,5 млн р., а повторный ремонт старого — в 0,8 млн р.

Ежегодные доходы для каждой стратегии фирмы следующие.

1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса дает 0,95; 0,7 и 0,45 млн р. соответственно.

2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается в 0,3; 0,15 и 0,1 млн р. соответственно.

3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит 0,9; 0,6 и 0,4 млн р. соответственно.

4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает 0,3; 0,2 и 0,1 млн р. соответственно.

Определить оптимальную стратегию фирмы в замене оборудования.

Решение. Оценим результаты каждой стратегии и определим, какие решения следует принимать в "решающих" вершинах 1 и 4.

Вычисления начнем с этапа 2. Для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:

где ДЧЗ — доход от частичной замены оборудования на более совершенное, ДДР — доход от замены оборудования, прошедшего дважды ремонт. Так как ДЧЗ > ДДР, то в вершине 4 выгоднее произвести частичную замену оборудования на более совершенное, при этом доход составит 1,54 млн р.

Для дальнейших расчетов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 1,54 млн р. за 4 года.

Вычислим доходы на 1-м этапе для "решающей" вершины 1:

где ДЗН — доход от замены старого оборудования на новое того же вида, ДЗО — доход от отремонтированного оборудования и дальнейшей замены на более совершенное.

Так как ДЗН > ДЗО, то оптимальным решением в вершине 1 является полная замена старого оборудования на новое того же вида.

Ответ: Оптимальной стратегией фирмы в замене оборудования является полная замена старого оборудования на новое того же вида, при этом доход составит 1,625 млн р.

Пример 1. Главному инженеру компании надо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного инженера, существует 60% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн. рублей. Главный инженер считает, что существует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов зато, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения?

Рисунок 1 (нажмите для увеличения).

В узле F возможны исходы «линия работает» с вероятностью 0,4 (что приносит прибыль 200) и «линия не работает» с вероятностью 0,6 (что приносит убыток - 150) => оценка узла F. EMV(F) = 0,4 x 200 + 0,6 х (-150) = -10. Это число мы пишем над узлом F.

EMV(G) = 0.

В узле 4 мы выбираем между решением «монтируем линию» (оценка этого решения EMV(F) = -10) и решением «не монтируем линию» (оценка этого решения EMV(G) = 0): EMV(4) = max {EMV(F), EMV(G)} = max {-10, 0} = 0 = EMV(G). Эту оценку мы пишем над узлом 4, а решение «монтируем линию» отбрасываем и зачеркиваем.

Аналогично:

EMV(B) = 0,9 х 200 + 0,1 х (-150) = 180 - 15 = 165.

EMV(С) = 0.

EMV(2) = max {EMV(В), EMV(С} = max {165, 0} = 165 = EMV(5). Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию».

EMV(D) = 0,2 х 200 + 0,8 х (-150) = 40 — 120 = -80.

EMV(E) = 0.

EMV(3) = max {EMV(D), EMV(E)} = max {-80, 0} = 0 = EMV(E). Поэтому в узле 3 отбрасываем возможное решение «монтируем линию».

ЕМV(A) = 0,5 х 165 + 0,5 х 0 — 10 = 72,5.

EMV(l) = max {EMV(A), EMV(4)} = max {72,5; 0} = 72,5 = EMV(A). Поэтому в узле 1 отбрасываем возможное решение «не строим установку».

Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не надо.

Пример 2. Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий.

A. Построить большой завод стоимостью M₁ = 700 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере R₁ = 280 тысяч долларов в течение следующих 5 лет) с вероятностью p₁ = 0,8 и низкий спрос (ежегодные убытки R₂ = 80 тысяч долларов) с вероятностью р₂ = 0,2.

Б. Построить маленький завод стоимостью М₂ = 300 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере T₁ = 180 тысяч долларов в течение следующих 5 лет) с вероятностью p₁= 0,8 и низкий спрос (ежегодные убытки Т₂ = 55 тысяч долларов) с вероятностью р₂ = 0,2.

B. Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p₃ = 0,7 и p₄= 0,3 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на p₅ = 0,9 и р₆ = 0,1 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет.

Все расчеты выражены в текущих ценах и не должны дисконтироваться. Нарисовав дерево решений, определим наиболее эффективную последовательность действий, основываясь на ожидаемых доходах.

Рисунок 2 (нажмите для увеличения).

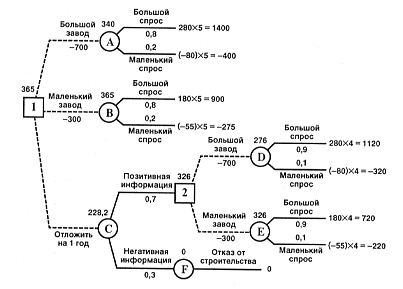
Ожидаемая стоимостная оценка узла А равна ЕМV(А) = 0,8 х 1400 + 0,2 х (-400) — 700 = 340.

EMV(B) = 0,8 х 900 + 0,2 х (-275) — 300 = 365.

EMV(D) = 0,9 x 1120 + 0,1 x (-320) — 700 = 276.

EMV(E) = 0,9 x 720 + 0,1 х (-220) — 300 = 326.

EMV(2) = max {EMV(D), EMV(E)} = max {276, 326} = 326 = EMV(E). Поэтому в узле 2 отбрасываем возможное решение «большой завод».

EMV(C) = 0,7 x 326 + 0,3 x 0 = 228,2.

EMV(1) = max {ЕМV(A), EMV(B), EMV(C)} = max {340; 365; 228,2} = 365 = EMV(B). Поэтому в узле 1 выбираем решение «маленький завод». Исследование проводить не нужно. Строим маленький завод. Ожидаемая стоимостная оценка этого наилучшего решения равна 365 тысяч долларов.

Задание 1. Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий.

A. Построить большой завод стоимостью M₁, = 650 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере R₁ = 300 тысяч долларов в течение следующих 5 лет) с вероятностью р₁ = 0,7 и низкий спрос (ежегодные убытки R₂ = 85 тысяч долларов) с вероятностью p₂ = 0,3.

Б. Построить маленький завод стоимостью М₂ = 360 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере T₁, = 120 тысяч долларов в течение следующих 5 лет) с вероятностью р₁ = 0,7 и низкий спрос (ежегодные убытки Т₂ = 60 тысяч долларов) с вероятностью р₂ = 0,3.

B. Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью р₃ = 0,9 и р₄ = 0,1 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на р₅ = 0,8 и р₆ = 0,2 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет.

Все расчеты выражены в текущих ценах и не должны дисконтироваться. Попробуйте самостоятельно нарисовать дерево решений и определить наиболее эффективную последовательность действий, основываясь на ожидаемых доходах. Какова ожидаемая стоимостная оценка наилучшего решения?

Вы можете проверить правильность выполнения задания, выделив мышью следующую строку. В ней ответ написан белым шрифтом на белом фоне.

Ответ здесь: Нужно строить большой завод. 272,5 тысяч долларов.

Дата добавления: 2015-08-10