Властивості дисперсії.

1. Якщо всі варіанти зменшити або збільшити на будь – яке постійне число , то середній квадрат відхилень від цього не зміниться.

Це означає, що дисперсію можна обчислювати не тільки за варіантами, а й за їх відхиленнями від деякого постійного числа.

2. Якщо всі варіанти зменшити або збільшити в разів, то дисперсія від цього зміниться в разів, а середнє квадратичне відхилення - в разів:

.

Отже, всі варіанти можна поділити на будь – яке постійне число (наприклад, на величину інтервалу ряду розподілу), розрахувати середнє квадратичне відхилення, а потім помножити його на постійне число:

;

3. Якщо розрахувати середній квадрат відхилень від довільної величини , яка відрізняється від середньої арифметичної , то він завжди буде більший за середній квадрат відхилень, обчислений від середньої арифметичної:

.

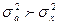При цьому середній квадрат відхилень означень ознаки 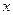від довільної величини завжди більший за дисперсію ознаки 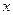на квадрат різниці між середньою арифметичною і довільною величинами:

З наведених формул видно, що дисперсія від середньої завжди менша за дисперсії, розраховані від будь – яких інших величин, тобто вона має властивість мінімальності.

Якщо довільну величину прирівняти до нуля, то попередня формула матиме такий вигляд:

Для перевірки першої властивості від усіх значень варіант віднімемо постійну величину, а (значення варіанти, що має найбільшу частоту) Тоді, з нових варіант обчислюємо середню арифметичну та дисперсію. Отримуємо таке ж значення, отже властивість справджується.

4. Дисперсія постійної величини дорівнює 0, бо немає варіації.

.

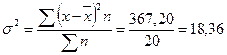Таблиця. Вихідні та розрахункові дані для вивчення математичних властивостей дисперсії

Урожайність зернових, ц/га	Кількість господарств,	Середина інтервалу,	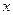Розрахункові дані
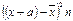
18 – 22					-6,2	38,44	153,76
22 – 26					-2,2	4,84	29,04
26 – 30					1,8	3,24	16,20
30 – 34					5,8	33,64	168,20
Разом		Х	Х		Х	Х	367,20

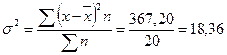
Таблиця. Вихідні та розрахункові дані для вивчення математичних властивостей дисперсії

Урожайність зернових,, ц/га	Кількість господарств,	Середина інтервалу,	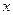Розрахункові дані
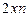
18 – 22					-12,4	153,76	615,04
22 – 26					-4,4	19,36	116,16
26 – 30					3,6	12,96	64,80
30 – 34					11,6	134,56	672,80
Разом		Х	Х		Х	Х	1468,80

;

;

.

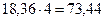Для обчислення третьої властивості дисперсії має місце така формула: , або 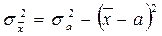. Обчислимо дисперсію відносно числа а (значення варіанти, що має найбільшу частоту), а не відносно середньої арифметичної і отримаємо число, що є більшим за стандартну дисперсію.

;

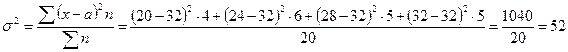
Дисперсію можна обчислити за більш простою формулою:

,

та способом відліку від умовного 0 (способом моментів), при умові, що маємо ряд з рівновеликими інтервалами,

.

Існує ще одна формула для визначення дисперсії способом моментів:

Побудувавши допоміжну таблицю, та обчисливши дисперсію за наведеними формулами, бачимо, що маємо однакові результати.

Таблиця. Дані для визначення дисперсії спрощеним способом та способом моментів

Урожайність, ц/га	Кількість господарств (частота)	Розрахункові дані
				–1	–4
Разом		Х		Х		Х

;

Дата добавления: 2015-08-10