Виды нагружения стержня

№1
Любая комбинация простых деформаций стержня называется …

			сложным сопротивлением
			напряженным состоянием
			деформированным состоянием
			тензором деформации

Решение:
Элементы конструкций при действии системы внешних сил могут испытывать одновременно несколько простых деформаций, например, растяжение и чистый изгиб, кручение и изгиб и т.д.
Случай, когда в стержне возникают различные комбинации простых деформаций, называется сложным сопротивлением.

№2

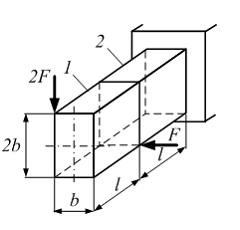
На стержень действуют внешние силы F и 2 F. Сечение прямоугольное с размерами b и 2 b. Участки стержня испытывают:
а) 1 – кручение, 2 – косой изгиб;
б) 1 – плоский поперечный изгиб, 2 – кручение и плоский поперечный изгиб;
в) 1 – кручение и плоский поперечный изгиб, 2 – косой изгиб;
г) 1 – кручение и плоский поперечный изгиб, 2 – кручение и косой изгиб.

			в
			а
			б
			г

Решение:
Используя метод сечений несложно определить внутренние силовые факторы на каждом участке. В поперечном сечении первого участка возникают поперечная сила , изгибающий момент 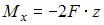, крутящий момент 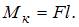Поэтому участок работает на кручение и плоский поперечный изгиб.

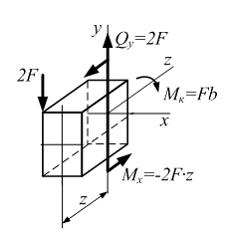
На втором участке в поперечном сечении стержня действуют поперечные силы 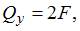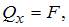изгибающие моменты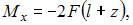 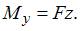Крутящий момент .

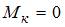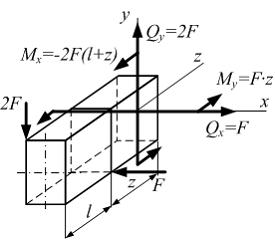
Второй участок испытывает косой изгиб.

№3
Оценку прочности материала при заданном напряженном состоянии в опасной точке стержня с круглым сечением проводят с использованием теорий прочности при:
а) внецентренном растяжении;
б) растяжении и плоском изгибе;
в) плоском поперечном изгибе;
г) кручении и изгибе.

			г
			а
			в
			б

Решение:
При кручении стержня с круглым сечением максимальные касательные напряжения возникают в точках, наиболее удаленных от оси вращения. Максимальные нормальные напряжения при изгибе действуют в точках, максимально удаленных от нейтральной линии. Нейтральная линия проходит через центр тяжести сечения и для круглого сечения расположена перпендикулярно плоскости действия изгибающего момента. Поэтому в опасной точке одновременно действуют максимальные нормальное и касательное напряжения. При оценке прочности материала в опасной точке совместное действие нормального и касательного напряжений заменяют, используя соответствующую теорию прочности, эквивалентным напряжением.

№4

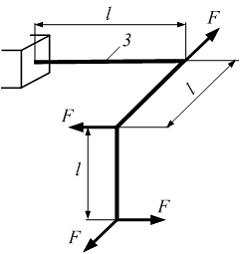
Схема нагружения стержня внешними силами представлена на рисунке. Длины участков одинаковы и равны l. Третий участок стержня испытывает деформации …

			кручение и чистый изгиб
			растяжение, кручение и чистый изгиб
			кручение и плоский поперечный изгиб
			кручение и растяжение

Решение:
Используя метод сечений, рассекаем третий участок произвольным сечением на две части. Рассмотрим равновесие правой части.

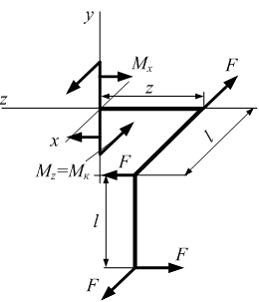
Из условий равновесия правой части следует, что в поперечном сечении отличны от нуля два внутренних силовых фактора:
изгибающий момент 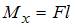и крутящий момент 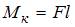. Следовательно, участок тртий испытывает деформации кручение и чистый изгиб.

№5
Напряженное состояние в опасных точках круглого поперечного сечения стержня считается плоским для случая:
а) плоский изгиб;
б) растяжение и плоский изгиб;
в) внецентренное растяжение;
г) растяжение с кручением.

			г
			а
			в
			б

Решение:
При совместных деформациях растяжение и кручение в поперечном сечении стержня возникает продольная сила и крутящий момент. Они вызывают, соответственно, нормальные и касательные напряжения. Нормальные напряжения при растяжении во всех точках поперечного сечения одинаковы. Максимальные касательные напряжения возникают в точках, наиболее удаленных от оси стержня. Следовательно, в опасных точках (точках, наиболее удаленных от оси стержня) возникают одновременно нормальное и касательное напряжения а напряженное состояние будет плоским.

№6
Напряженное состояние в опасных точках круглого поперечного сечения стержня считается линейным для случая:
а) изгиб с кручением;
б) растяжение с кручением;
в) внецентренное растяжение;
г) кручение и внецентренное сжатие.

			в
			а
			б
			г

Решение:
При внецентренном растяжении возникает продольная сила и изгибающий момент. Они вызывают только нормальные напряжения. Поэтому линейное напряженное состояние возникает в опасных точках при внецентренном растяжении. При других указанных вариантах наряду с нормальными напряжениями появляются касательные напряжения, обусловленные действием крутящего момента. Следовательно, напряженное состояние в опасных точках плоское.

№7

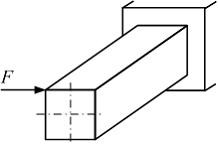
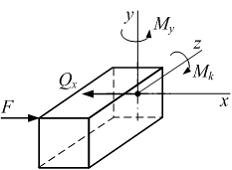
При данном варианте нагружения стержень прямоугольного поперечного сечения испытывает …

			кручение и плоский поперечный изгиб
			кручение и чистый изгиб
			плоский поперечный изгиб
			косой изгиб

Решение:
Рассечем стержень произвольным сечением на две части. Отбросим ту часть, где расположена заделка. Из условия равновесия оставшейся части видно, что в поперечном сечении отличны от нуля три внутренних силовых фактора: поперечная сила 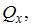изгибающий момент 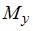и крутящий момент 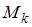. Следовательно, стержень испытывает деформации кручение и плоский поперечный изгиб.

№8

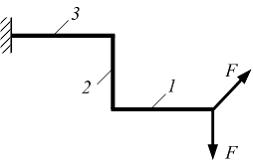
Схема нагружения стержня квадратного сечения внешними силами показана на рисунке (одна сила лежит в плоскости чертежа, вторая – перпендикулярно плоскости). Деформации (растяжение, кручение и плоский поперечный изгиб) одновременно возникают на участке (-ах) …

			2, 3

Решение:
Из анализа расчетной схемы следует, что только второй участок испытывает деформацию растяжение. Одновременно на этом участке в поперечном сечении стержня возникают крутящий момент, поперечные силы и изгибающие моменты.

№9
При выводе формул для определения напряжений в точке поперечного сечения стрежня при сложном сопротивлении используется …

			принцип независимости действия сил
			гипотеза об изотропности материала
			принцип неизменности начальных размеров
			гипотеза о сплошности материала

Решение:
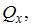
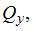
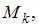
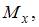
В общем случае нагружения стержня в поперечных сечениях могут возникнуть шесть внутренних силовых факторов – N, 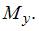При достаточно жестких стержнях совместное действие указанных усилий создает напряженное состояние в точке, которое можно получить суммированием напряженных состояний, вызванных каждым внутренним силовым фактором. Например, в точке поперечного сечения стержня можно определить нормальные напряжения от действия продольной силы 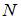, изгибающих моментов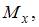 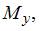а далее их просуммировать с учетом знаков. Принцип независимости действия сил применим во всех случаях, когда деформации малы и подчиняются закону Гука.

Дата добавления: 2015-08-10