Задание 8 (№ 27489)

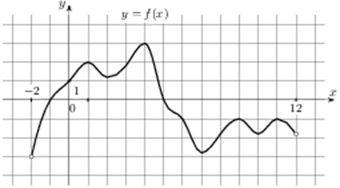
На рисунке изображен график функции 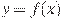, определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой 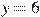или совпадает с ней.

y=6 – прямая параллельная оси OX

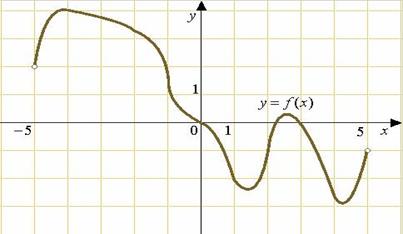Касательные к графику параллельны оси ОХ,когда они касаются точек экстремума (коэффициент k у прямой y=k*x+n должна быть равна нулю, и этот же коэффициент равен производной в этой точке, а при производной равной нулю точка-экстремум)

Посчитаем сколько точек экстремума у функции, это и есть наш ответ.

Таких точек 4, ответ: 4

30.(№ 27490)

На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремумов функции 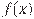.Суммой точек экстремума называется сумма абсцисс, координат точек экстремума

У нас 7 точек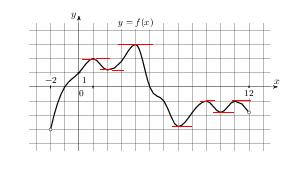

Складываем их абсциссы

1+2+4+7+9+10+11=44

Ответ:44

37. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

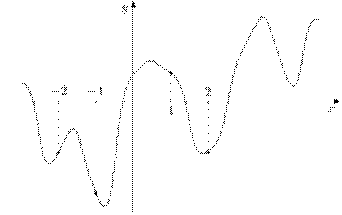
Нам известно, что если функция возрастает, то производная положительна, а если функция убывает, то производная отрицательна. Отсюда можем сделать вывод, что точки -1 и 1 не подходят. f’(x)=k=tg α,следовательно, необходимо сравнить угол наклона к оси ОХ в точке -2 и 2. Построив касательные, увидим, что в точке -2 угол больше, значит, в этой точке производная принимает наибольшее значение.

Ответ: -2

38. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

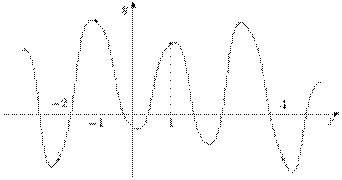
Нам известно, что если функция возрастает, то производная положительна, а если функция убывает, то производная отрицательна. Делаем вывод, что точки -2 и 1 не подходят.. f’(x)=k=tg α,следовательно, необходимо сравнить тангенсы углов наклона к оси ОХ в точке -1 и 4. Построив касательные, увидим, что в точке 4 угол меньше, значит, в этой точке производная принимает наименьшее значение

.

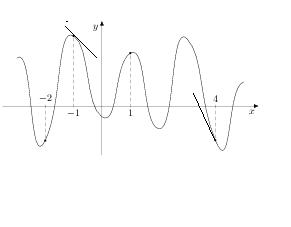
Ответ: 4

39. На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-2;4].

F(x) первообразная для f’(x), если F’(x) = f(x). По условию f(x)=0 => F’(x) =0. А это значит, что надо посмотреть количество экстремумов данной функции на заданном интервале.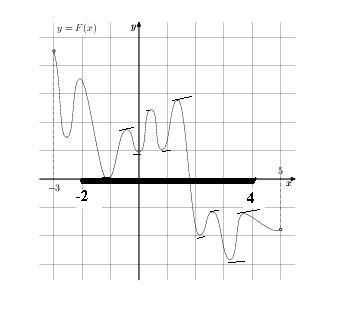

Ответ: 10

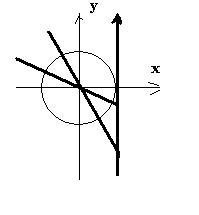
40. На рисунке изображён график функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)-F(2), где F(x) — одна из первообразных функции f(x).

Для данной задачи нам необходимо будет вычислить площадь фигура на рисунке на указанном интервале. Получается, что площадь трапеции будет равна: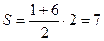

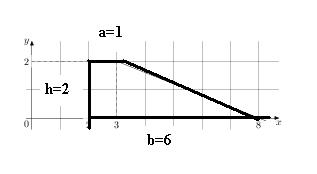
Ответ: 7

41. На рисунке изображён график некоторой функции y=f(x). Функция 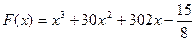— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

Для решения данной задачи необходимо знать, что определенный интеграл равен площади закрашенной фигуры.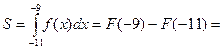

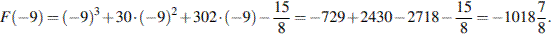
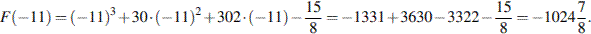
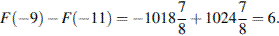
42. На ри­сун­ке изоб­ражён гра­фик не­ко­то­рой функ­ции 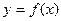. Функ­ция 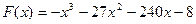— одна из пер­во­об­раз­ных функ­ции 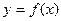. Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры.

Для решения данной задачи необходимо знать, что определенный интеграл равен площади закрашенной фигуры. 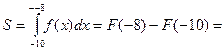4

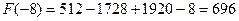
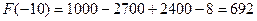
Ответ:4

Дата добавления: 2015-08-02