Задание 8 (№ 27503)

На рисунке изображены график функции 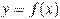и касательная к нему в точке с абсциссой 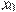. Найдите значение производной функции 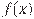в точке .

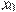Ход решения:

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс. Строим тре­уголь­ник с вер­ши­на­ми в точ­ках A (1; 2), B (1; −4), C(−2; −4). Угол на­кло­на ка­са­тель­ной к оси абс­цисс будет равен тангенсу угла ACB: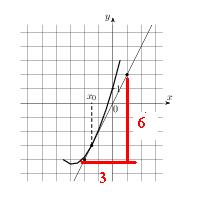

Y’(X0) = tg ACB= 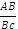= = 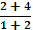2

Ответ: 2

19. На рисунке изображены график функции 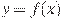и касательная к нему в точке с абсциссой 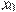. Найдите значение производной функции 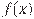в точке .

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс.   f’(x)=tgA=2:8=1:4=0,25  

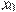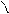
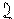
20. На рисунке изображены график функции 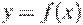и касательная к нему в точке с абсциссой 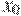. Найдите значение производной функции 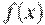в точке .

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс.   f’(x)=tgA=-tgB=-(8:4)=-2 знак минус возникает, так как угол А тупой  

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс.   f’(x)=tgA=-tgB=-(2:8)=-(1:4)=-0,25 знак минус возникает, так как угол А тупой  

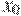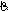
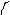
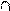
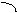
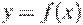21.На рисунке изображены график функции и касательная к нему в точке с абсциссой 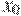. Найдите значение производной функции 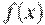в точке .

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной. По­сколь­ку ка­са­тель­ная па­рал­лель­на пря­мой или сов­па­да­ет с ней, она имеет уг­ло­вой ко­эф­фи­ци­ент рав­ный 2 и Оста­лось найти, при каких про­из­вод­ная при­ни­ма­ет зна­че­ние 2. Ис­ко­мая точка .

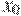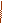
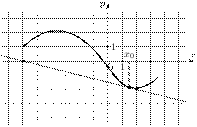
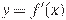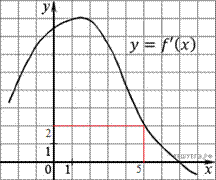
22.На рисунке изображен график — производной функции 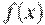. Найдите абсциссу точки, в которой касательная к графику параллельна прямой или совпадает с ней.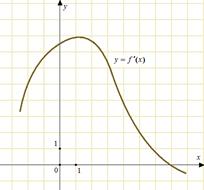

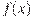23.На рисунке изображен график — производной функции . Найдите абсциссу точки, в которой касательная к графику 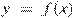параллельна оси абсцисс или совпадает с ней.

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной. По­сколь­ку ка­са­тель­ная па­рал­лель­на оси абс­цисс или сов­па­да­ет с ней, она имеет вид , и её уг­ло­вой ко­эф­фи­ци­ент равен 0. Сле­до­ва­тель­но, мы ищем точку, в ко­то­рой уг­ло­вой ко­эф­фи­ци­ент, равен нулю, а зна­чит, и про­из­вод­ная равна нулю. Про­из­вод­ная равна нулю в той точке, в ко­то­рой её гра­фик пе­ре­се­ка­ет ось абс­цисс. По­это­му ис­ко­мая точка .    

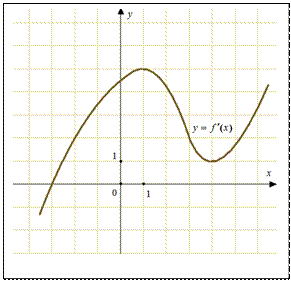
24.На рисунке изображен график функции 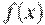, определенной на интервале 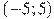. Найдите количество точек, в которых производная функции 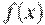равна 0.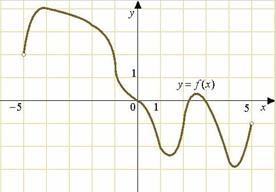

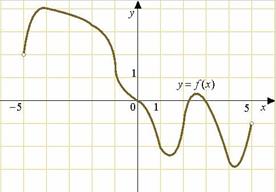
Производная равна нулю в точках экстремума. Ответ:425. Задание (№ 27485)

Прямая 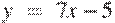параллельна касательной к графику функции 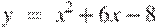. Найдите абсциссу точки касания.

Необходимо найти X₁ точки с координатами (X₁;Y₁)

Касательная к функции 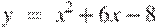параллельна 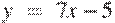, значит её формула

y=7x+n.

Производная квадратичной функции в точке X₁ равна коэффициэнту k при x в функции y=7х+n (то есть 7)

Берём производную и приравниваем её к семи.

2x+6=7

2х=1

x=0.5

X₁=0.5

Дата добавления: 2015-08-02