
Читайте также:
|
На рисунке изображён график функции 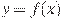 и двенадцать точек на оси абсцисс:
и двенадцать точек на оси абсцисс: 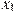 ,
, 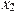 ,
, 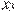 ,
, 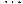 ,
,  . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 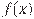 отрицательна?
отрицательна?

Если функция возрастает, то производная положительна, если функция убывает, то производная отрицательна. Поэтому производная данной функции отрицательна в точках x4;x5;x6;x7x8;x11;x12 => Ответ: в 7 точках.
11. Прототип задания 8 (№ 317541)
На рисунке изображён график 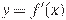 — производной функции — производной функции 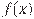 . На оси абсцисс отмечено восемь точек: . На оси абсцисс отмечено восемь точек: 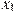 , , 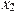 , , 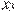 , , 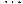 , , 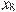 . Сколько из этих точек лежит на промежутках возрастания функции . Сколько из этих точек лежит на промежутках возрастания функции 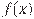 ? ?

| |
|
Чтобы определить промежуток возрастания функции по графику ее производной надо найти промежуток, на котором производная больше нуля То есть нам необходимо выделить все точки, которые лежат ВЫШЕ оси OX, а это x4; x5; x6 => Ответ: 3
Дата добавления: 2015-08-02; просмотров: 326 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Прототип задания 8 (№ 317539) | | | Прототип задания 8 (№ 317542) |