Данные для расчета элементов

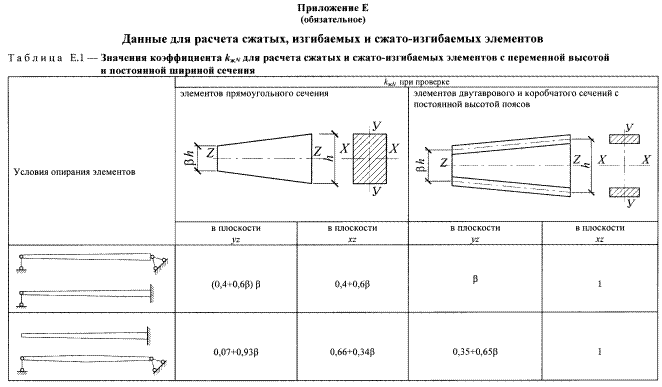
Т а б л и ц а Е.3 — Значения коэффициентов k и с для вычисления прогибов балок с учетом переменности сечения и деформаций сдвига

Поперечное сечение балки	Расчетная схема	k	с
Прямоугольное		β
То же		0,23+0,77β	16,4+7,6β
»		0,5α+(1–0,5α)β	[45-24α(1-β)+3β] * 1/(3-4α^2)
»		0,15+0,85β	15,4+3,8β
Двутавровое		0,4+0,6β	(45,3+6,9β)γ
Прямоугольное		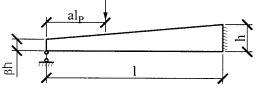0,23+0,77β+0,6α(1– β)	[8.2+2.4(1-β)α+3.8β] * 1/[(2+α)(1-α)]
То же		0,35+0,65β	5,4+2,6β
Примечание: γ — отношение площади поясов к площади стенки двутавровой балки (высота стенки принимается между центрами тяжести поясов).

ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ И ЦЕНТРАЛЬНО-СЖАТЫЕ ЭЛЕМЕНТЫ

Для прямоугольного сечения размером bh радиусы инерции можно подсчитывать по формулам:

r_х = 0,289h, r_у = 0,289в. Для круглого сечения диаметром dрадиусы инерции r_х = r_у = d/4.

Дата добавления: 2015-08-10