Читайте также:
|
Пусть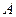 
и 
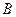– произвольные числовые множества: 
, 
.
Будем говорить, что на множестве 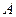задана функция 
, если для любого 
сопоставлено по определенному правилу или закону единственное значение 
.
Множество 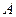называется областью определения функции и обозначается 
или 
: 
, 
.
Множество 
называется областью значений функции и обозначается 
или 
: 
, 
.
Если числу сопоставлено число , то есть , то 
называется аргументом или независимой переменной, а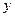 
– функцией или зависимой переменной.
Считается, что задана функция , если задана её область определения и для каждого значения 
сопоставлено значение функции 
, то есть задано правило или закон, по которому находится это значение. Правило установления соответствия 
может задаваться различными формами.
Отметим различие между обозначениями 
и . Символ – это обозначение функции, а – обозначение значения функции в точке . Для простоты изложения вместо термина «функция » будем использовать термин «функция », имея в виду функцию, определенную с помощью правила при .
Дата добавления: 2015-07-25; просмотров: 32 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Множество. Операции над множествами | | | Различные формы задания функции |