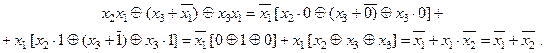Сформулювати теорему Шенона та на прикладі продемонструвати її застосування для спрощення логічних виразів.
Двійкові коди: зворотній, додатковий, Грея. Пояснити на прикладі особливості кожного та способи отримання з прямого коду. | Навести основні аксіоми та закони булевої алгебри. | На прикладі пояснити способи опису функціонування автомату Мілі за допомогою таблиць станів і виходів та графу переходів. | На прикладі пояснити способи опису функціонування автомату Мура за допомогою таблиці станів-виходів та графу переходів. | Перелічити етапи синтезу скінчених автоматів. Пояснити задачі абстрактного та структурного синтезу. Основні етапи синтезу скінченних автоматів | Навести скорочені таблиці станів асинхронних елементарних автоматів: RS-тригера і JK-тригера та пояснити відміни між ними. | Практична частина | Пояснення | Перетворити абстрактний автомат Мура, заданий графом, у еквівалентний автомат Мілі. Результат представити у вигляді графа та таблиці переходів. Пояснити виконані перетворення. |
Широке використання при перетворенні логічних функцій знаходять теорема Шенона та ряд тотожностей, які витікають з неї.
Теорема Шенона формулюється так: будь-яку функцію n зміних можна зобразити в формі:
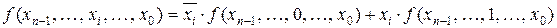 .
.
Теорема Шенона виявляється дуже корисною при виконанні перетворень логічних виразів, що містять операцію ВИКЛ. АБО.
Приклад. Виконати перетворення логічної функції:
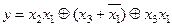 .
.
Розв’язання. Використовуючи теорему Шенона, виконаємо наступний ряд перетворень:
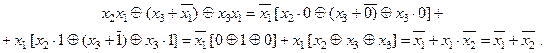
Дата добавления: 2015-07-21; просмотров: 67 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.007 сек.)

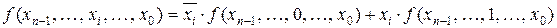 .
.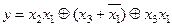 .
.