
Читайте также:
|
В булевій алгебрі логіки використовується ряд аксіом (тотожностей) та законів. Головні аксіоми та закони булевої алгебри:
Аксіоми (тотожності): 0 ∙ х = 0; 1 + х = 1; 0 + х = х; x ∙ х = х;
х + х = х;  ;
;  ;
; 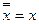 ;
;
Закони комутативності: х1 + х2 = х2 + х1; х1 ∙ х2 = х2 ∙ х1;
Закони асоціативності: х 1 + х 2 + х3 = х 1 + (х 2 + х 3) = (х 1 + х 2) + х 3 = (х 1 + х 3) + х 2;
х 1 ∙ х 2 ∙ х 3 = х 1 ∙ (х 2 ∙ х 3) = х 2 × (х 1 ∙ х 3) = х 3 × (х 1 ∙ х 2);
Закони дистрибутивності: х 1 ∙ (х 2 + х 3) = х 1 ∙ х 2 + х 1 ∙ х 3; х 1 + х 2 ∙ х 3 = (х 1 + х 2) ∙ (х 1 + х 3);
Закони інверсії (теорема де Моргана, принцип подвійності):
 ;
; 
 ;
;
Закони поглинання: х 1 + х 1 ∙ х 2 = х 1; х 1 ∙ (х 1 + х 2) = х 1.
Дата добавления: 2015-07-21; просмотров: 76 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Двійкові коди: зворотній, додатковий, Грея. Пояснити на прикладі особливості кожного та способи отримання з прямого коду. | | | Пояснити відмінність комбінаційних логічних схем від послідовнісних. Навести приклади. |