
Читайте также:
|
В "чистом" функциональном Лиспе нет ни циклических предложений ( for, progn и другие), ни тем более операторов передачи управления. Для программирования повторяющихся вычислений в нём используются лишь условные предложения и определения рекурсивных, или вызывающих самих себя, функций.
Например, рекурсивный вариант функции expt можно было бы определить так:
Функция expt вызывает себя до тех пор, пока используемый как счётчик аргумент n не уменьшится до единицы, т.е. всего лишь n-1 раз. После этого в качестве результата вызова функции expt возвращается значение this. При каждой передаче значения на предыдущий уровень результат умножается на this. Так this окажется перемноженным на себя n раз.
Рекурсивное определение функции expt короче, и лучше отражает суть функции, чем версии, основанные на for*.
Рассмотрим ещё одну функцию, просто определяемую через рекурсию, - факториал (факториал - это произведение данного числа на все целые положительные числа, меньшие данного. Например, факториал от 5, обозначаемый как 5!, есть 1*2*3*4*5=120. Факториалом нуля считается 1):
Итеративные и рекурсивные программы теоретически одинаковы по своим вычислительным возможностям, иными словами, множества вычислимых с их помощью функций совпадают (так называемые частично рекурсивные функции). Так что любое вычисление в принципе, можно запрограммировать любым из этих способов. Однако свойства итеративных и рекурсивных вариантов программ могут существенно отличаться. В связи с этим часто приходится решать, какой из способов программирования больше подходит для данной задачи. От сделанного выбора зависит простота и естественность программирования, а также его эффективность с точки зрения времени исполнения и использования памяти.
С помощью итеративного программирования, как правило, более длинного и трудного в осуществлении, результат может вычисляться значительно проще и быстрее. Это происходит по двум причинам, во-первых, потому, что вычислительные машины в общем ориентированы на пошаговые вычисления, и, во-вторых, потому, что трансляторы не всегда в состоянии преобразовать рекурсивное определение в итеративное и используют при вычислениях стек, несмотря на то что он не всегда нужен.
Рекурсивное программирование в общем более короткое и содержательное. Особенно полезно использовать рекурсию в тех случаях, когда решаемая задача или обрабатываемые данные по сути своей рекурсивны. Например, математическое определение факториала рекурсивно и его реализация через рекурсивную функцию совершенно естественна:
| n! = 1 | , если n=0 |
| n! = n*(n-1)! | , если n>0 |
Рекурсивное решение хорошо подходит для работы со списками, так как списки могут рекурсивно содержать подсписки. Рекурсивными функциями можно с успехом пользоваться при работе с другими динамическими структурами, которые заранее не полностью известны. Рекурсивные процедуры занимают важное место почти во всех программах, связанных с искусственным интеллектом.
Рекурсия (Lisp)
Рекурсия - один из основных приёмов программирования в декларативных языках, какими являются Пролог и Лисп. Предикат или функция называются рекурсивными, если они ссылаются на самих себя. При этом задача разбивается на части все меньшего и меньшего размера до тех пор, пока они не станут настолько малы, что их решение не будет сводиться к набору из одной или нескольких простейших операций.
Обычно рекурсивная программа состоит как минимум из двух частей:
Механизм рекурсии часто объясняют на вычислениях чисел Фибоначчи, первые 10 которых приведены в таблице:
| Числа Фибоначчи (первые 10 значений) | |||||||||||
| Номер числа Фибоначчи | |||||||||||
| Значение числа Фибоначчи |
Здесь каждое следующее число представляет собой сумму двух предыдущих чисел.
Эти числа могут быть определены следующим соотношением:
fib(0) = 1
fib(1) = 1
fib(n) = fib(n-1) + fib(n-2)
На рисунке представлена схема вычисления числа Фибоначчи с помощью рекурсии.
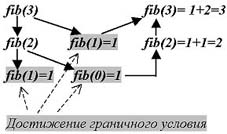
На Лиспе программа, реализующая эту функцию, будет выглядеть так:
(defun fib(n)
(if (< n 2) 1;граничное условие
(+ (fib (- n 1)) (fib (- n 2)))));рекурсивное условие
>(fib 10)
Дата добавления: 2015-07-21; просмотров: 68 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Циклические вычисления: предложения FOR, FOR*, WHILE и DO-WHILE | | | READ-LINE читает и возвращает выражение |