Законы Ома и Кирхгофа в комплексной форме. Параллельное соединение R,L,C элементов

Рассмотрим электрическую цепь на рисунке 15.

Рисунок 15 – Параллельное соединение -элементов

Запишем первое правило Кирхгофа для этой цепи

,

где ток в сопротивлении (ток совпадает по фазе с напряжением); ток индуктивности (ток отстаёт от напряжения на угол ); – ток в ёмкости (ток опережает напряжение на угол ).

Формула для определения комплексной проводимости запишется , где – активная, – реактивная проводимости.

Запишем закон Ома в комплексной форме ,

где или , где – модуль комплексного числа, а 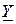– полная проводимость цепи равная , а – сдвиг фаз в цепи.

Построим векторные диаграммы. Рассмотрим электрическую цепь, у которой проводимость имеет индуктивный характер, т. е. 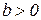и (рисунок 16).

Рисунок 16 – Векторная диаграмма

Для случая когда реактивная проводимость имеет емкостной характер, т. е. , , векторная диаграмма представлена на рисунке 17.

Рисунок 17 – Векторная диаграмма

Нарисуем треугольник проводимостей для двух случаев. Если полная проводимость цепи 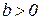и полная проводимость цепи (рисунок 18):

Рисунок 18 – Треугольники проводимостей

Дата добавления: 2015-07-20