Ілюстрація у вигляді короткого запису

Ілюстрація у вигляді короткого запису (схематичного, табличного) чи рисунка фіксує у зручній для сприймання формі величини (дані і шукані), допомагає розкрити залежності між ними.

Під час ознайомлення із задачею нового виду, використовують яку-небудь одну ілюстрацію, але у деяких випадках буває корисно проілюструвати задачу як предметно, так і схематично. У свою чергу, схематичне зображення якого-небудь виду задач не обов’язково повинне мати єдину форму. При нагоді варто показувати дітям різні форми короткого запису однієї і тієї ж задачі чи задач одного виду.

У знаходженні неявної залежності між запитанням задачі і даними полягає інтерес дітей до процесу розв’язування задач, а це сприяє розвитку їхнього мислення. Тому недоцільно намагатися якомога частіше розкривати зв’язки у задачах за допомогою короткого запису чи застосування іншої наочності.

Розв’язувати задачі з використанням короткого запису слід у таких випадках [11]:

- При початковому розв’язуванні простих задач, коли цей процес є переходом від операцій над множинами предметів до арифметичних дій над натуральними числами;

- При розв’язуванні простих і складених задач з метою формування в учнів уявлення про структуру задачі;

- При використанні задач для формування математичних понять, ознайом-лення учнів з елементами арифметичної теорії чи залежностями між величи-нами;

- При початковому ознайомленні учнів із задачею нового виду (і то не зав-жди), а також тоді, коли багато учнів не можуть самостійно розв’язати задачу.

Учнів слід поступово привчати до короткого запису задачі. У другому класі учні наслідують зразок учителя. Як самостійну роботу на уроці слід практикувати запис даних у задану схему. Вдома другокласники розв’язують задачу без короткого її запису. У 3 – 4 класах учитель дає зразки чи опорні схеми коротких записів, а й ознайомлює дітей з деякими рекомендаціями щодо їх виконання.

Учні повинні знати, що в короткому записі треба використовувати слова, які визначають дію або залежність між даними і шуканою величинами. Зв’язані між собою дані слід записувати в одному рядку; число, яке є сумою кількох даних, записувати справа або зліва від них і відокремлювати рискою; запитання задачі позначати знаком запитання або буквою х. Проміжні дані також позначати цим знаком. У табличній формі два значення однієї і тієї ж величини треба записувати одне під одним.

Короткий запис задачі – це засіб навчання, а не складова частина програми з математики. Тому при проведенні контрольної роботи не можна вимагати від учнів, щоб вони робили короткий запис задачі.

Зупинимося більш детально на особливостях ілюстративно-пояснювальної технології розв’язування деяких текстових задач з використанням короткого запису у різних видах.

Використання короткого запису у вигляді таблиці

Задача 1 [16, с. 112, № 738].

Бензин був у п’яти каністрах, у кожній порівну. У перший автомобіль заправили 54 л бензину, а в другий 36 л. Скільки каністр бензину було заправлено у перший автомобіль і скільки у другий?

	Місткість каністр	Кількість каністр	Кількість бензину
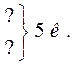
Перший автомобіль Другий автомобіль	Однакова		54 л 36 л

Як видно із таблиці, у задачі розглядаються три взаємопов’язаних величини: місткість каністр, кількість каністр та кількість бензину. Щоб визначити одну з цих величин, треба знати дві інших. Для того, щоб знайти кількість каністр з бензином, якими заправили кожний з автомобілів, треба бензин, що міститься в цих каністрах, поділити на місткість каністр. Місткість каністр однакова, кількість каністр відома, кількість бензину в цих каністрах можна знайти дією додавання. Після цього можна знайти місткість кожної каністри.

План розв’язування

1) Знаходимо кількість бензину, яким заправили обидва автомобілі;

2) Обчислюємо місткість кожної каністри;

3) Підраховуємо, скільки каністр бензину заправили у перший автомобіль;

4) Підраховуємо, скільки каністр бензину заправили у другий автомобіль.

Задача 2. [16, c. 123, № 825,].

Один вертоліт пролетів 480 км, а другий 800 км. Перший вертоліт був у польоті на 2 години менше. Скільки годин був у польоті кожний вертоліт, якщо їх швидкість однакова?

	Швидкість	Час	Відстань
Перший вертоліт Другий вертоліт	Однакова	?, на 2 год менше ?	480 км 800 км

У цій задачі розглядаються три взаємопов’язаних величини: швидкість, час, відстань. Щоб знайти час польоту, треба відстань поділити на швидкість. Швидкість невідома, її треба знайти. Звертаємо увагу на те, що вертольоти були у польоті різний час, тому і відстані, які вони пролетіли, різні. Різницю у відстані визначає різниця у часі, оскільки швидкість у них була однакова. Якщо перший вертоліт був у польоті на дві години менше, ніж другий, то другий був у польоті на дві години більше, ніж перший. Знайшовши, яку відстань подолав другий вертоліт за ці дві години, зможемо знайти і швидкість кожного з вертольотів.

План розв’язування

1) Обчислюємо, скільки кілометрів пролетів другий літак за дві години;

2) Вираховуємо швидкість кожного вертольота;

3) Знаходимо час польоту першого вертольота;

4) Знаходимо час польоту другого вертольота.

Схематична ілюстрація умови задачі

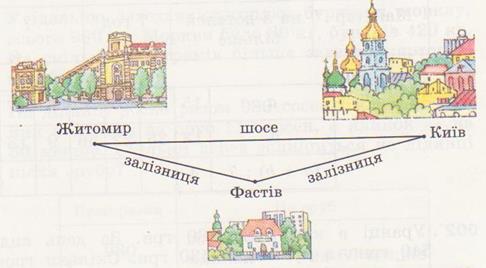
В підручниках з математики для початкової школи є досить багато задач, сюжет яких можна наглядно відобразити, використовуючи схематичні ма-люнки. Зокрема, це задачі на рух, в тому числі, на зустрічний рух і на рух в протилежних напрямках. В таких схемах відстань між пунктами руху позна-чається відрізками, напрям руху – стрілками. Деякі схеми до найпростіших задач на рух подаються у підручниках. Наприклад, така задача [15, с. 91, № 596]:

Відстань від Києва до Житомира залізницею (через Фастів) 150км, а по шосе на 20км менша. Турист з Києва до Житомира їхав залізницею, а назад повертався автобусом. Скільки всього кілометрів проїхав турист?

Більш абстрактною є схема іншої задачі [15, с. 24, № 161]:

Відстань між двома містами 250 км. Із цих міст назустріч один одному одночасно виїхали два автобуси. Яка відстань була між автобусами, коли перший із них проїхав 127 км, а другий 93 км?

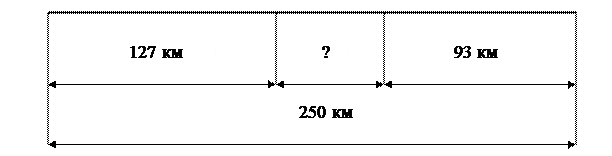
При роботі із цією задачею можна притримуватись такої послідовності.

− Покажіть місто, з якого виїхав перший автомобіль. Покажіть місто, з якого виїхав другий автомобіль. Яка відстань між цими містами? Покажіть її на схемі.

− Покажіть відстань, яку проїхав перший автомобіль. Скільки це становить кілометрів?

− Покажіть на схемі відстань, яку проїхав другий автомобіль. Скільки це становить кілометрів?

− Покажіть на схемі відстань, яка була між ними після того, коли кожний із них проїхав вказану кількість кілометрів. Як знайти скільки кілометрів становить ця відстань?

При вивченні прийомів розв’язування задач на зустрічний рух можна користуватися схематичним зображенням ситуації, що описується в наступній задачі:

Задача (На знаходження відстані, що була між об’єктами на початку руху).

З двох міст одночасно назустріч один одному виїхали два автобуси і зустрілися через 3 години. Перший автобус рухався із швидкістю 60 км/год, а другий − 62 км/год. Знайти відстань між містами.

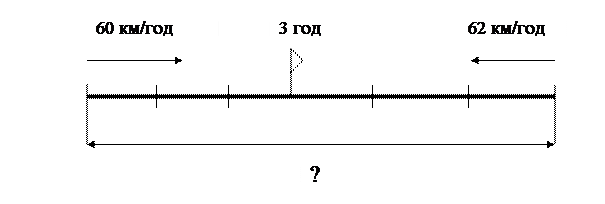
Перший спосіб

− З яких частин складається відстань між містами?

− Покажіть на схемі відстань, що проїхав перший автобус. Які величини треба знати, що знайти відстань? Чи можемо знайти скільки кілометрів проїхав до зустрічі перший автобус? Як?

− Покажіть на схемі відстань, яку проїхав до зустрічі другий автобус. Чи можемо знайти. Скільки кілометрів до зустрічі проїхав другий автобус? Як?

План розв’язування

1) Скільки кілометрів до зустрічі проїхав перший автобус?

2) Скільки кілометрів до зустрічі проїхав другий автобус?

3) Скільки кілометрів становить відстань між містами?

Другий спосіб

− Покажіть місцезнаходження першого і другого автобусів через годину після початку руху. Як можна охарактеризувати ситуацію щодо їх місцезнаходження? (автобуси зблизились на відстань, що дорівнює сумі відстаней, пройдених кожним з автобусів за годину).

− Покажіть місцезнаходження першого і другого автобусів через дві години після початку руху. На скільки тепер автобуси зблизились?

− Що можна сказати про розташування автобусів один відносно одного через три години після початку руху? Чому дорівнює відстань, на яку автобуси зблизились в момент зустрічі? Як обчислити цю відстань?

План розв’язування

1) На скільки кілометрів зближувались автобуси щогодини?

2) Яка відстань між містами?

Подібними схемами можна ілюструвати задачі на зустрічний рух, в яких знаходиться час до зустрічі та швидкість одного з рухомих об’єктів, врахову-ючи той факт, що вони є оберненими задачами до задачі на знаходження відстані між пунктами при одночасному зустрічному рухові.

Графічна ілюстрація умови задачі

Графічна ілюстрація задач базується на тому, що числові значення величин, про які йде мова у задачі, схематично відображаються у вигляді відрізків. Між цими відрізками існує таке ж відношення, як і між величинами, про які йде мова у задачі. При первинному ознайомленні із таким способом зображення кількості чи певних величин малюнок дається з дотриманням масштабу, як у випадку такої задачі [15, с. 12, №59]:

Склади задачу, розв’яжи її окремими діями.

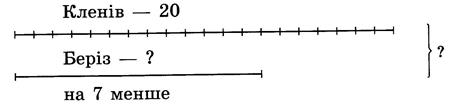
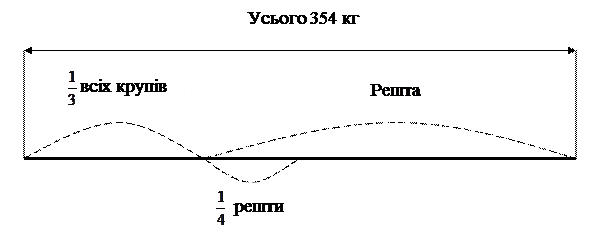
Проте у більшості випадків графічна ілюстрація має дещо схематичний характер [16, с. 31, № 209]:

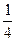У магазині було 354 кг крупів. Рис становив всіх крупів, а пшоно – решти крупів. Скільки пшона було в магазині?

Розглянемо методику розв’язування деяких типів задач з використанням такої графічної ілюстрації.

Задача 1 [ 16, с. 45, № 287]

Корова дала за два удої 25 л молока. Вранці вона дала на 3 л молока більше, ніж увечері. Скільки літрів молока дала корова вранці і скільки увечері?

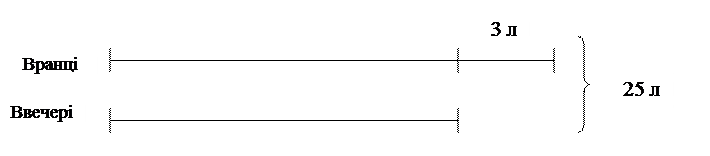
Пошук шляхів розв’язання

Уявно урівняємо удій молока вранці і увечері. Це можна зробити двома способами:

а) Зменшити вранішній удій на 3 л, тоді і денний удій зменшується на 3л. Тоді схематичне зображення умови задачі буде мати вигляд

	Вранці
				(25 – 3) л
	Ввечері

І уже видно спосіб розв’язування задачі:

1) Знаходимо, яким був би денний удій молока, якщо б вранці надоїли стільки молока, скільки увечері:

25 – 3 = 22 (л).

2) Обчислюємо, скільки молока надоїли від корови увечері:

22: 2 = 11 (л).

3) Вираховуємо, скільки молока надоїли від корови вранці:

11 + 3 = 14 (л).

3 л  

б) Збільшимо вечірній надій на 3 л, тоді і весь денний надій збільшується на 3 л. У цьому випадку схематичне зображення умови задачі матиме вигляд

	Вранці
	Ввечері

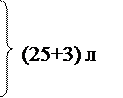Ця схема дає другий спосіб розв’язування задачі:

1) Знаходимо, яким був би денний удій молока, якщо б увечері надоїли молока стільки, скільки уранці: 25 + 3 = 28 (л).

2) Обчислюємо, скільки молока надоїли від корови вранці: 28: 2 = 14 (л).

3) Підраховуємо, скільки молока надоїли від корови увечері: 14 – 3 = 11 (л).

Розв’язування задачі двома різними способами дало одну і ту ж відповідь: вранці від корови надоїли 14 л молока, а увечері – 11 л. Можна зробити і ще одну перевірку. 14 + 11 = 25 (л) молока надоїли за день, як і в умові задачі.

Використовуючи подібну графічну ілюстрацію, можемо розв’язати таку задачу [ 16, с. 81, № 511]:

Задача 2. Периметр прямокутника 24 дм. Його ширина на 4 дм менша від довжини. Знайти площу прямокутника.

Розв’язання

1)

4 дм

Довжина

Ширина

Скільки дециметрів становить сума довжини і ширини прямокутника? 24: 2 = 12 (дм).

	12 дм

2) Скільки дециметрів становила б сума довжини і ширини прямокутника, якщо б ширина була такою, як довжина? 12 + 4 = 16 (дм).

3) Яка довжина прямокутника? 16: 2 = 8 (дм).

4) Яка ширина прямокутника? 8 – 4 = 4 (дм). Перевірка: (8 + 4) ∙ 2 = 24 (дм) – периметр прямокутника, як і в умові.

5) Скільки квадратних дециметрів становить площа прямокутника? 8 ∙ 4 = 32 (дм²).

Відповідь: Площа прямокутника 32 дм².

Графічна ілюстрація значно полегшує відшукання алгоритму розв’язання задачі і у випадку, коли у задачі між величинами чи числами задане відношення «більше у …».

Задача 3. [22, с. 80, № 58]:

На автобазі було на 46 вантажних автомобілів менше, ніж автобусів. Скільки вантажних автомобілів було на автобазі, якщо їх було у 3 рази менше, ніж автобусів?

Пошук шляхів розв’язання

Вантажні автомобілі

Автобуси

Позначимо кількість автомобілів відрізком. Оскільки автобусів було у 3 рази більше, ніж автомобілів, то відрізок, що позначає кількість автобусів, складається з трьох частин, кожна з яких дорівнює кількості автомобілів. Автомобілів на 46 більше ніж автобусів. Із схеми видно, що число 46 утворюють дві частина, кожна з яких така ж як і кількість автомобілів. Отже автобусів на автобазі було 46: 2 = 23.

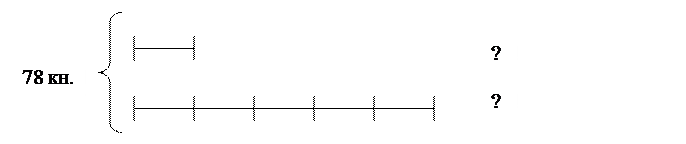
Задача 4. [22, с. 87, № 101]:

На двох полицях було 78 книжок. На одній полиці книжок було у 5 разів більше, ніж на другій. Скільки книжок на кожній полиці?

Розв’язання

1) Скільки рівних частин становлять книги на двох полицях? 1+ 5 = 6 (ч.)

2) Скільки книг було на першій полиці? 78: 6 = 13 (к.)

3) Скільки книг було на другій полиці? 12 ∙ 5 = 65 (к.).

Перевірка: 13 + 65 = 78 (к.) було на двох полицях, як і в умові задачі.

Відповідь: на першій полиці було 13 книг, на другій – 65 книг.

Пошук шляхів розв’язання задачі з використанням блок-схеми

?

?

1)

2)

Формуванню умінь учнів розв’язувати текстові задачі сприяє також використання в процесі пошуку шляхів розв’язання задачі певної блок-схеми алгоритму розв’язання задачі. Розглянемо методику роботи з такою блок-схемою на прикладі задачі з підручника [15, с. 52, №335]: У 5 ящиків розклали порівну 30 кг вишень. Скільки потрібно таких ящиків, щоб розкласти 54 кг вишень?

Це новий для учнів вид задач. Після ознайомлення учнів із змістом задачі, пошук шляхів розв’язання вчитель проводить з використанням поданої у підручнику блок-схеми. Бесіду можна провести таким чином: – На скільки дій дана задача?

– Над якими числами виконується перша дія? Що означає число 30? Що показує число 5? Яку величину можна знайти, маючи масу вишень і кількість ящиків, в які розклали ці вишні? Якою дією?

– Над якими числами виконується друга дія? Що показує число 54? Отже ми маємо масу вишень і масу вишень в кожному ящику, що можемо знайти, маючи ці дані? Якою дією?

Так складена блок-схема алгоритму розв’язання задачі передбачає синте-тичний спосіб пошуку шляхів розв’язання задачі. Подібну блок-схему можна використати і при аналітичному способі пошуку шляхів розв’язання. Наведемо зразок таких міркувань на прикладі наступної задачі [17, с. 111]:

За 6 днів садівник обрізав 240 дерев. Скільки дерев обріже садівник за той самий час, якщо щодня обрізатиме на 10 дерев більше, ніж обрізав кожного попереднього дня?

Пошук шляхів розв’язання

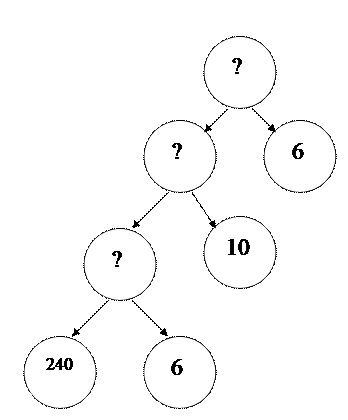
– Розглянемо схему, яка буде для нас підказкою для відшукання способу розв’язування цієї задачі. Вона починається із знака запитання. Він означає запитання задачі. Нагадаємо, що питається в задачі.

– Який час буде садівник обрізати дерева? (6 днів). Що ми маємо ще знати, щоб дізнатися скільки всього дерев обріже садівник? (скільки дерев він обрізатиме щодня). Чи знаємо цю кількість дерев? Отже кількість дерев, яку він має обрізати щодня, невідома. Чи сказано щось про неї в умові задачі? (вона на 10 дерев більша за ту, яку садівник обрізав раніше). Чи знаємо, скільки дерев щодня обрізав садівник? Чи можемо знайти? Як?

– А тепер, дивлячись на схему, складаємо план розв’язування задачі. 1) По скільки дерев обрізав садівник щодня?

2) По скільки дерев щодня має обрізати садівник?

3) Скільки дерев обріже садівник за 6 днів?

Показавши учням послідовність міркувань з опорою на схему, вчитель може в процесі пошуку шляхів розв’язання тієї чи іншої задачі вчити учнів складати подібні схеми самостійно [11, с. 134 - 136]. У цьому випадку аналіз задачі і план її розв’язування буде мати компактне графічне зображення.

Відомий педагог Логачевська С.П. у своїх посібниках [18 - 21] розробила з використанням пояснювально-ілюстративного методу технологію навчання учнів способів розв’язування кожного виду задач, які вивчаються у початковій школі. Автор починає з повного розбору задачі, включаючи відповідну ілюстрацію сюжету задачі: предметну чи схематичну. Дається розв’язання задачі, звертається увага на головний факт, який потрібно запам’ятати, щоб успішно розв’язувати подібні задачі. Далі наводиться приклади задач даного виду, які супроводжуються певними міркуваннями-підказками. З кожним разом цих підказок стає все менше і менше і, нарешті, потрібно розв’язати задачу уже без підказок. Та на цьому не завершується процес навчання розв’язувати задачі цього виду. Учням пропонуються різноманітні творчі завдання, пов’язані із складанням задач. Продемонструємо цю технологію на прикладі навчання учнів розв’язування задач на збільшення числа на кілька одиниць і у кілька разів [20, c.50 - 53].

Вразовуючи все вище сказане, можемо підсумувати наступним чином:

1. Одним із найважливіших моментів в процесі навчання молодших школярів розв’язувати текстові задачі є широке і вміле використання учителем-класоводом ілюстративно-пояснювального методу у всіх його багатогранних проявах.

2. Ілюстративно-пояснювальний метод реалізується використанням в процесі ознайомлення з текстом задачі та в процесі знаходження шляхів розв’язування цієї задачі таких моментів: – предметна ілюстрація умови задачі; – короткий запис задачі у різних формах, в тому числі, і у вигляді таблиці; – схематична ілюстрація умови задачі; – графічна ілюстрація умови задачі; – використання блок-схем алгоритму розв’язування задачі; – використання різних підказок на шляху відшукання способу розв’язування задачі.

3. Успішне використання ілюстративно-пояснювального методу в про-цесі навчання учнів розв’язувати текстові задачі ґрунтується на вда-лому підборі до конкретної задачі того чи іншого прийому або вміло-му поєднанні кількох складових цього методу.

Дата добавления: 2015-07-20