Читайте также:
|
Запорожская государственная инженерная академия
А.Я. Жук, Май Фыок Туан
ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ И ТЕХНИКА ЭКСПЕРИМЕНТА
Раздел «Математическая обработка эксперимента»
Учебно-методическое пособие для студентов
специальности 7.090218 «Металлургическое оборудование»
Запорожье
Министерство образования и науки Украины
Запорожская государственная инженерная академия
Утверждено к печати
ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ И ТЕХНИКА ЭКСПЕРИМЕНТА
Раздел «Математическая обработка эксперимента»
Учебно-методическое пособие для студентов
специальности 7.090218 «Металлургическое оборудование»
Запорожье
1. ОБЩИЕ ПОЛОЖЕНИЯ ТЕОРИИ ОШИБОК
Конечным продуктом любого эксперимента в большинстве случаев являются данные, записанные в той или иной форме. В простых экспериментах могут быть весьма элементарные данные и не содержать каких-либо ошибок. Примером может служить счет числа простоев механизма из-за поломки или износа деталей. С другой стороны, если производятся измерения каких-либо параметров с помощью измерительных приборов, инструментов и т.д., данные эксперимента, какой бы он ни был простой, будут содержать ошибки. Примером здесь может служить измерение частоты вращения электродвигателя, длины стержня, величины перемещения и др. Это связано с тем, что никакое измерение не может быть выполнено достаточно точно. Его результат всегда содержит ошибку. Поэтому в задачу измерений входит не только нахождение самой величины, и оценка допущенной при измерении погрешности.
При измерении физических величин существует три основных источника ошибок:
- прибор или датчик неправильно отражают измеряемую величину;
- неспособность индикатора или какой-либо части прибора правильно отражать реакцию воспринимающего элемента;
- неспособность наблюдателя правильно регистрировать показания прибора.
Эти три источника погрешности приводят к двум основным классам ошибок: случайным и систематическим.
Систематические ошибки связаны с ограниченной точностью измерения прибора, неправильным выбором метода измерения, неправильной установкой прибора и т.п.
Случайные ошибки носят случайный характер. В основе теории этих ошибок лежат два предположения, подтверждаемых опытом:
- при большом числе измерений случайные ошибки одинаковой величины, но разного знака, встречаются одинаково часто;
- большие по абсолютной величине ошибки встречаются реже, чем малые.
На основе этих предположений Гауссом выведен закон нормального распределения, на котором и базируется теория случайных ошибок.
2 оценка случайных ошибок
Для оценки величины случайной ошибки измерения существует ряд способов. Однако наиболее распространена оценка с помощью средней квадратичной ошибки.
Средняя квадратичная ошибка отдельного измерения определяется по формуле:
(2.1)
Здесь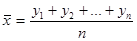 
- среднее арифметическое величин у1, у2, …, уn.
Средняя квадратичная погрешность результата серии измерений определяется по формуле:
(2.2)
Однако бывают случаи, когда одно (или несколько) измерений резко отличаются по своему значению, то следует проверить, не являются ли они промахом.
3 выявление и исключение промахов
Промахи относятся к числу случайных ошибок, но явно отличающихся своей величиной от величин остальной серии измерений. Если серия из небольшого числа измерений содержит грубую погрешность - промах, то наличие его может сильно исказить как среднее значение измеряемой величины, так и границы доверительного интервала. Поэтому из окончательного результата необходимо исключить этот промах.
Для исключения промахов пользуются формулами:
(3.1)
где 
(3.2)
y(n) – наибольшее значение измерений в серии n измерений;
у(1) – наименьшее значение в этой же серии.
В таблице 3.1. приведены значения V max - максимально возможное значение V(n), возникающие вследствие статического разброса и соответствующие заданной надежности α (кроме того, коэффициент α носит еще название доверительной вероятности). Значение V max возрастает с увеличением надежности α и числа измерений n. Это означает, что данное значение y(n) несовместимо с исходным предположением о законе нормального распределения и его можно рассматривать как промах. Это измерение следует исключить и определить новое значение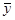 
. Если же величина V(n), соответствующая значению y(n) меньше V max для этого же числа измерерний при заданной надежности α, то это резко выделяющиеся измерения y(n) является следствием систематического разброса, и нет оснований считать его промахом.
Таблица 3.1 Значение V max при разных значениях числа измерений n и для разных надежностей α.
| n | α=0,90 | α=0,95 | α=0,99 | n | α=0,90 | α=0,95 | α=0,99 |
| 1,41 | 1,41 | 1,41 | 2,04 | 2,17 | 2,37 | ||
| 1,64 | 1,69 | 1,72 | 2,10 | 2,24 | 2,46 | ||
| 1,79 | 1,81 | 1,96 | 2,15 | 2,29 | 2,54 | ||
| 1,89 | 2,00 | 2,13 | 2,19 | 2,34 | 2,61 | ||
| 1,97 | 20,9 | 2,26 | 2,23 | 2,39 | 2,66 |
Рассмотрим на примере технологию исключения промахов. Для этого воспользуемся исходными данными, приведенными в таблице 3.2.
Таблица 3.2 Исходные данные для примера.
| n | Точка 1 | Точка 2 | Точка 3 | Точка 4 | Точка 5 | Точка 6 | Точка 7 | |||||||
| х | у | х | у | х | у | х | у | х | у | х | у | х | у | |
| 20,1 24,9 22,2 16,2 18,7 | 33,8 39,5 31,6 28,8 37,1 | 44,9 48,9 46,6 42,7 39,1 | 53,8 59,0 56,9 49,4 44,0 | 61,6 67,6 64,3 58,7 56,0 | 68,3 73,2 70,8 65,4 62,5 | |||||||||
| Среднее значение у | 20,42 | 34,16 | 44,44 | 52,62 | 61,64 | 68,04 |
Из чисто визуального рассмотрения вызывает сомнение число «44,0» для точки 5.
Перед тем, как определить V для этой величины, сначала вычислим значение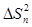 
по (3.2).
Среднее значение 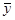для точки 5 составит:
Отклонение подозреваемой величины:
52,62-44,0=8,62
Тогда
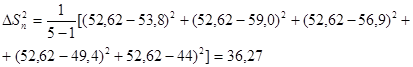
и
Из таблицы 3.1 для n=5 и α=0,95 V max =1,81
Т.о. V< V max и, следовательно, нет основания считать величину у=44,0 промахом.
4 определение вида функциональной зависимости и ее математическое описание
Этот вопрос является одним из основных при обработке результатов исследований, методика обработки которых, помимо вида проведения эксперимента, зависит от вида зависимости переменных. Существуют четыре основных вида.
1. Зависимость между двумя неслучайными переменными (схема А).
2. Зависимость случайной переменной от неслучайной переменной (схема Б).
3. Зависимость между двумя случайными переменными (схема С1 и С2).
При схеме А переменная у вполне определенно задается значением переменной х, т.е. значение у зависит только от соответствующих значений х и полностью ими определяются. Это чисто функциональная зависимость и не содержит никаких элементов случайности в определении величины х и у. Поэтому при проведении анализа нет необходимости использовать методы вероятностно-статистической теории. При такой схеме ограничиваются лишь построением графика зависимости переменных и анализом их связи.
При схеме Б измерение переменной у связано с некоторыми погрешностями измерения, а переменная х измеряется без ошибок или же они незначительны в сравнении с погрешностями зависимой переменной у. При обработке результатов в этом случае применяется регрессионный анализ, неотъемлемой частью которого является метод наименьших квадратов. В соответствии с этим методом квадрат разности между левой и правой частями функций должен быть минимальным.
Обработка включает построение наилучшей прямой (кривой) на графике с помощью метода наименьших квадратов и, если возможно, определение доверительных интервалов, попадание в которые индивидуальных или средних значений у при каждом фиксированном значении х гарантировалось бы с заранее заданной вероятностью.
При схеме С1 исследуемые величины зависят от совокупности неконтролируемых факторов, так что являются случайными по своей физической сущности. В этом случае используется корреляционный анализ, при котором производится исследование степени тесноты связи между переменными, построение конкретной зависимости и определение ее точности различают степени связи: тесную и слабую или нулевую, при которой изменение одной переменной не вызывает изменение другой.
Теснота связи устанавливается путем определения коэффициента корреляции (при линейной корреляции) и корреляционного отношения (при криволинейной корреляции). Оба лежат в пределах 0…1. Чем ближе их значение к единице или равных единице будет иметь место определенная функциональная зависимость. Это дает основания применить регрессионный анализ с построением математической зависимости.
При схеме С2 исследуемые величины не случайны, однако могут быть измерены с некоторыми случайными ошибками измерения. При этой схеме, в зависимости от конкретного случая, для обработки результатов измерения может быть применен регрессионный или корреляционный анализ.
После выявления и исключения промахов, если они имеют место, по средним значениям для каждой точки строят график (рис. 4.1). Средние значения для примера приведены в таблице 3.2.
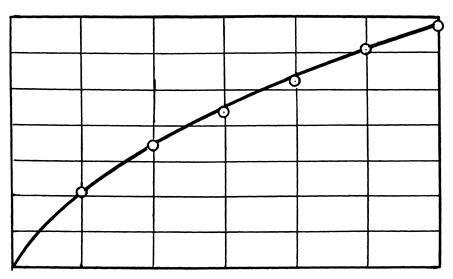
Рисунок 4.1 – График зависимости у=f(х), построенный по средним значениям у.
Построив график, приступаем к распознаванию вида функциональной зависимости. Для этого пользуются математической справочной литературой, где приводятся самые разнообразные графики и их математическое описание.
Предположим, что эта функциональная зависимость имеет вид:
у=ахк (4.1)
где а – постоянный коэффициент;
к – степень.
Если есть основания считать, что это так, то приступают к определению численных значений а и к. Если же нет, то определяют достоверность принятого вида функций методом выравнивания. Он заключается в предположении, что между у и х существует зависимость определенного вида. Для нашего случая (4.1) перевести в логарифмическую форму, т.е.
lg y=lg a+klg x (4.2)
или Y=A+kX (4.3)
Изучение выражения (4.3) показывает, что его графическое изображение имеет прямую линию, не проходящую через начало координат. Вычисляя для заданных значений х, у, соответствующие значениям Х, Y и изображая их графически, легко сразу увидеть, близка ли зависимость между Х и Y к линейной (ложатся ли соответствующие точки приблизительно на прямую линию) и, следовательно, подходит ли выбранная формула.
Для построения графика, пользуясь таблицей 3.2, найдем логарифм необходимых величин (таблица 4.1).
Таблица 4.1 Логарифмы необходимых величин
| Точка 1 | Точка 2 | Точка 3 | Точка 4 | Точка 5 | Точка 6 | Точка 7 | |
| х Х | 1,000 | 1,301 | 1,477 | 1,602 | 1,699 | 1,778 | |
| у Y | 20,42 1,310 | 34,16 1,533 | 44,44 1,648 | 52,62 1,721 | 61,64 1,790 | 68,04 1,833 |
По данным таблицы 4.1 строим график (рис. 4.2), приняв А=0 и к=1.
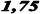
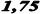
Рисунок 4.2 – График выравнивания.
Из графика (рис. 4.2) видно, что значение Y практически располагается на прямой линии, что дает основания считать правильным выбор вида функциональной зависимости.
5 определение параметров функциональной зависимости
Для этой цели используем регрессионный анализ на основе метода наименьших квадратов, в соответствии с которым можно записать:
После дифференцирования по А и к получим два уравнения:
или
(5.1)
Для облегчения расчетов необходимо составить таблицу (табл. 5.1), куда вносятся значения элементов уравнения. Для этого используются средние значения (табл. 3.2, 4.1).
Таблица 5.1 Значения элементов уравнения.
| i | yi | xi | Yi=lg yi | Xi=lg xi | YiXi | 
|
| 20,42 | 1,310 | 1,000 | 1,310 | 1,000 | ||
| 34,16 | 1,533 | 1,301 | 1,994 | 1,693 | ||
| 44,44 | 1,648 | 1,477 | 2,434 | 2,181 | ||
| 52,62 | 1,721 | 1,602 | 2,757 | 2,566 | ||
| 61,64 | 1,790 | 1,699 | 3,041 | 2,887 | ||
| 68,04 | 1,833 | 1,778 | 3,259 | 3,161 | ||
| Сумма: | 9,835 | 8,857 | 14,795 | 13,488 |
Подставляем соответствующие значения параметров (табл. 5.1) в уравнения (5.1)
6·А+к·8,857=9,835
А·8,857+к·13,488=14,795 (5.2)
Для возможности решения этих уравнений умножим первое из них на
(-8,857/6).
Тогда:
Или –8,857А-к·13,074=-14,518
Складываем это уравнение со вторым уравнением системы (5.2).
–8,857А-к·13,074=-14,518
А·8,857+к·13,488=14,795
0,000+к·0,414=0,277
Отсюда к=0,277/0,414=0,669
Для нахождения А подставим значения к в одно из уравнений системы 6.2.
6·А+0,669·8,857=9,835
Тогда а=10А=100,652=4,487
Т.о., функциональная зависимость в частном виде будет иметь вид:
у=4,487·х0,669 (5.3)
После этого производим вычисление для построения на графике математической кривой:
у1=4,487·100,669=20,94
у2=4,487·200,669=33,29
у3=4,487·300,669=43,67
у4=4,487·400,669=52,94
у5=4,487·500,669=61,46
у6=4,487·600,669=69,43
На основании этих вычислений строим график (рис. 5.1).
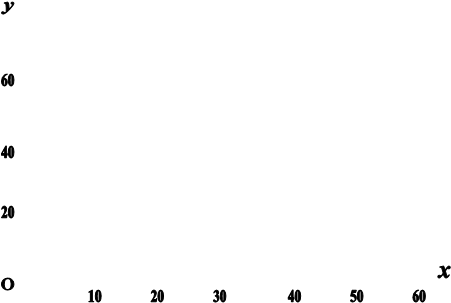
Рисунок 5.1 – График зависимости y=f(x), полученный на основании выражения (5.3).
На этот же график наносим результаты экспериментальных исследований (каждые пять точек у для всех значений х), (табл. 3.2).
Далее задача сводится к построению доверительного интервала.
6 определение доверительного интервала
Построение доверительного интервала и, следовательно, определение доверительной вероятности позволяет оценить степень надежности полученного результата.
Математическое описание доверительного интервала для отдельно взятой точки выражается следующим образом:
(6.1)
где у – истинное значение измеряемой величины;
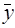– среднее арифметическое значение, полученное в результате
измерений;
Δу – погрешность измерения у.
Вероятность α носит название доверительной вероятности или коэффициента надежности.
Интервал значений от 
до 
называется доверительным интервалом, т.е. интервалом, в который попадает истинное значение у с заданной вероятностью.
Чем больше величина доверительного интервала, т.е. чем больше задаваемая погрешность измерений Δу, тем с большей надежностью искомая величина у попадает в этот интервал.
Величина надежности α зависит от числа измерений n произведенных измерений, а также от величины задаваемой погрешности. На практике число измерений всегда ограничено и поэтому, чтобы получить объективную оценку границ доверительного интервала для у, интервал Δу представляется в виде:
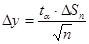
Откуда 
или 
Коэффициент tα предложен в 1908 году английским математиком и химиком В.С. Госсетом, публиковавшем свои работы под псевдонимом «Стьюдент» - студент, и получил в последствие название коэффициента Стьюдента.
С учетом этого коэффициента выражение (6.1) примет вид:
(6.2)
В таблице (6.1) приведены значения коэффициентов Стьюдента tα для разных значений надежности α при разных значения n. Считается, что при обычных измерениях можно ограничиться доверительной вероятностью 0,90 или 0,95. Для измерений, по условиям которых требуется чрезвычайно высокая степень надежности, задают доверительную вероятность 0,999. Т.о. на практике пользуются интервалом доверительной вероятности, лежащим в пределах 0,9…0,999.
Таблица 6.1 Значения коэффициентов Стьюдента.
| n-1 | Значение α | ||||
| 0,90 | 0,95 | 0,98 | 0,99 | 0,999 | |
| 6,31 | 12,7 | 31,8 | 63,7 | 63,66 | |
| 3,92 | 4,3 | 6,96 | 9,92 | 31,6 | |
| 3,25 | 3,18 | 4,54 | 5,84 | 12,9 | |
| 2,13 | 2,78 | 3,75 | 4,60 | 8,61 | |
| 2,02 | 2,57 | 3,36 | 4,03 | 6,87 | |
| 1,94 | 2,458 | 3,14 | 3,71 | 5,96 | |
| 1,89 | 2,36 | 3,00 | 3,50 | 5,41 | |
| 1,86 | 2,31 | 2,90 | 3,36 | 5,04 | |
| 1,83 | 2,26 | 2,82 | 3,25 | 4,78 |
При рассмотрении доверительного интервала функции в целом вычисляются доверительные интервала для а и к, эта задача является гораздо сложней. Для ее решения разработана соответствующая методика.
Чтобы упростить выполнение работы, рассмотрим лишь доверительные интервалы у двух соседних точек (например, при х=30 и х=40).
По (2.1, 2.2 и с учетом табл. 4.2) вычисляем среднеквадратичные ошибки:
Задаемся α=0,95 и по таблице 6.1 находим коэффициент Стьюдента.
tα =2,78
тогда по (6.2):
44,44-2,78·1,604<у< 44,44+2,78·1,604
или 39,98<у<48,90;
52,62-2,78·2,694<у<52,62+2,78·2,694
или 45,13<у<60,11
Эти граничные значения у наносим на график (рис. 5.1) и соединяем две верзние и нижние точки, получаем в графическом виде доверительный интервал для заданного участка кривой.
В заключение произведем оценку точности измерений. Для этого вводится понятие относительной погрешности ε, равной отношению абсолютной погрешности Δу результата измерений к результату измерений у.
Обычно эта погрешность выражается в процентах.
(6.3)
Для нашего случая:
Из приведенных вычислений следует, что измерения у при х=40 имеют более высокую погрешность, а точность измерений недостаточно высока (удовлетворительная погрешность результата измерений не должна превышать 10%).
7 вопросы для самопроверки и контроля знаний.
1. Основные источники ошибок.
2. Классы ошибок.
3. Природа систематических и случайных ошибок.
4. Основные положения теории ошибок.
5. Что сделано Гауссом касательно теории ошибок?
6. Среднеквадратичная ошибка отдельного измерения и средняя квадратичная погрешность результата серии измерений.
7. Что такое промах?
8. Технология исключения промахов.
9. Четыре вида зависимости между переменными.
10. Суть регрессионного и корреляционного методов анализа
11. Какими показателями характеризуются тесноты связи между переменными.
12. Как распознается функциональная зависимость результатов измерений.
13. Суть метода наименьших квадратов.
14. Зачем нужен метод выравнивания и в чем он заключается?
15. Что такое доверительная вероятность?
16. Что такое коэффициент Стьюдента и какое его назначение? Кто ввел этот коэффициент?
17. Технология определения доверительного интервала.
18. Какая разница между абсолютной и относительной погрешностями измерений?
При сдаче зачета по дисциплине в целом студент должен ответить и на ниже приведенные вопросы:
1. Значение эксперимента в науке.
2. Принцип действия светолучевого осциллографа.
3. Устройство гальванометра.
4. Принцип действия самопишущего прибора.
5. В каких случаях применяются самопишущие приборы и осциллографы.
6. Тензодатчики. Устройство и принцип действия. В каких случаях применяются рольговые датчики?
7. Технология наклейки тензодатчиков.
8. Соединение тензодатчиков в мостовую схему. Зачем это нужно? В каких случаях используется полумостовая схема сборки?
9. Какая разница между рабочими и компенсационными датчиками?
10. Назначение тензоусилителей и их деление по несущей частоте (низкочастотные и высокочастотные).
11. Комплект аппаратуры при тензометрических измерениях.
12. Зачем нужны экранированные соединительные провода?
13. Что такое тарировка и зачем она нужна?
14. Разница между прямой и косвенной тарировкой?
15. Основные этапы тарировки. Запись осциллограммы, построение графика, определение масштаба записи.
16. Основные виды датчиков для измерения усилий.
17. Датчики для измерения крутящих моментов.
18. Датчики для измерения перемещений.
19. Датчики для перемещения скоростей.
20. Датчики для измерения ускорений.
21. Виброметры и их назначение.
22. Датчики для измерения давления в гидросистемах.
23. Способы измерения электрических параметров: тока, напряжения и мощности.
24. Что такое планируемый эксперимент и случаи, в которых его использование необходимо?
25. Что такое «черный ящик» и его сущность?
26. Факторный эксперимент. Суть и виды.
27. Графическое изображение плана двух- и трехфакторного планируемого эксперимента.
28. Необходимость кодирования факторов.
29. Что нужно составить для планирования эксперимента?
30. В чем заключается суть операции «движение к области оптимума»?
литература
Основным источником при изучении вышеперечисленных вопросов является книга:
Жук А.Я., Желябина Н.К. Теория и практика приводов. Учебн. пос. в 3-х кн. Кн.3 / Запорожье: Издательство ЗГИА, 2001 – 176 с.
контрольная работа
Дата добавления: 2015-07-20; просмотров: 87 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение | | | Требования к оформлению контрольной работы |