О.Ю. Ермолаев классифицирует непараметрические критерии по решаемым задачам.

Первая группа: непараметрические критерии для несвязанных выборок: критерий U Манна – Уитни, критерий Q Розенбаума, Н-критерий Крускала – Уоллиса, S-критерий тенденций Джонкира и др.

Вторая группа: непараметрические критерии для связанных выборок. К ним относятся: критерий знаков G, парный критерий Т Вилкоксона, критерий Фридмана, критерий тенденций Пейджа, критерий Макнамары и др.

Третья группа: критерии согласия распределений (χ² и критерий Колмогорова – Смирнова) и многофункциональный критерий φ.

Рассмотрим возможности непараметрических критериев для несвязанных выборок.

1. Самым мощным аналогом t-критерия Стьюдента является критерий U Манна – Уитни (Mann – Whitney U). Этот критерий применяют для оценки различий по уровню выраженности какого-либо признака для двух независимых (несвязанных) выборок. При этом выборки могут различаться по числу входящих в них испытуемых. Особенно удобен в том случае, когда число испытуемых невелико и в обеих выборках не превышает величину 20, хотя разработаны таблицы критических значений, рассчитанные для большего количества величин выборок – до 60 человек испытуемых (О.Ю. Ермолаев). Оценивает степень пересечения рядов значений измеренного признака. Как правило, проводится ранжирование, затем вычисляются суммы рангов, и определяется наибольшая ранговая сумма (R_max). Затем вычисляются значения U_эмп по формуле:

U_эмп = n₁*n₂+(n_х*(n_х+1)/2)-R_max, (20)

где n_х – количество испытуемых в группе с большей суммой рангов, где n₁ – объём выборки 1, n₂ – объём выборки 2, а R_max – наибольшая по величине сумма рангов. Если по специальным формулам подсчитаны значения U_х и U_y (для выборок Х и Y по отдельности), то в качестве эмпирического значения критерия берётся меньшее из U_х и U_y. Чем больше различия, тем меньше эмпирическое значение U. Соответственно, значение р-уровня тоже будет меньше, на что необходимо обращать внимание при интерпретации.

О.Ю. Ермолаев отмечает, что критерий U применяют и для связных выборок, рассматривая их как независимые, если связи внутри генеральной совокупности оказываются слабыми, а различия – сильными. В этом случае другие критерии могут оказаться менее мощными.

2. Критерий Q Розенбаума. Этот критерий существенно проще, чем критерий U, и применяется для малых выборок. Он основан на сравнении двух упорядоченных, но не обязательно равных по численности рядов наблюдений. Работа с критерием Розенбаума предполагает подсчет так называемых «хвостов» (величина «хвостов» равна числу элементов ряда, которые находятся левее (правее) начала совпадающих элементов ряда). Потому этот критерий имеет также название «критерий хвостов». Если в выборке отсутствуют «хвосты», критерий Q неприменим, следует воспользоваться критерием Манна – Уитни. Измерение должно проводиться по шкале порядка, интервальной или отношений. Выборки должны быть независимыми. Количество испытуемых – от 11 до 26 человек. При числе наблюдений, превышающем 26 человек, О.Ю. Ермолаев предлагает пользоваться следующими величинами Q_крит.: Q_крит.=8 для р≤0,05, Q_крит.=10 для р≤0,05. Критерий вычисляется как сумма «хвостов»: Q_эмп.=S+Т, где S и Т – величины правого и левого «хвостов». Когда сумма S и Т достаточно велика, различия будут значимыми.

3. Н-критерий Крускала – Уоллиса (Kruskal – Wallis H) является непараметрическим аналогом однофакторного дисперсионного анализа (ANOVA) для независимых выборок, поэтому А.Д. Наследов приводит другое его название: «однофакторный дисперсионный анализ Крускала – Уоллиса» (Kruskal – Wallis one way analysis of variance). Критерий Н применяется для оценки различий по степени выраженности анализируемого признака одновременно между тремя, четырьмя и более выборками. Н-критерий Крускала – Уоллиса по идее сходен с критерием U Манна – Уитни. Он оценивает степень пересечения рядов значений измеренного признака. Все значения выборок представляются в виде одной общей последовательности упорядоченных (ранжированных) значений с последующим вычислением среднего ранга для каждой из выборок. Если различий нет, все ранги окажутся близки к общему среднему рангу:

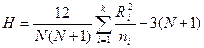, (21)

где R – ранг каждого i-ного числа, N – количество элементов выборки.

Измерение предполагает шкалу порядка, интервалов или отношений. Выборки должны быть независимыми. Допускается разное число испытуемых в выборках. При сопоставлении трёх выборок, допускается, чтобы в одной из них было 3, а в двух других по 2 наблюдения при максимальном р-уровне р≤0,05. Таблицы разработаны только для трёх выборок с максимальным числом наблюдений не более 5. Для большего числа выборок и при разном количестве испытуемых применяются таблицы для критерия 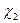. Число степеней свободы при этом определяется как разность с-1, где с – число сопоставляемых выборок (О.Ю. Ермолаев). Н-критерий позволяет выявить степень изменения признака в выборках, не указывая, однако, на направление этих изменений. Для утверждения о том, что уровень выраженности признака в какой-то из сравниваемых выборок выше или ниже, необходимо парное соотнесение выборок по критерию U Манна – Уитни.

4. S-критерий тенденций Джонкира. Ориентирован на выявление тенденций изменения измеряемого признака при сопоставлении от трёх до шести выборок. В отличие от предыдущего критерия Н, количество элементов в каждой выборке должно быть одинаковым. Если число элементов в каждой выборке различно, необходимо случайным образом уравнять выборки, при этом неизбежно утрачивается часть информации. Если потери информации необходимо избежать, то следует воспользоваться вышеприведенным критерием Н Крускала – Уоллиса, однако в этом случае нельзя будет выдвигать гипотезу о наличии или отсутствии тенденций.

Нижняя граница применимости – три выборки, каждая из которых включает не менее двух элементов. Верхняя граница – 6 выборок, включающих не более 10 элементов каждая. При большем количестве также применяется критерий Н.

Критерий S основан на следующем принципе: все выборки располагаются слева направо в порядке возрастания значений исследуемого признака. После упорядочивания для каждого отдельного элемента, стоящего слева в выборке, подсчитывается число инверсий по отношению ко всем элементам упорядоченных выборок, расположенных правее. Инверсией для данного элемента выборки считается число элементов, которые превышают данный элемент по величине по всем выборкам справа. Инверсии по отношению к собственной выборке, в которой находится данный элемент, не подсчитываются. В соответствии с этим правилом у последнего столбца выборки инверсии также не подсчитываются, так как справа больше нет данных. Правило подсчета инверсий позволяет утверждать, что чем выше величина инверсий у крайних правых столбцов, тем выше уровень значимости статистики S. Подробнее с алгоритмом расчёта можно познакомиться в справочных пособиях О.Ю. Ермолаева, Е.В. Сидоренко и др.

Обобщим результаты анализа непараметрических критериев для исследования различий признаков, измеренных на несвязанных выборках, с помощью алгоритма на рисунке 11.

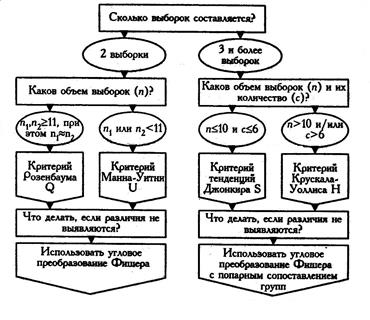
Рис. 11. Алгоритм принятия решения о выборе критерия для сопоставлений (по Е.В. Сидоренко)

Далее рассмотрим возможности непараметрических критериев различий для связанных выборок.

1. Критерии знаков G относится к непараметрическим критериям и применяется только для связанных (зависимых) выборок. Он дает возможность установить, насколько однонаправленно изменяются значения признака при повторном измерении связанной, однородной выборки. Критерий знаков применяется к данным, полученным в ранговой, интервальной шкалах и шкале отношений. Для каждого измерения отдельно определяют величину «сдвига», то есть изменения между первым и вторым измерением. Важно учитывать знак, то есть направление каждого изменения. Затем подсчитываются суммы нулевых, положительных и отрицательных сдвигов. Сумма нулевых сдвигов отбрасывается, сумма ненулевых сдвигов показывает, насколько изменяются значения признака и в какую сторону – уменьшения или увеличения. Для этого наибольшая из сумм определяется как величина типичного сдвига (n), а наименьшая – как нетипичный (G_эмп) Обратим внимание, что чем больше количество нетипичных сдвигов, тем меньше вероятность статистической значимости различий. К подобным исключениям относятся также парный критерий Т Вилкоксона, критерий U Манна – Уитни, критерий Макнамары. В случае, когда типичный и нетипичный сдвиги равны, критерий G неприменим.

2. Парный критерий Т Вилкоксона (Wilcoxon signed-rank test). Непараметрическим аналогом критерия является критерий знаков. Измерение может быть проведено в ранговой, интервальной шкалах и шкале отношений. Парный критерий Т Вилкоксона является более мощным, чем критерий знаков, и применяется для оценки различий экспериментальных данных, полученных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет выявить не только направленность изменений, но и их выраженность, установить, насколько сдвиг показателей в каком-то одном направлении является более интенсивным, чем в другом. Основан на упорядочивании величин разностей (сдвигов) значений признака в каждой паре его измерений (сравним: критерий знаков основывается только на учёте знака этой разности). Ранжирование абсолютных величин означает, что знаки разностей не учитываются, однако в дальнейшем, наряду с общей суммой рангов, находится отдельно сумма рангов как для положительных, так и для отрицательных сдвигов. Идея заключается в подсчёте вероятности получения минимальной из разностей при условии, что распределение положительных или отрицательных разностей равновероятно и равно ½. Если интенсивность сдвига в одном из направлений оказывается большей, то соответствующая сумма рангов также оказывается больше. Этот сдвиг называется типичным, а противоположный, меньший по сумме рангов, сдвиг – нетипичным. Как и для критерия знаков эти два сдвига оказываются дополнительными друг к другу. Критерий Т Вилкоксона базируется на величине нетипичного сдвига, который обозначается Т и сравнивается с табличным значением. Критерий принято применять при численности выборки от 5 до 50 человек. Подробнее с алгоритмом расчёта можно познакомиться в справочных пособиях О.Ю. Ермолаева, Е.В. Сидоренко и др.

3. Критерий χ_r² Фридмана (Friedman test). Относится к непараметрическим, поскольку основан на процедуре ранжирования, однако применим только к данным, измеренным в шкале интервалов или отношений. А.Д. Наследов определяет критерий χ_r² Фридмана как непараметрический аналог однофакторного дисперсионного анализа (ANOVA) для повторных изменений. Критерий Фридмана можно рассматривать как распространение критерия Т Вилкоксона на три и большее количество измерений связанной выборки испытуемых. Критерий позволяет установить уровень статистической достоверности различий сразу в нескольких измерениях (от 3 до 100), но не дает возможности выявить направление изменений. Для выявления направления изменений необходимо провести попарное соотнесение выборок по Т-критерию Вилкоксона. При наличии сразу нескольких измерений преимущество критерия Фридмана в том, что он позволяет выявить наличие значимых различий в измерениях за один раз. Условия применения: применим только к данным, измеренным в шкале интервалов или отношений; выборка должна быть связанной; в выборке должно быть не менее 2 испытуемых с не менее чем 3 показателями, максимальное количество измерений не может превышать 100. Подробнее с алгоритмом расчёта можно познакомиться в справочных пособиях О.Ю. Ермолаева, Е.В. Сидоренко и др.

4. Критерий Пейджа (его полное название L-критерий тенденций Пейджа) можно рассматривать как эквивалент критерия Фридмана для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испытуемых. Однако этот критерий не только позволяет выявить различия, но и указывает на направление в изменении величин признака. Если критерий Фридмана выявляет наличие различий в измеренных показателях (признаках), то критерий Пейджа позволяет выявить тенденцию в изменениях величин измеряемых признаков. Именно поэтому он является более предпочтительным. Измерение может быть проведено в ранговой, интервальной шкалах и шкале отношений. Применение этого достаточно мощного критерия ограничено объемом выборки: число испытуемых не может быть менее 2 и больше 12, а число измерений признака не может быть менее трёх и больше 6. Подробнее с алгоритмом расчёта можно познакомиться в справочных пособиях О.Ю. Ермолаева, Е.В. Сидоренко и др.

Выше рассмотрены критерии для работы с данными, измеренными в порядковой, интервальной шкалах и шкале отношений. Рассмотрим возможности подгруппы непараметрических критериев для связанных выборок с измерениями в номинативной шкале на примере критерия Макнамары.

5. Критерий М Макнамары имеет некоторые особенности. Этот критерий относится также к числу непараметрических критериев и предназначен для работы с данными, полученными в самой простой из номинальных шкал – дихотомической. Условия применения: измерение произведено в дихотомической шкале; выборка связанная; первоначальные данные переносятся в таблицу «2х2», поля в которой обозначаются соответственно: А (выборы 0,0), В (выборы 1,0), С (выборы 0,1), D (выборы 1,1). При количестве измерений меньше 20 для определения М_эмп. используется таблица биноминального распределения, а величины М_кр. постоянны и равны 0,025 для 5-процентного уровня значимости и 0,005 для 1-процентного уровня значимости. При количестве измерений более 20 М_эмп. вычисляется по формуле: М_эмп.=(В-С)²/(В+С), где В и С – значения соответствующих полей таблицы «2х2», а величины М_кр. постоянны и равны 0,025 для 5-процентного уровня значимости и 0,005 для 1-процентного уровня значимости. Отметим, что при В=С критерий не применяется, используется критерий χ². Подробнее с алгоритмом расчёта можно познакомиться в справочных пособиях О.Ю. Ермолаева, Е.В. Сидоренко и др.

Обобщим результаты анализа непараметрических критериев для исследования различий признаков, измеренных на связанных выборках, с помощью алгоритма на рисунке 12.

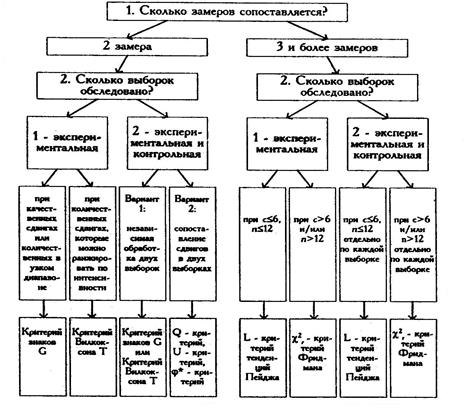
Рис. 12. Алгоритм принятия решения о выборе критерия оценки изменений (по Е.В. Сидоренко)

Далее рассмотрим возможности непараметрических критериев согласия распределений.

Распределения могут различаться по средним, дисперсиям, асимметрии, эксцессу и по сочетаниям этих параметров.

Традиционными для отечественной математической статистики критериями определения расхождения или согласия распределений являются метод χ² К. Пирсона и критерий λ Колмогорова – Смирнова.

Оба этих метода требуют тщательной группировки данных и довольно сложных вычислений. Кроме того, возможности этих критериев в полной мере проявляются на больших выборках (n>30). Тем не менее они могут оказаться незаменимыми в следующих двух случаях:

· в задачах, требующих доказательства неслучайности предпочтений в выборе из нескольких альтернатив;

· в задачах, требующих обнаружения точки максимального расхождения между двумя распределениями, которая затем используется для перегруппировки данных с целью применения критерия φ* (углового преобразования Фишера).

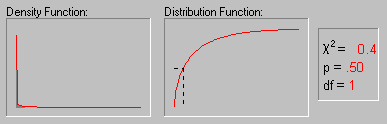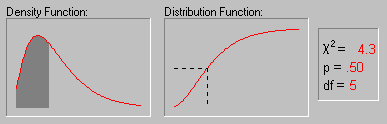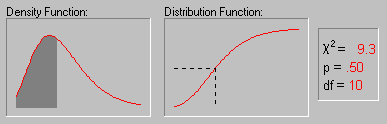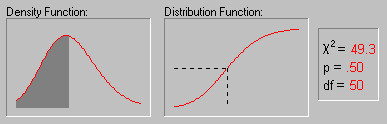
1. Критерий χ² (хи-квадрат) (см. рис. 13) – один из наиболее часто использующихся в психологических исследованиях, поскольку он позволяет решать большое число разных задач, и, кроме того, исходные данные для него могут быть получены в любой шкале, начиная со шкалы наименований. Критерий хи-квадрат используется в двух вариантах:

· как расчет согласия эмпирического распределения и предполагаемого теоретического (в этом случае проверяется гипотеза Н₀ об отсутствии различий между теоретическим и эмпирическим распределениями),

· как расчет однородности двух независимых экспериментальных выборок (в этом случае проверяется гипотеза Н₀ об отсутствии различий между двумя эмпирическими (экспериментальными) распределениями).

an_chi.gif

Рис. 13. Изменение формы χ²-распределения при увеличении числа степеней свободы (1, 2, 5, 10, 25 и 50) (источник: statsoft.ru)

Критерий построен так, что при полном совпадении экспериментального и теоретического распределений χ²=0. Чем больше расхождение между распределениями, тем больше χ². Основная расчетная формула критерия χ² для сравнения двух эмпирических распределений в зависимости от вида представленных данных может иметь следующий вид:

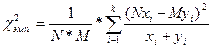, (22)

где N и M – соответственно число элементов в первой и во второй выборке. Эти числа могут совпадать, а могут быть и различными. Для критерия χ² оценка уровней значимости определяется по числу степеней свободы, которое обозначается df или греческой буквой ν (ню) и в большинстве случаев вычисляется по формуле: ν = k - 1, где k каждый раз определяется по выборочным данным и представляет собой число элементов в выборке. Если при расчете критерия используется таблица экспериментальных данных, то величина ν рассчитывается следующим образом: ν = (k - 1)(с - 1), где к – число строк, а с – число столбцов.

Ограничения критерия: объем выборки должен быть достаточно большим (n≥30); если количество разрядов (k) задано заранее, минимальное число наблюдений (n_min) определяется по формуле: n_min =k*5; выбранные разряды должны охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопоставляемых распределениях. Необходимо вносить «поправку на непрерывность» при сопоставлении распределений признаков, которые принимают всего 2 значения. Разряды должны быть неперекрещивающимися. Сумма наблюдений по разрядам должна быть равна общему количеству наблюдений.

2. Критерий λ Колмогорова – Смирнова предназначен для сопоставления двух распределений:

а) эмпирического с теоретическим, например, равномерным или нормальным;

б) одного эмпирического распределения с другими эмпирическим распределением.

Используется для решения тех же задач, что и критерий χ². Однако если при применении χ² мы сопоставляем частоты двух распределений, то в данном критерии сравниваются накопленные (кумулятивные) частоты по каждому разряду (альтернативе). При этом, если разность накопленных частот в двух распределениях оказывается большой, то различия между двумя распределениями являются существенными. Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.

Ограничения критерия λ: выборка должна быть достаточно большой. При сопоставлении двух эмпирических распределений необходимо, чтобы суммарный объём двух выборок был больше 50. Сопоставление эмпирического распределения с теоретическим иногда допускается при меньших выборках. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака. Мы не можем накапливать частоты по разрядам, которые отличаются лишь качественно и не представляют собой шкалы порядка. Во всех случаях, когда разряды представляют собой не упорядоченные по возрастанию или убыванию какого-либо признака категории, нам следует применять метод χ².

Обобщим результаты анализа критериев для сравнения распределений с помощью рис. 14.

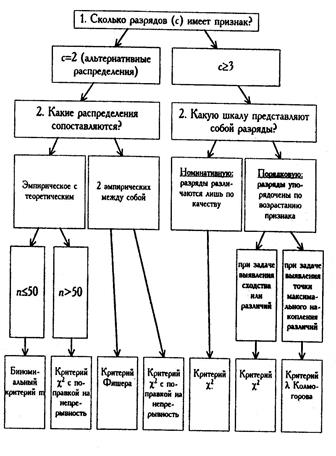
Рис. 14. Алгоритм принятия решения о выборе критерия для сравнения распределений (по Е.В. Сидоренко)

Кроме рассмотренных выше критериев, существуют так называемые многофункциональные критерии.

Многофункциональные статистические критерии – это критерии, которые могут использоваться по отношению к самым разнообразным данным, выборкам и задачам. Данные могут быть представлены в любой шкале, начиная от номинативной (шкалы наименований). Выборки могут быть как независимыми, так и связанными. Нижняя граница выборок – 5 наблюдений, но возможно применение критериев и по отношению к выборкам с n=2 (с некоторыми оговорками). Верхняя граница выборок задана только в биномиальном критерии – 50 человек. В критерии φ* Фишера верхней границы не существует: выборки могут быть сколь угодно большими.

Многофункциональные критерии позволяют решать задачи сопоставления уровней исследуемого признака, сдвигов в значениях исследуемого признака и сравнения распределений.

Алгоритм выбора многофункциональных критериев представлен на рисунке 15.

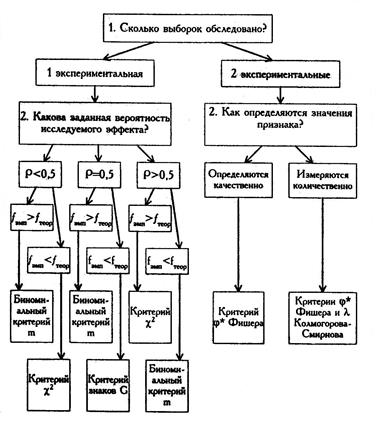
Рис. 15. Алгоритм выбора многофункциональных критериев (по Е.В.Сидоренко)

Многофункциональные критерии построены на сопоставлении частот встречаемости признака, выраженных в долях единицы или в процентах. Суть критериев состоит в определении того, какая доля наблюдений (реакций, выборов, испытуемых) в данной выборке характеризуется интересующим исследователя эффектом, и какая доля этим эффектом не характеризуется.

Эффектом может быть:

a) определенное значение качественно определяемого признака;

б) определенный уровень количественно измеряемого признака;

в) определенное соотношение значений или уровней исследуемого признака.

Путем сведения любых данных к альтернативной шкале «Есть эффект – нет аффекта» многофункциональные критерии позволяют решать все три задачи сопоставлений: сравнения «уровней», оценки «сдвигов» и сравнения распределений.

К числу многофункциональных критериев относится критерий φ* Фишера (угловое преобразование Фишера) и, с некоторыми оговорками, биномиальный критерий m.

1. Критерий Фишера φ* применяется в тех случаях, когда обследованы две выборки испытуемых, биномиальный критерий m – в тех случаях, когда обследована лишь одна выборка испытуемых.

Критерий φ* предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта. Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован эффект. Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол φ*, а меньшей доле – меньший угол, но соотношения здесь не линейные: 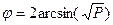, где Р – процентная доля, выраженная в долях единицы. При увеличении расхождения между углами φ₁ и φ₂ и увеличения численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны (рис. 16).

Величины φ₁ и φ₂, соответствующие процентным долям каждой выборки, определяются по таблицам, а эмпирическое значение подсчитывается по формуле:

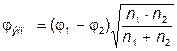, (23)

где φ₁ и φ₂ – табличные величины, соответствующие большей и меньшей процентным долям; n₁ и n₂ – количество наблюдений в первой и второй выборках.

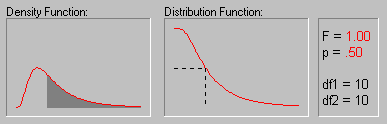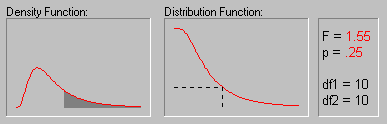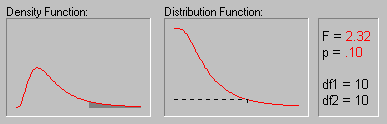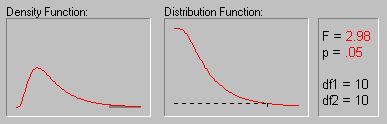
an_fdist.gif

Рис. 16. Значения вероятностей для F-распределения (степени свободы равны 10) (источник: statsoft.ru)

Ограничения критерия φ*: ни одна из сопоставляемых долей не должна быть равной нулю; верхний предел в критерии φ отсутствует; нижний предел – 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок: если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30; если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7; если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5; при n₁,n₂≥5 возможны любые сопоставления.

В принципе возможно и сопоставление выборок, не отвечающих этому условию, например, с соотношением n₁=2, n₂=15, но в этих случаях не удастся выявить достоверных различий. Подробнее с алгоритмом расчёта можно познакомиться в справочных пособиях О.Ю. Ермолаева, Е.В. Сидоренко и др.

2. Биномиальный критерий m предназначен для сопоставления частоты встречаемости какого-либо эффекта с теоретической или заданной частотой его встречаемости. Он применяется в тех случаях, когда обследована лишь одна выборка объемом не более 300 наблюдений, в некоторых задачах – не больше 50 наблюдений. Позволяет оценить, насколько эмпирическая частота интересующего нас эффекта превышает теоретическую, среднестатистическую или какую-то заданную частоту, соответствующую вероятности случайного угадывания, среднему проценту успешности в выполнении данного задания, допустимому проценту брака и т. п.

Биномиальный критерий незаменим, если: обследована лишь одна выборка испытуемых и нет возможности или смысла делить эту выборку на две части с целью дальнейшего применения критерия φ*, так как для нас по каким-то причинам важно исследовать частоту встречаемости признака в выборке в целом; в обследованной выборке менее 30 испытуемых, что не позволяет нам применить критерий χ².

Ограничения биномиального критерия: в выборке должно быть не менее 5 наблюдений; верхний предел численности выборки варьируется в диапазоне от 50 до 300 наблюдений, что определяется имеющимися таблицами критических значений; критерий m позволяет проверить лишь гипотезу о том, что частота встречаемости интересующего нас эффекта в обследованной выборке превышает заданную вероятность Р. Заданная вероятность при этом должна быть не более 0,50 (Р ≤0,50). Если мы хотим проверить гипотезу о том, что частота встречаемости интересующего нас эффекта достоверно ниже заданной вероятности, то при Р=0,50 мы можем сделать это с помощью уже известного критерия знаков G, при Р>0,50 мы должны преобразовать гипотезы в противоположные, а при Р<0,50 придется использовать критерий χ². Подробнее с алгоритмом расчёта можно познакомиться в справочных пособиях О.Ю. Ермолаева, Е.В. Сидоренко и др.

Многофункциональные критерии могут применяться как эффективные заменители традиционных критериев. В тех случаях, когда обследованы две выборки испытуемых, критерий φ* может эффективно заменять или, по крайней мере, эффективно дополнять традиционные критерии: Q-критерий Розенбаума, U-критерий Манна – Уитни, критерий χ² Пирсона и критерий λ Колмогорова – Смирнова.

В особенности полезна такая замена в случаях, если: другие критерии неприменимы; другие критерии неэффективны или слишком громоздки; другие критерии слишком трудоемки. Последний случай чаще всего относится к критерию χ². Заменить его критерием φ* можно при условии, если сравниваются распределения признака в двух выборках, а сам признак принимает всего два значения.

Примеры проверки прикладных гипотез с применением критериев значимости мы рассмотрим на практическом занятии. Отработать навыки расчётов можно с помощью лабораторной работы.

Дата добавления: 2015-07-20