Лекция № 9 расчёт на прочность основных элементов турбин

Статический изгиб рабочих лопаток

Рабочее тело воздействует на рабочие лопатки усилием, представляющим собой распределённую нагрузку, которая в общем случае изменяется по длине лопатки. Лопатка без бандажа и бандажной проволоки рассматривается как консольная балка переменного профиля, нагруженная распределённой нагрузкой q (x) (рис. 15.1).

Уравнения для моментов М_z и М_y, изгибающих лопатку в направлении z и y, могут быть записаны в следующей форме:

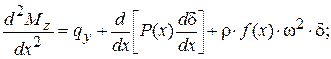(15.1)

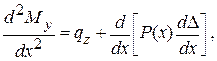(15.2)

где q_y и q_z – составляющие аэродинамической нагрузки q (x); d, D – смещения оси лопатки от положения равновесия за счёт прогиба в направлении y и z соответственно.

Таким образом, изгибающие моменты в сечении x зависят не только от аэродинамических сил q (x), но и от центробежных сил P (x) и от прогиба лопатки, определяемого смещениями d и D.

Составляющие аэродинамической силы q_y и q_z можно определить, если известны скорости рабочего тела в ступени:

(15.3)

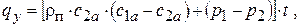(15.4)

где r_п – плотность рабочего тела в рабочей решётке; t – шаг решётки; p ₁ и p ₂ – давление перед рабочей решёткой и за ней.

Напряжения, возникающие в сечении х при изгибе рабочей лопатки, определяются известным соотношением:

, (15.5)

где М _x и М _h - изгибающие моменты относительно центральных главных осей x и h (рис. 1.); J _x, J _h - моменты инерции профиля относительно этих осей. С моментами М_z и М_y они связаны так:

М _h = - М_y ×cosg + М_z ×sing; (15.6)

М _x = М_y ×sing + М_z ×cosg. (15.7)

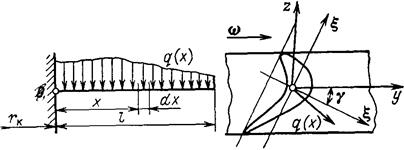
Рис. 1. Схема нагружения лопатки изгибающими усилиями

На входной и выходной кромках профиля напряжения растяжения от статического изгиба и центробежных сил складываются, и в этих точках возникают наибольшие статические напряжения растяжения.

Проектируя лопатку, нужно так выбрать хорду профиля, чтобы наибольшие напряжения были равны допустимым.

Пусть уже выбран модельный профиль, для которого известны хорда b _м, шаг t _м и моменты инерции J _xм и J _hм. Отношение хорд реального и модельного профилей лопатки a назовём масштабным коэффициентом: a = b / b _м. При геометрически подобном изменении решётки все линейные размеры меняются пропорционально a, а моменты инерции – пропорционально четвёртой степени a. Пусть 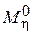и – моменты, действующие на все лопатки ступени:

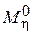= М _h× z; = М _x× z. (15.8)

Подставляя (15.8) в (15.5) и учитывая, что z = 2×p× r / t, получаем:

, (15.9)

где h_м, x_м – координаты точки модельного профиля, в которой возникают наибольшие напряжения изгиба.

Отсюда масштабный коэффициент a можно определить:

. (15.10)

В относительно коротких лопатках (d _ср/ l ³ 5) наибольшие напряжения возникают в корневом сечении, поэтому расчёт следует проводить для r = r _к. В лопатках большей длины максимальные изгибающие напряжения могут возникать и не в корневом сечении. В этом случае расчёт a проводят для наиболее напряжённого сечения.

Если лопатки перевязаны бандажом или проволокой, то изгибающий момент, действующий на перо лопатки, уменьшается за счёт того, что часть изгибающей нагрузки воспринимается бандажом или проволокой. При абсолютно жёстком бандаже можно снизить напряжения от изгиба в пере лопатки примерно на одну треть.

Если ось лопатки прямолинейна и установлена радиально, то при изгибе лопатки центробежные силы будут стремиться вернуть лопатку в положение равновесия, т.е. противодействовать силам, стремящимся изогнуть лопатку. Расчёты показывают, что для лопаток первых и промежуточных ступеней уменьшение изгибающих напряжений за счёт центробежных сил составляет не более 10% и обычно не учитывается. Для длинных лопаток влияние центробежных сил на статический изгиб заметно и учитывается в расчётах.

Дата добавления: 2015-07-20