Курсовая работа. Министерство образования и науки

Министерство образования и науки

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Санкт-Петербургский государственный технологический

университет растительных полимеров»

Кафедра: «Теплосиловые установки и тепловые двигатели»

Курсовая работа

Тема: «Расчет многоступенчатой противодавленческой турбины с регулирующей двухвенечной ступенью скорости».

Вариант №13

Выполнил: студент Рузанова Е.А. Учебная группа: 6-441

Проверил: доцент Коновалов П.Н.

Санкт-Петербург

2012 г.

Введение

В настоящее время и в ближайшей перспективе большая часть электроэнергии будет вырабатываться тепловыми (ТЭС) и атомными (АЭС) электростанциями, основным из которых, преобразующими тепловую энергию в электрическую, является паровая турбина, связанная с электрическим генератором.

Паровые турбины, как наиболее экономичные тепловые двигатели, широко применяются как в большой энергетике, так и в энергетике многих отраслей промышленности.

Современная мощная энергетическая турбина-это сложнейшая машина, состоящая из десятков тысяч деталей. Многие из них работают в очень сложных условиях, подвергаясь воздействию разных, в том числе динамических, неустановившихся сил

Турбина вместе с электрогенератором - турбоагрегат-это только часть турбоустановки, включающей много различных аппаратов и машин. Сама же турбоустановка тесно связана с паропроизводящей частью электростанции – с котлом, парогенератором, ядерным реактором. Все эти аппараты и машины взаимозависимы.

Только правильная эксплуатация паровой турбины, всей турбоустановки, которая включает пуск, и нормальное обслуживание, и остановку, позволяет электростанции бесперебойно, согласно графику и указаниям диспетчерской службы энергосистемы вырабатывать электрическую и тепловую энергию, делать это надёжно для всех элементов электростанции и с наименьшим расходом топлива.

При выполнении курсового проекта преследуются следующие цели:

1) закрепление и углубление знаний, полученных при изучении теоретического курса;

2) приобретение навыков практического применения теоретических знаний при выполнении конкретной инженерной задачи - разработке эскизного проекта многоступенчатой паровой турбины;

3) привитие инженерных навыков при пользовании справочной литературы, атласами профилей решёток турбин, заводскими расчётами и чертежами;

4) использование вычислительной техники в практической работе.

Исходные данные:

- Номинальная электрическая мощность N_эн=18 МВт;

- Частота вращения ротора турбины n=3000 об/мин;

- Давление пара перед стопорным клапаном турбины Р_о=2,2 МПа;

- Начальная температура пара t_o=450°С;

- Давление пара за выходным патрубком турбиной Р_к=0,68 МПа;

- Скорость потока пара перед 1-м сопловым аппаратом турбины С_о=54 м/с.

Предварительный расчет теплового процесса турбины:

1. Определяем располагаемый теплоперепад без учета потерь давления в стопорном и регулирующем клапанах, для чего строим адиабатный процесс расширения в h-s диаграмме и определяем конечные и начальные значения энтальпий:

H_o=i_o-i_кt=3355-3018=337 кДж/кг.

2. Потери давления в стопорном и регулирующем клапанах принимаем: ΔР_к=0,04∙Р_о=0,04∙2,2=0,088 МПа.

3. Давление пара перед сопловыми решетками регулирующей ступени:

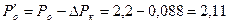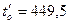МПа, °С.

4. Потери давления в выхлопном патрубке:

;

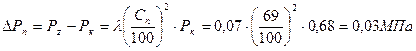где С_п – скорость пара за выходным патрубком;

λ – опытный коэффициент.

5. Давление пара за последней ступенью:

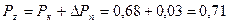МПа.

6. Потери энергии в стопорном и регулирующем клапанах:

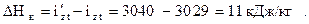
7. Потери энергии в выходном патрубке:

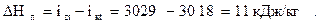
8. Располагаемый теплоперепад на проточную часть:

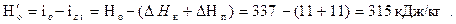
9. Относительный внутренний КПД:

;

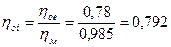где η_ое-относительный эффективный КПД;

η_м-механический КПД.

10. Использованный (внутренний) теплоперепад:

.

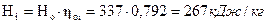11. Относительный внутренний КПД проточной части турбины:

.

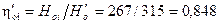12. Откладываем величину Н_i от точки 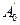на изоэнтропе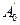 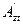, и при энтальпии на пересечении с изобарами Р_к и Р_z, получаем точки A_к и A_z, характеризующие состояние пара за выходным патрубком и за последней ступенью;

i_z=i_o-H_i=3355-267=3088 кДж/кг.

13. Секундный расход пара:

;

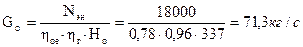где η_г – КПД генератора.

14. Предварительный тепловой процесс турбины:

Расчет регулирующей ступени:

1. Примем h_от1= h_от2=50 кДж/кг, тогда:

.

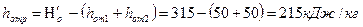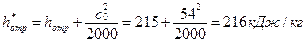
2. Фиктивная скорость в регулирующей ступени:

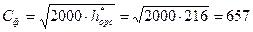м/с.

3. Оптимальное отношение скоростей в регулирующей ступени:

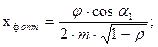
где m=2,число венцов регулирующей ступени;

α₁ – угол выхода потока пара из сопловой решетки, предварительно принимаем 12°;

φ=0,96 - коэффициент скорости, зависит от скорости и характеристик сопла, принимаем;

ρ = 0,1- степень реактивности ступени, принимаем;

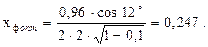
4. Окружная скорость:

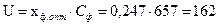м/с.

5. Средний диаметр регулирующей ступени:

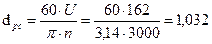м.

6. Фиктивная скорость в нерегулируемой ступени:

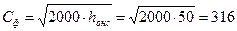м/с.

7. Оптимальное отношение скоростей в нерегулируемой ступени:

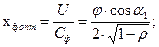
где α₁ – угол выхода потока пара из сопловой решетки, принимаем 17°;

φ=0,96 - коэффициент скорости, принимаем;

ρ = 0,05 - степень реактивности ступени, принимаем;

.

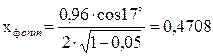8. Окружная скорость на среднем диаметре в нерегулируемой ступени:

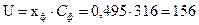м/с.

9. Средний диаметр нерегулируемой ступени:

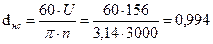м.

10. Степень реактивности регулирующей ступени состоит:

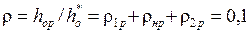
где 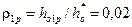степень реактивности в первой рабочей решетке;

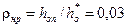степень реактивности в поворотной решетке;

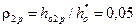степень реактивности во второй рабочей решетке.

11. Располагаемый теплоперепад в сопловой решетке:

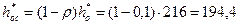кДж/кг.

12. Располагаемый теплоперепад в первой рабочей решетке:

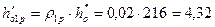кДж/кг.

13. Располагаемый теплоперепад в направляющей решетке:

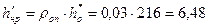кДж/кг.

14. Располагаемый теплоперепад во второй рабочей решетке:

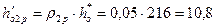кДж/кг.

15. Энтальпия пара по заторможеным параметрам на входе в сопловый аппарат:

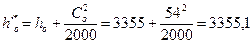кДж/кг.

16. Параметры заторможенного потока из i-s диаграммы:

.

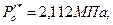
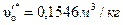17.Откладываем на изоэнтропе 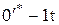теплоперепады: 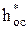; ; 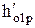; 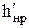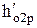(рис.2) и определяем давления:

– за сопловой решеткой: Р₁=1,116 МПа, υ_1t=0,2537 м³/кг,

при h_1t = h₀*- 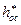= 3355,1– 194,4= 3161 кДж/кг;

– за первой рабочей решеткой: Р₂=1,096 МПа,

при h = h₀*- 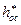-h_о1р´ = 3355,1– 194,4 – 4,32 =3156кДж/кг;

– за поворотной решеткой: ,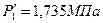

при h = h₀*- 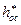-h_о1р´ - h_оп´ = 3355,1–194,4–4,32– 6,48=3150 кДж/кг;

– за второй рабочей решеткой: ,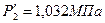

при h = h₀*- 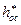-h_о1р´ - h_оп´ - h_о2р´ = 3355,1–194,4–4,32– 6,48-10,8=

=3139 кДж/кг.

18. Отношение давлений в сопловой решетке:

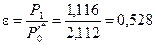
19. Теоретические скорости потока пара и звука на выходе из сопловой решетки:

;

.

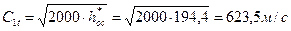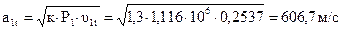20. Число Маха за сопловой решеткой:

.

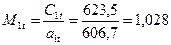21. Утечки пара через переднее концевое уплотнение: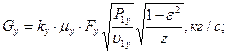

где μ_y=0,8 - коэффициент расхода, зависящий от толщины и конструкции гребня уплотнения и величины радиального зазора;

k_y=1,78 -коэффициент учитывается для уплотнения с гладким валом, зависит от отношения δ_у/s;

δ_у/s=0,05 - принимаем;

s – расстояние между гребнями;

F_у=π·d_у·δ_у=3,14·0,44·0,0003=0,000415 м² - кольцевая площадь радиального зазора;

ε =Р_2у/Р_1у – отношение давлений пара за и перед уплотнением;

Р_1у =Р₁=1,116 МПа, Р_2у=0,1 МПа (атмосферному);

υ₀= υ_1t=0,2537 м³/кг;

z=50, число гребней уплотнения, принимаем;

.

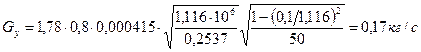22. Утечки пара через заднее концевое уплотнение:

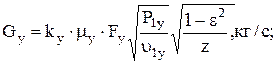
где k_y=1,76 - коэффициент учитывается для уплотнения с гладким валом, зависит от отношения δ_у/s;

δ_у/s=0,05 (принимаем);

ε=Р_2у/Р_1у – отношение давлений пара за и перед уплотнением;

Р_1у =Р_z=0,71 МПа, Р_2у=0,1 МПа (атмосферному);

υ₁= υ_z=0,3756 м³/кг;

z=32 - число гребней уплотнения, принимаем;

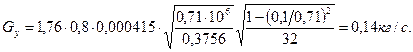
При заданных геометрических соотношениях длины проточных частей

уплотнений будут равны: переднего ;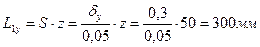

заднего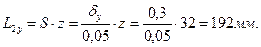

23. Количество пара проходящего через сопло с учетом утечки пара через переднее концевое уплотнение:

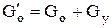=71,3+0,17=71,47 кг/с.

24. Выходная площадь сопловой решетки:

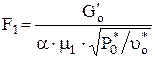,м²;

где μ₁=0,975 – коэффициент расхода, принимаем;

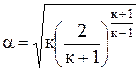-постоянная величина, для перегретого пара равна 0,667 при к=1,3;

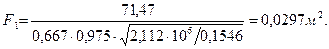
25. Находим произведение:

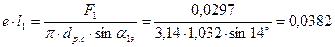м=3,82 см.

26.Оптимальная степень парциальности:

.

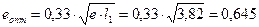27. Длина сопловой лопатки:

.

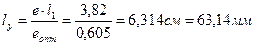28. С учетом ранее принятого α_1э=14° и полученного числа 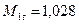выбираем из таблиц типовых сопловых лопаток С-90-15Б со следующими характеристиками: относительный шаг решетки 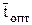=0,78; хорда табличного значения b_т=5,2 см; В=4,0 см; радиус закругления выходной кромки r₂=0,03см; хорда b_с=5см.

29. Число каналов (лопаток) сопловой решетки:

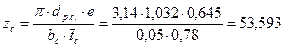принимаем 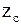=54.

30. Пересчитываем хорду:

.

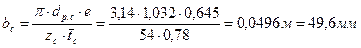31. Относительная толщина выходной кромки:

.

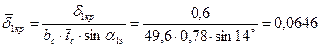32. Относительная длина лопатки:

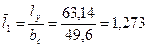; по отношению 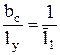=0,786 в соответствии с графиком зависимости μ₁=f(b_с/l₁), коэффициент μ₁=0,978.

уточняем выходную площадь сопловой решётки:

;

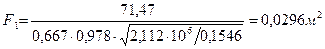уточняем произведение:

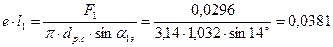м=3,81см;

уточняем оптимальную степень парциальности:

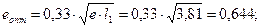
33. Критическое давление:

.

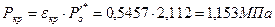34. Откладываем Р_кр на теоретическом процессе (рис.2) и находим параметры пара: i_кр=3170 кДж/кг; υ_кр=0,2475 м³/кг.

35. Критическая скорость:

.

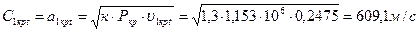36. Поскольку решетка выбрана суживающаяся то при сверхзвуковом обтекании ее необходимо найти угол отклонения потока в косом срезе:

;

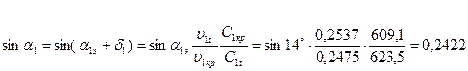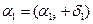=14,02°; 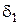=0,02°.

37. Уточняем (по рис.12) коэффициент скорости: φ=0,97.

38. Число Рейнольдса:

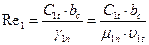
где 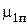=23,5·10^-6кг/м·с – коэффициент динамической вязкости (рис.13 по Р₁=1,116 МПа, t_1t=352,6°C);

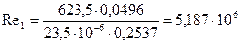. В связи с тем, что 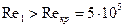, режимы работы решётки находятся в области автомодельности, в которой профильные потери и, следовательно, КПД решётки практически не изменяются.

39. Коэффициент потерь энергии:

.

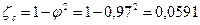40. Абсолютная скорость выхода пара из сопловой решетки:

.

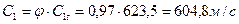41. Относительная скорость на входе в первую рабочую решетку: ,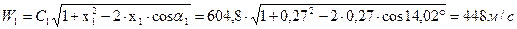

где 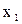=U/C₁=162/604,8=0,27– отношение скоростей.

42. Угол входа потока пара в первую рабочую решетку:

; .

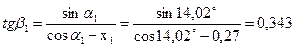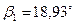43. Потеря энергии в сопловой решетке

Δh_c = ξ_c* 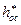= 0,0591∙194,4 = 11,5 кДж/кг.

Параметры пара перед первой рабочей решеткой

h₁ = h_1t + Δh_c = 3161+11,5= 3172,5 кДж/кг,

p₁ =1,116 МПа,

υ₁ = 0,2561м³/кг,

t₁ = 358,1 ⁰С.

Расчет первой рабочей решетки.

44. Теоретическая относительная скорость на выходе из первой рабочей решетки и число Маха:

;

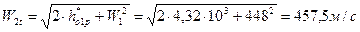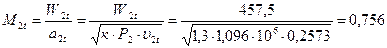
где υ_2t=0,2599 м³/кг (h_2t=3168,2 кДж/кг, t_2t=355,9 °C)по h-s диаграмме точка 2_t (рис.2).

45. Выходная площадь первой рабочей решетки:

;

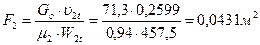где μ₂=0,94 – принятый коэффициент расхода.

46. Выбираем величину перекрыши:

Δl_p=Δl_п+Δl_в=l₂–l₁=4мм;

где Δl_в=2мм – перекрыша у втулки;

Δl_п=2мм – перекрыша на периферии.

47. Считая, что рабочая лопатка первого венца выполняется постоянной по входной и выходной кромкам, получаем: l₂=l₁+Δl_p=63,14+4=67,14 мм.

48. Эффективный угол выхода из первой рабочей решетки:

;

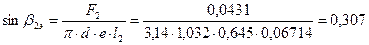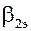=17,89°.

49. По числу Маха и 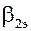выбираем первую рабочую решетку с профилем Р-26-17А и размерами: относительный шаг решетки 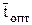= 0,6; хорда табличного значения b_т=2,57 см; В_т=2,5 см; радиус закругления выходной кромки r₂=0,02 см; хорда b_р=51,3 мм; толщина выходной кромки δ_кр=0,8 мм.

50. Число рабочих лопаток первого венца:

.

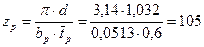51. Относительная толщина выходной кромки профиля:

.

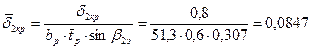52. Угол поворота потока:

Δβ_р=180°-(β₁+β_2э)=180°-(18,93°+17,89°)=143,18°.

53. По отношению b_p/l₂=0,764 и Δβ_р по рис.9 находим коэффициент расхода μ₂=0,942, и уточняем

выходную площадь первой рабочей решетки:

;

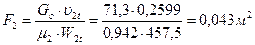эффективный угол выхода из первой рабочей решетки:

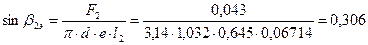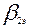; =17,82°.

54. По рис.12 определяем усредненный коэффициент скорости рабочей решетки ψ_р=0,935.

55. Коэффициент потерь энергии:

.

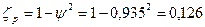56. Число Рейнольдса:

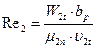
где 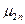=23,5·10^-6кг/м·с–коэффициент динамической вязкости (рис.13 по Р₂=1,096 МПа, t_2t=355,9°C);

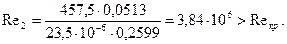Поправка на него не вносится.

57. Действительная относительная скорость выхода пара из рабочей решетки первого венца:

.

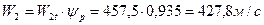58. Окружные и осевые усилия действующие на лопатки первого венца:

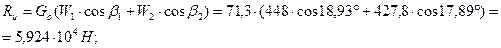
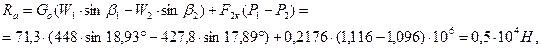
где .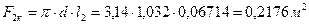

59. Равнодействующая от окружного и осевого усилий:

.

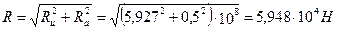60. При постоянном профиле по длине лопатки изгибающее напряжение будет равно:

.

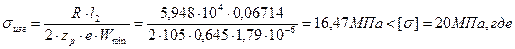
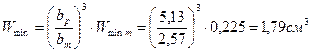61. Потери энергии в первой рабочей решетке:

.

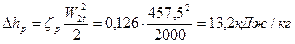62. Состояние пара за первым рабочим венцом ступени.

h₂ = h_2t + Δh_р = 3168,2 + 13,2= 3181,4 кДж/кг,

р₂ = 1,096 МПа,

υ₂ = 0,2626 м³/кг,

t₂ = 362 ⁰C.

63. Абсолютная скорость пара за первой рабочей решеткой:

.

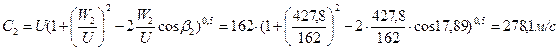64. Угол характеризующий направление С₂:

;

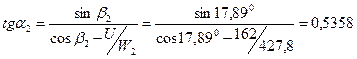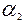=28,18°.

Поворотная решетка

65. Теоретическая скорость выхода пара из поворотной решетки:

.

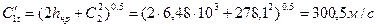66. Число Маха:

,

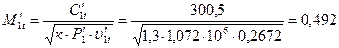где υ_1t’=0,2672 м³/кг (h_1t’=3175 кДж/кг, Р₁’=1,072 МПа) по h-s диаграмме точка 1_t ‘(рис.2).

67. Выходная площадь поворотной решетки:

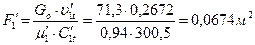
где μ₁’=0,94 –принятый коэффициент расхода.

68. Принимаем перекрышу для поворотной лопатки: Δl_п=4мм.

69. Длина поворотной лопатки: .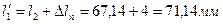

70. Эффективный угол поворотной решетки:

;

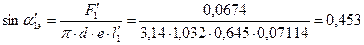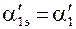=26,94°.

71. Выбираем для поворотной решетки профиль по числу Маха и 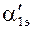выбираем первую рабочую решетку с профилем Р-35-25А и размерами: относительный шаг решетки 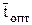=0,55; хорда табличного значения b_m=25,4мм; В_п=2,5см; радиус закругления выходной кромки r₂=0,015см; W_мин=0,168см³; хорда b_п=40,3мм отношением 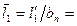71,14/40,3=1,765.

Число рабочих лопаток поворотной решётки:

.

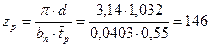72. Относительная толщина выходной кромки профиля поворотной лопатки:

.

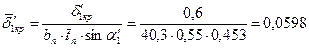73. Угол поворота потока в поворотной решетке:

Δα_п=180°-(α₂+α'_1э)=180°-(28,18°+26,94°)=124,88°.

74. По отношению 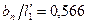и Δα_п по рис.9 находим коэффициент расхода μ'₁=0,956 и уточняем

выходную площадь поворотной решетки:

;

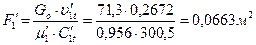эффективный угол поворотной решетки:

;

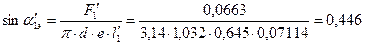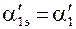=26,49°.

75. По рис.12 определяем усредненный коэффициент скорости поворотной решетки ψ_п=0,94.

76. Коэффициент потерь энергии в поворотной решетке:

.

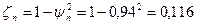77. Число Рейнольдса:

.

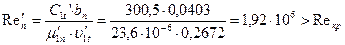78. Потери энергии в поворотной решетке:

.

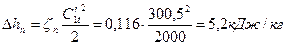79. Состояние пара за поворотной решеткой

h₁^´ = h_1t^´ + Δh_п = 3175+ 5,2 = 3180,2 кДж/кг,

р₁^´ = 1,072 МПа,

υ^´₁ = 0,2683 м³/кг,

t'₁=361,3°C.

80. Действительная скорость выхода пара из поворотной решетки:

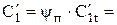0,94·300,5=282,47 м/с.

81. Относительная скорость пара на входе во вторую рабочую решетку: ,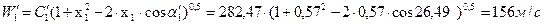

где 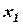=U/C'₁=162/282,47=0,57 – отношение скоростей;

и ее направление: ,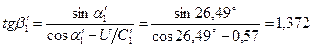

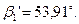
Вторая рабочая решетка

82. Теоретическая относительная скорость на выходе из второй рабочей решетки и число Маха:

;

,

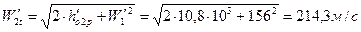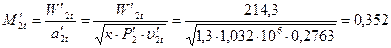где υ'_2t=0,2763 м³/кг (h'_2t=3169,4кДж/кг и Р'₂=1,032 МПа) по h-s диаграмме точка 2'_t (рис.2).

83. Выходная площадь второй рабочей решетки:

;

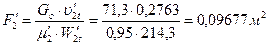где μ'₂=0,95 – принятый коэффициент расхода.

84. Выбираем величину перекрыши:

Δl'_p =4,3мм.

85. Считая, что рабочая лопатка второго венца выполняется постоянной по входной и выходной кромкам, получаем: l'₂=l_п+Δl'_p=71,14+4,3=75,34 мм.

86. Эффективный угол выхода из второй рабочей решетки:

;

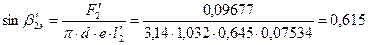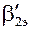=37,95°.

87. По числу Маха и 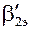выбираем вторую рабочую решетку с профилем Р-60-38А и размерами: относительный шаг решетки 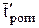=0,5; хорда табличного значения b_т'=2,61см; В_р'=2,5см; радиус закругления выходной кромки r₂=0,02см; W'_мин=0,035 см³; хорда b_р'=60мм и отношение .

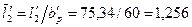Число рабочих лопаток второго венца:

.

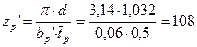88. Относительная толщина выходной кромки профиля поворотной лопатки:

.

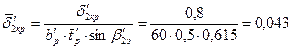89. Угол поворота потока:

Δβ'_2р=180°-(β'₁+β'_2э)=180°-(53,91°+37,95°)=88,14°.

90. По отношению b'_p/l'₂=60/75,34=0,796 и Δβ'_2р по рис.9 находим коэффициент расхода μ'₂=0,96 и уточняем

выходную площадь второй рабочей решетки:

;

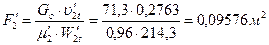эффективный угол выхода из второй рабочей решетки:

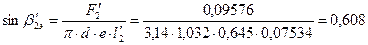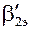; =37,45°.

91. По рис.12 принимаем усредненный коэффициент скорости второй рабочей решетки ψ'_р=0,958.

92. Коэффициент потерь энергии:

.

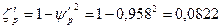93. Число Рейнольдса:

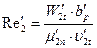
где 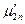=23,5·10^-6кг/м·с – коэффициент динамической вязкости (рис.13 по Р'₂=1,032 МПа, t'_2t=355,8°C);

.

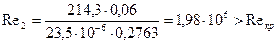94. Потери энергии во второй рабочей решетке:

.

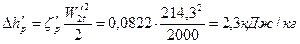95. Параметры пара за регулирующей ступенью

h´₂ = h_2t´ + Δh_р^´= 3169,4+2,3= 3171,7 кДж/кг;

p₂ ´= 1,032 МПа;

υ₂´= 0,2768 м³/кг;

t₂´=356,9 °C.

96. Действительная относительная скорость выхода пара из рабочей решетки второго венца:

.

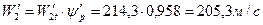97. Окружные и осевые усилия действующие на лопатки первого венца:

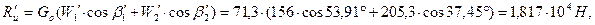
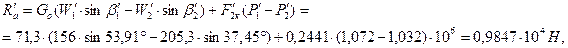
где .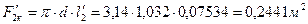

98. Равнодействующая от окружного и осевого усилий:

.

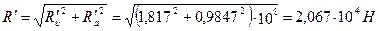99. При постоянном профиле по длине лопатки изгибающее напряжение будет равно:

.

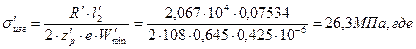
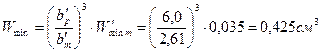100. Абсолютная скорость пара за первой рабочей решеткой:

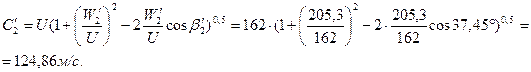
101. Угол характеризующий направление С'₂:

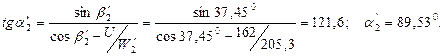
102. Потери энергии с выходной скоростью:

.

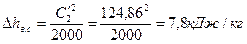103. Относительный лопаточный КПД выраженный через потери:

.

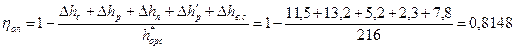104. Относительный лопаточный КПД выраженный через скорости: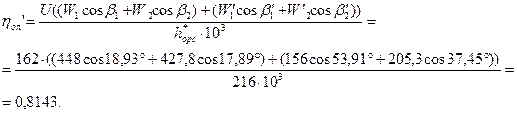

Проверка:

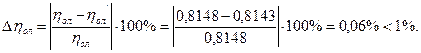
105. Проточная часть рассчитанной регулирующей ступени:

106. Ширина профиля лопатки:

- сопловой:

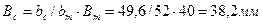
- первой рабочей:

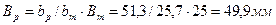
- поворотной:

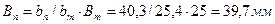
- второй рабочей:

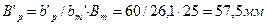
где В_т – ширина табличного профиля.

107. Осевой зазор между направляющими лопатками и рабочими лопатками принимаем равным δ_а=4мм.

108. Радиальный зазор при средней длине лопаток:

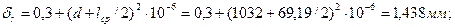
где 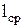=(l₁+l₂+l_п+l'₂)/4=(63,14+67,14+71,14+75,34)/4=69,19 мм.

109. Относительные потери на трение пара в дисках:

а) о торцевые поверхности:

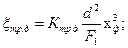
где d – средний диаметр ступени;

F₁ – выходная площадь сопловой решетки;

К_тр.д=f(Re,S/r) – коэффициент трения;

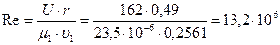
S/r=0,05, принимаем; К_тр.д=0,6·10^-3

б) на трение свободных цилиндрических и конических поверхностей на ободе диска:

;

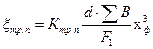где 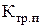=10^-3, принимаем;

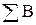=а+в+с=0,022+0,0477+0,022=0,0917 м.

в=2·δ_а+В_п=2·4+39,7=47,7мм;

.

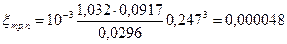в) о поверхности лопаточного бандажа:

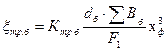
где 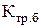=2·10^-3, принимаем;

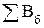=d+e=0,0539+0,0615=0,1154м;

d_б=d+l_cp=1,032 +0,07124=1,103 м;

l_ср=(l₂+l'₂)/2=(67,14+75,34)/2=71,24 мм=0,07124 м

;

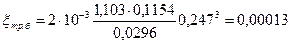общие потери на трение:

.

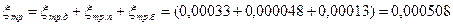110. Потери от парциального подвода пара, складываются из потерь:

- на вентиляцию:

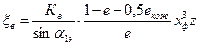
где К_в=0,065 – коэффициент, зависящий от геометрии ступени;

е_кож=0,5 – доля окружности, занимаемая кожухом и устанавливаемого на нерабочей дуге диска для уменьшения вентиляционных потерь при парциальном подводе пара;

z=2 – число венцов ступени скорости;

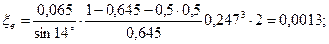
- потери на концах дуг сопловых сегментов (потери на выколачивание)

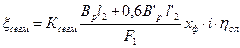
где К_сегм=0,25 – опытный коэффициент;

i=2 – число пар концов сопловых сегментов;

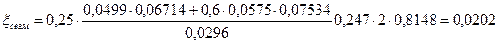
Общие:

.

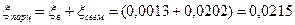111. Относительный внутренний КПД регулирующей ступени выраженный через потери:

η_oi=η_ол – (ζ_тр+ζ_парц)=0,8148 – (0,000508+0,0215)=0,7928.

112. Потери энергии на трение диска:

.

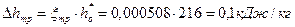113. Потери энергии от парциального впуска пара:

.

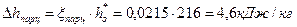114. Откладываем потери Δh_в.с, Δh_тр.д, Δh_парц от точки 2' и получаем точку 2'' с параметрами:

i₂''=i₂'+Δh_в.с+Δh_тр+Δh_парц=3171,1+7,8+0,1+4,6=3184,2 кДж/кг

t''₂=362,8°С, υ''₂=0,2796 м³/кг.

115. Использованный теплоперепад:

.

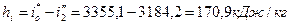116. Внутренняя мощность ступени:

N_i=G_o·h_i=71,3·170,9=12185 кВт.

117. Относительный внутренний КПД выраженный через теплоперепады:

.

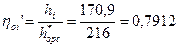Проверка:

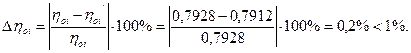
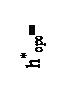
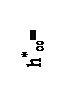
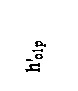
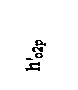
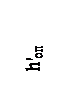
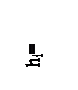
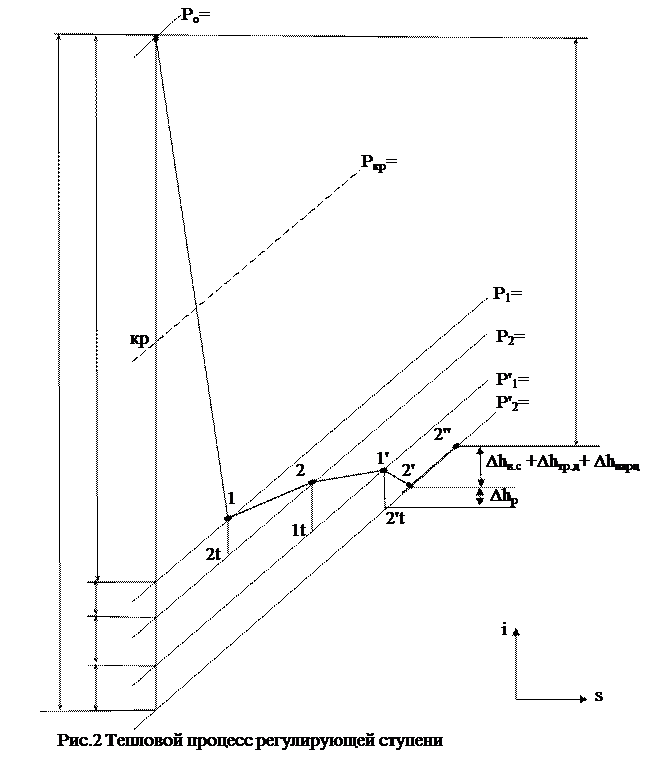
118. Треугольники скоростей двухвенечной регулирующей ступени:

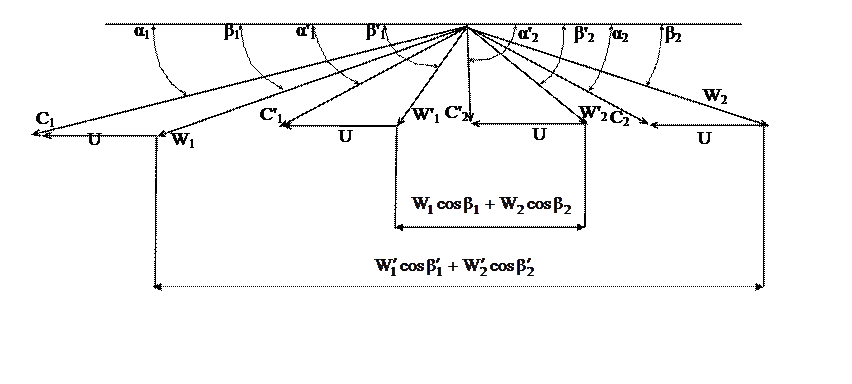
Расчет первой нерегулируемой ступени:

1. Оптимальное отношение скоростей в нерегулируемой ступени:

.

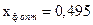2. Принимаем теплоперепад первой регулирующей ступени h_o1нс=50 кДж/кг.

3. Фиктивная скорость в ступени:

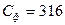м/с.

4. Окружная скорость на среднем диаметре в нерегулируемой ступени:

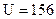м/с.

5. Средний диаметр нерегулируемой ступени:

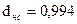м.

8. Теоретическая скорость выхода пара из сопловой решетки:

.

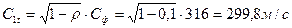9. Располагаемый теплоперепад сопловой решетки:

h_оc=(1 – ρ)h_о1нс=(1 – 0,1)·50=45 кДж/кг.

10. Теоретические параметры пара за сопловой решеткой, точка 1t:

i_1t=i₂''_''–h_ос=3184,2–45=3139,2 кДж/кг, Р₁=0,881 МПа, υ_1t=0,3159 м³/кг, t_1t=340,1 °С.

11. Выходная площадь сопловой решетки:

;

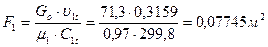где μ₁=0,97 – коэффициент расхода, предварительно принимаем.

12. Длина сопловой лопатки:

.

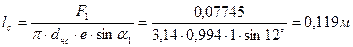13. Число Маха:

.

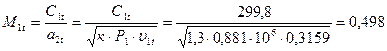14. Оставляя угол α₁=12° и принимая α_о≈90° выбираем сопловую решетку размера С-90-15А со следующими характеристиками: относительный шаг решетки 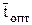=0,76; хорда табличного значения b_т=6,25см; В=3,4см; хорда профиля b_с=49,6мм.

15. Число лопаток:

.

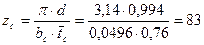16. Относительная толщина выходной кромки:

.

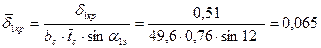17. Относительная длина лопатки:

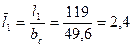; по отношению 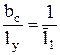=0,42 в соответствии с графиком зависимости μ₁(b_с/l₁) (рис.9), коэффициент μ₁=0,981 уточняем

выходную площадь сопловой решетки:

;

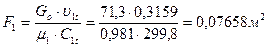длину сопловой лопатки:

.

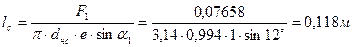18. Число Рейнольдса

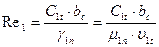
где 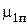=22,4·10^-6кг/м·с–коэффициент динамической вязкости (рис.13 по Р₁=0,881 МПа, t_1t=340,1°C);

.

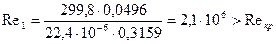19. Коэффициент скорости φ=0,974 (рис.12).

20. Коэффициент потерь энергии:

.

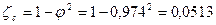21. Абсолютная скорость выхода пара из сопловой решетки:

.

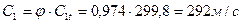22. Относительная скорость на входе в первую рабочую решетку: ;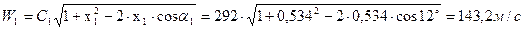

где 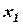=U/C₁=156/292=0,534 – отношение скоростей.

23. Угол входа потока пара в первую рабочую решетку:

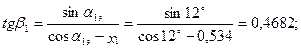β₁ = 25,09 ⁰.

24. Потери энергии в сопловой решетке:

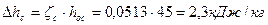; откладываем эти потери в i-s диаграмме и получаем точку 1, (рис.3), характеризующую действительное состояние пара перед первой рабочей решеткой имеющей следующие параметры: Р₁=0,881 МПа; i₁=3141,5 кДж/кг; υ₁=03165 м³/кг; t₁=341,2 °С.

25. Располагаемый теплоперепад рабочей решетки:

h_op=ρ·h_о1нс=0,1·50=5 кДж/кг, откладываем его из точки 1 и получаем точку 2_t с параметрами i_2t=3136,5 кДж/кг, Р₂=0,866 МПа; υ_2t=0,3207 м³/кг; t_2t=338,7 °С.

26. Теоретическая относительная скорость на выходе из рабочей решетки и число Маха:

;

.

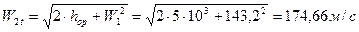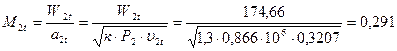27. Выходная площадь рабочей решетки:

;

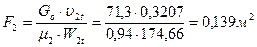где μ₁=0,94 – коэффициент расхода, предварительно принимаем.

28. Принимаем перекрышу Δl_р=l₂ – l₁=3,5 мм.

29. Длина рабочей лопатки l₂= l₁+ Δl_р=118+3,5=121,5 мм.

30. Эффективный угол выхода из рабочей решетки:

;

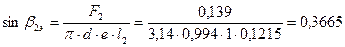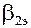=21,5°.

31. По числу Маха и 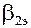выбираем вторую рабочую решетку с профилем Р-30-21А и размерами: относительный шаг решетки 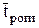=0,61; хорда табличного значения b_т=2,56см; В=2,5см; хорда b_р=30,9мм.

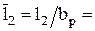121,5/30,9=3,932.

32. Число лопаток:

.

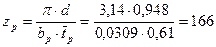33. Относительная толщина выходной кромки:

.

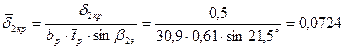34. Угол поворота потока:

Δβ_2р=180°-(β₁+β_2э)=180°-(25,09°+21,5°)=133,41°.

35. По отношению 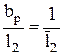=0,254 и Δβ_р по рис.9 находим коэффициент расхода μ₂=0,952 и уточняем

выходную площадь рабочей решетки:

;

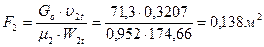эффективный угол выхода из рабочей решетки:

;

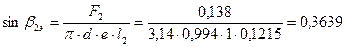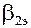=21,34°.

36. Число Рейнольдса

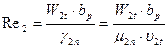
где 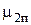=22,4·10^-6 кг/м·с–коэффициент динамической вязкости (рис.13 по

Р₂=0,866 МПа, t_2t=338,7°C);

.

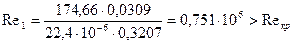37. Коэффициент скорости ψ=0,942 (рис.12).

38. Коэффициент потерь энергии:

.

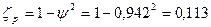39. Относительная скорость пара за рабочей решеткой:

W₂=ψ·W_2t=0,942·174,66=164,53 м/с.

40 Абсолютная скорость пара за рабочей решеткой:

.

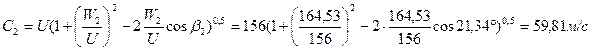41. Угол характеризующий направление С₂:

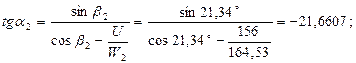
α₂ =-87,36º.

42. Окружное и осевое усилие и их равнодействующая:

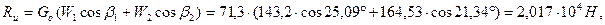
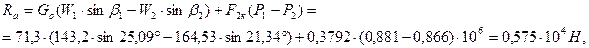
где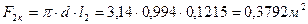

.

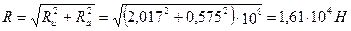43. Момент сопротивления при постоянном профиле по длине лопатки:

.

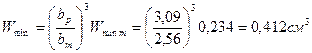44. Изгибающее напряжение:

.

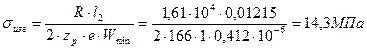45. Потери энергии в рабочей решетке:

.

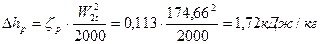46. Потери энергии с выходной скоростью:

.

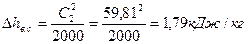47. Относительный лопаточный КПД выраженный через потери:

.

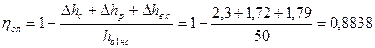48. Относительный лопаточный КПД выраженный через скорости:

.

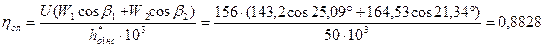Проверка:

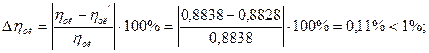
49. Число Рейнольдса:

.

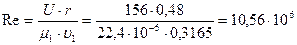50. Принимаем S/r=0,05.

51. Потери на трение в дисках:

- коэффициент потерь

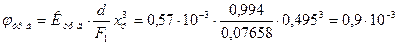
где К_тр.д – определяется по рис.17

- потери энергии:

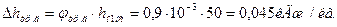
51. Относительный внутренний КПД выраженный через потери:

.

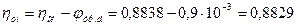52. Откладываем на рис.3 потери Δh_р,_. получаем т.2 с параметрами:

i₂=i_2t+Δh_р=3136.5+1,72=3138,2 кДж/кг, Р₂=0,866 МПа; υ₂=0,3211 м³/кг; t'₂=339,5°С.

Откладываем на рис.3 потери Δh_р,Δh_тр.д,Δh_в.с получаем т.2' с параметрами:

i'₂=i_2t+ Δh_р+Δh_тр.д+Δh_в.с=3136.5+1,72+0,045+1,79=3140 кДж/кг, Р₂=0,871 МПа; υ'₂=0,3197 м³/кг; t'₂=340,4°С.

53. Использованный теплоперепад:

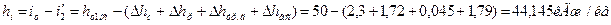
54. Относительный внутренний КПД выраженный через теплоперепады:

.

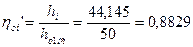Проверка:

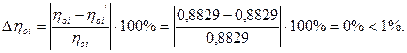
55. Внутренняя мощность ступени:

.

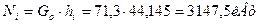Расчет второй нерегулируемой ступени:

1. Располагаемый теплоперепад второй нерегулируемой ступени между изобарами Р₂=0,866 МПа и Р_z=0,71 МПа по изоэнтропе 2 – z'_t(рис.3):

h_о2нс=i₂-i_zt'=3138,2–3084 =54,2 кДж/кг.

2. Располагаемый теплоперепад по заторможенным параметрам с учетом использования кинетической энергии от выходной скорости из предыдущей ступени:

.

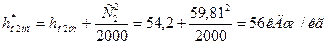3. Средний диаметр ступени принимаем: d₁= d₂=0,994 м.

4. Окружная скорость: U₁= U₂=156м/с.

5. Фиктивная скорость в ступени:

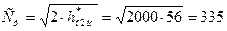м/с.

6. Отношение скоростей в нерегулируемой ступени:

.

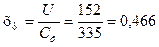7. Угол выхода потока пара из сопловой решетки принимаем 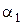=12°.

8. Степень реактивности ступени принимаем ρ=0,1.

9. Теоретическая скорость выхода пара из сопловой решетки:

.

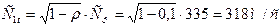10. Располагаемый теплоперепад сопловой решетки:

h^*_оc=(1– ρ)h^*_о2нс=(1– 0,1)·56=50,4 кДж/кг.

11. Теоретические параметры пара за сопловой решеткой, точка 1t:

i_1t=i^/_2'–h^*_оc=3140–50,4=3089,6кДж/кг,

Р₁=0,724МПа, υ_1t=0,3688м³/кг, t_1t=314,9°С.

12. Выходная площадь сопловой решетки:

,

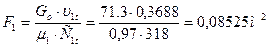где μ₁=0,97 – коэффициент расхода, предварительно принимаем.

13. Длина сопловой лопатки:

.

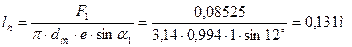14. Число Маха:

.

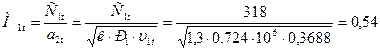15. Оставляя угол α₁=12° и принимая α_о≈90° выбираем сопловую решетку С-90-12А со следующими характеристиками: относительный шаг решетки 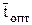=0,76; хорда табличного значения b_т=6,25см; В=3,4см; хорда профиля b_с=49,6мм.

16. Число лопаток:

.

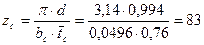17. Относительная толщина выходной кромки:

.

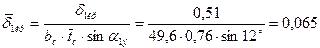18. Относительная длина лопатки:

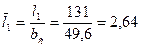; по отношению 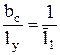=0,379 в соответствии с графиком зависимости μ₁(b_с/l₁) (рис.9), коэффициент μ₁=0,982 уточняем

выходную площадь сопловой решетки:

;

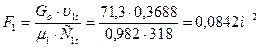длину сопловой лопатки:

.

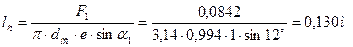21. Число Рейнольдса

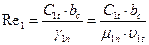
где 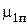=21,2·10^-6кг/м·с–коэффициент динамической вязкости (рис.13 по Р₁=0,724 МПа, t_1t=314,9 °C);

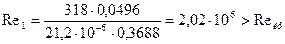
22. Коэффициент скорости φ=0,975 (рис.12).

23. Коэффициент потерь энергии:

.

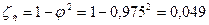24. Абсолютная скорость выхода пара из сопловой решетки:

.

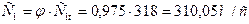25. Относительная скорость на входе в первую рабочую решетку: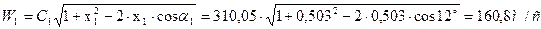

где 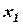=U/C₁=156/310,05=0,503 – отношение скоростей.

26. Угол входа потока пара в первую рабочую решетку:

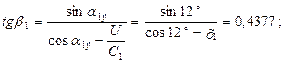β₁ = 23,64 ⁰.

27. Потери энергии в сопловой решетке:

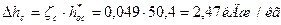; откладываем эти потери в i-s диаграмме и получаем точку 1,(рис.3), характеризующую действительное состояние пара перед первой рабочей решеткой имеющей следующие параметры:

Р₁=0,724 МПа; i₁=3092,1 кДж/кг; υ₁=0,3696 м³/кг; t₁=316,1 °С.

28. Располагаемый теплоперепад рабочей решетки: откладываем адиабату из точки 1 до давления Р_z=Р₂=0,71 МПа и получаем точку 2t с параметрами i_zt''=308 кДж/кг, υ_zt''=0,3752 м³/кг; t_zt''=313,4 °С; .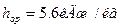

29. Теоретическая относительная скорость на выходе из рабочей решетки и число Маха:

;

.

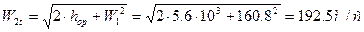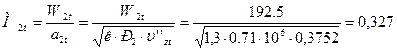30. Выходная площадь рабочей решетки:

,

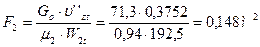где μ₂=0,94 – коэффициент расхода, предварительно принимаем.

31. Принимаем перекрышу Δl_р=l₂ – l₁=3,8 мм.

32. Длина рабочей лопатки l₂= l₁+ Δl_р=130+3,8=133,8 мм.

33. Эффективный угол выхода из рабочей решетки:

;

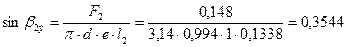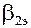=20,76°.

34. По числу Маха и 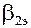выбираем вторую рабочую решетку с профилем Р-30-21А и размерами: относительный шаг решетки 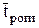=0,61; хорда табличного значения b_т=2,56см; В=2,5см; хорда b_р=40мм;, 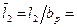4,33.

35. Число лопаток:

.

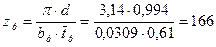36. Относительная толщина выходной кромки:

.

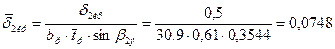37. Угол поворота потока:

Δβ_2р=180°-(β₁+β_2э)=180°-(23,64°+20,76°)=135,6°.

38. По отношению 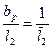=0,231 и Δβ_р по рис.9 находим коэффициент расхода μ₂=0,952 и уточняем выходную площадь рабочей решетки:

;

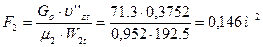эффективный угол выхода из рабочей решетки:

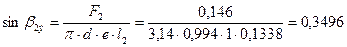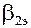; =20,46°.

39. Число Рейнольдса

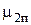=21,1·10^-6 кг/м·с–коэффициент динамической вязкости (рис.13 по Р₂=0,71 МПа, t''_zt=313,4 °C);

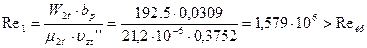; режим работы решетки в автомодельной зоне и поправка на Re не вносится.

40. Коэффициент скорости ψ=0,942 (рис.12).

41. Коэффициент потерь энергии:

.

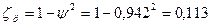42. Относительная скорость пара за рабочей решеткой:

W₂=ψ·W_2t=0,942·192,5=181,34 м/с.

43. Абсолютная скорость пара за рабочей решеткой:

Дата добавления: 2015-07-20