
Читайте также:
|
Задача 1. Пластина D ограничена линиями: y = 4 – x 2; х = 0; y = 0 (x ≥ 0; y ≥ 0) Поверхностная плотность γ 0 = 3.
Решение. Область, заданная в задаче, ограничена параболой y = 4 – x 2, осями координат и лежит в первой четверти (рис. 1). Задачу будем решать в декартовой системе координат. Эта область может быть описана системой неравенств:
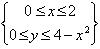
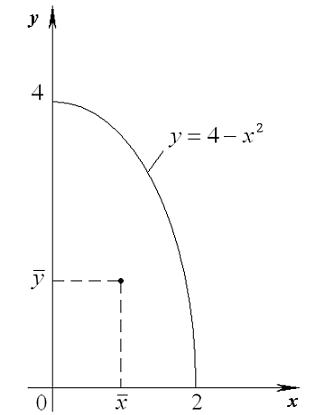
Рис. 1
Площадь S пластины равна (1):
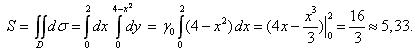
Так как пластина однородная, ее масса m = γ 0 S = 3· 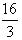 = 16.
= 16.
По формулам (3), (4) найдем статические моменты пластины:
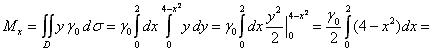
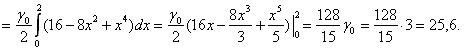
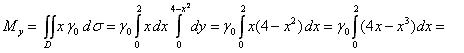
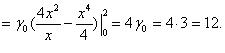
Координаты центра масс находятся по формуле (6):
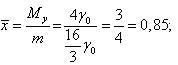
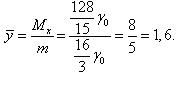
Ответ: S ≈ 5,33; m = 16; Mx = 25,6; My = 12;  = 0,75;
= 0,75; 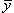 = 1,6.
= 1,6.
Задача 2. Пластина D ограничена линиями: х 2 + у 2 = 4; х = 0, у = х (х ≥ 0, у ≥ 0). Поверхностная плотность γ (x,y) = у.
Решение. Пластина ограничена окружностью и прямыми, проходящими через начало координат (рис. 2). Поэтому для решения задачи удобно использовать полярную систему координат. Полярный угол φ меняется от π/4 до π/2. Луч, проведенный из полюса через пластину, «входит» в неё при ρ = 0 и «выходит» на окружность, уравнение которой: х 2 + у 2 = 4 <=> ρ = 2.
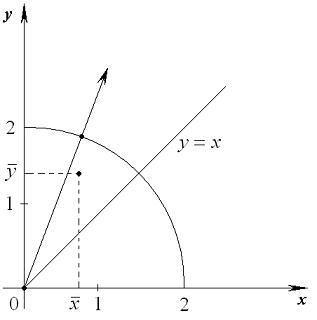
Рис. 2
Следовательно, заданную область можно записать системой неравенств:
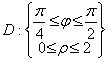
Площадь пластины найдем по формуле (1):
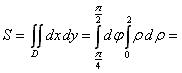
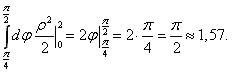
Массу пластины найдем по формуле (2), подставив γ (x,y) = у = ρ sin φ:

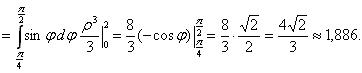
Для вычисления статических моментов пластины используем формулы (3) и (4):
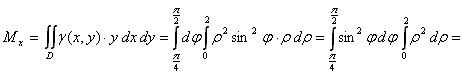
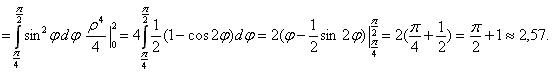
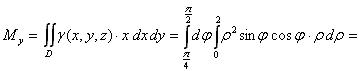

Координаты центра масс получим по формулам (6):

Ответ: S ≈ 1,57; m ≈ 1,886; Mx = 2,57; My = 1;  = 0,53;
= 0,53; 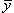 = 1,36.
= 1,36.
Дата добавления: 2015-07-20; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Порядок выполнения типового расчета | | | ПРОВОЗГЛАШЕНИЯ #1 |