Розв'язування систем лінійних рівнянь методом Гаусса

При розв'язуванні систем лінійних рівнянь користуються також ме­тодом послідовного виключення невідомих або методом Гаусса. Він по­лягає ось у чому: систему рівнянь зводять до рівносильної системи з трикутною матрицею (матриця, в якій усі елементи, що розміщені нижче головної діагоналі, дорівнюють нулю). Такі дії називають прямим ходом. З отриманої трикутної системи невідомі змінні визначають за допомогою послідовних підстановок (зворотний хід).

Для виконання прямого ходу здійснюють такі перетворення:

1) множать або ділять коефіцієнти і вільні члени на одне й те саме число;

2) додають і віднімають рівняння;

3) переставляють рівняння системи;

4) виключають із системи рівняння, в яких усі коефіцієнти при неві­домих та вільні члени дорівнюють нулю.

За допомогою операцій 1) і 2) можна виключити будь-яке невідоме з усіх рівнянь системи, крім одного. При цьому невідоме, яке виключають, називають провідним невідомим, а рівняння, в якому зберігаються про­відне невідоме, - провідним.

Приклад 1. Розв'язати методом Гаусса систему лінійних рівнянь

За провідне рівняння виберемо друге рівняння, а за провідне неві­доме виберемо . Переставимо друге рівняння на місце першого:

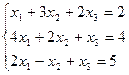
Запишемо матрицю, яка складається з коефіцієнтів системи і стовпця вільних членів. Таку матрицю називають розширеною матрицею системи. Стовпець вільних членів відокремлюємо від матриці коефіцієнтів

системи вертикальною рискою:

Для того щоб у першому стовпці дістати а₂₁ = a₃₁, =0. помножимо перший рядок спочатку на -4 і додамо до другого рядка, а потім на -2 і додамо до третього рядка:

Поділимо другий рядок на -10, отримані результати помножимо на 7 і додамо до третього рядка:

Запишемо нову рівносильну систему, яка відповідає отриманій розширеній матриці

Виконуючи зворотний хід, за допомогою послідовних підстановок знаходимо

Отже, дістали відповідь: (1;-1;2).

Приклад 2. Розв'язати методом Гаусса систему лінійних рівнянь

Складемо розширену матрицю системи

.

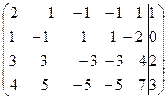Поміняємо місцями перше і друге рівняння системи та виключимо з другого, третього і четвертого рівнянь. Дістанемо

.

Послідовно помножимо другий рядок на 2 і 3 і отримані результати відповідно віднімемо з третього та четвертого:

.

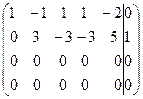Відкинувши нульові рядки, дістанемо матрицю

Ця розширена матриця відповідає системі рівнянь

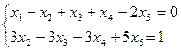
Звідки

Дана система має безліч розв'язків. Тут змінні і подано через змінні 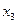, , .Такий розв'язок системи називають загальним розв'язком, змінні , називаються базисними, змінні 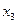, , - вільними. Надаючи вільним змінним будь-які фіксовані значення, діс­таватимемо частинні розв'язки. Нехай 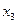= = =0. Тоді , . Отже, маємо частинний розв'язок вигляду , який називають базисним розв'язком.

Запитання і завдання

1. Як розв’язуються системи лінійних рівнянь за формулами Крамера.

2. Як розв’язуються системи лінійних рівнянь методом Гаусса.

3. Як розв'язуються системи лінійних рівнянь методом оберненої матриці.

4. Розв’яжіть системи рівнянь:

а) , б)

5. Двоє робітників, працюючи одночасно, виконують всю роботу за 5 днів. Якби перший працював удвоє швидше, а другий – удвоє повільніше, то вони виконали б усю роботу за 4 дні. За скільки днів виконав би всю роботу кожний робітник, працюючи самостійно, якщо продуктивність праці у них однакова?

Дата добавления: 2015-07-20