Розв'язування систем лінійних рівнянь за формулами Крамера

Тема: Загальна теорія систем лінійних рівнянь.

План

1. Розв'язування систем лінійних рівнянь за формулами Крамера.

2. Розв'язування систем лінійних рівнянь методом Гаусса.

3. Розв'язування систем лінійних рівнянь методом оберненої матриці.

4. Приклади.

Ключові поняття і терміни:

- системи лінійних рівнянь,

- метод Гауса,

- метод Крамера.

Література:

1. Грисенко М.В., Математика для економістів.-К.: «Либідь»,- 2007р.,

стор. 7-44.

2. Рудавський Ю.К., Костробій П.П., Д.В.Уханська, Лінійна алгебра та аналітична геометрія.-Л.: «Бескід Біт»,-2002р., стор.7-54.

3. Овчинников П.П., Яремчук Ф.П., Михайленко В.М., Вища математика, ч.1.,-К.: «Техніка»,-2003р., стор. 23-34.

4. Лейфура В.М., Голодницький Г.І., Файст Й.І., Математика.-К.: «Техніка», -2003р., стор. 264-298.

5. Пономаренко О.І., Перестюк М.О., Бурим В.М., Основи математичної економіки.-К.: «Інформ техніка», -1995р.

Розв'язування систем лінійних рівнянь за формулами Крамера

Розглянемо систему лінійних рівнянь з двома невідомими

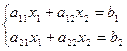(1)

Нехай 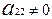. Тоді система (1) рівносильна системі

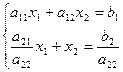(2)

Друге рівняння системи (2) помножимо на д_|2 і віднімемо почленно від першого рівняння. Дістанемо

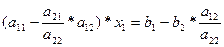(3)

Якщо 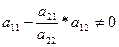, тобто 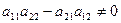,то

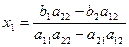. (4)

Підставивши це значення x₁ у друге рівняння системи (2), дістанемо

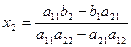. (5)

Неважко помітити, що формули (4) і (5) можна записати за допомогою визначників другого порядку:

, ,

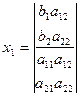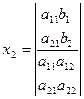Або

, ,

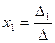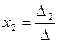Де

, , .

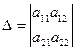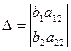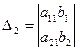Зауважимо, що визначник 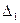, дістаємо з визначника 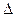заміною пер­шого стовпця стовпцем вільних членів, а визначник 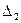- з визначника 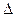заміною другого стовпця стовпцем вільних членів.

Метод визначників можна застосовувати до систем і з будь-якою кіль­кістю рівнянь(і відповідною кількістю невідомих).

Дата добавления: 2015-07-20