Алгоритм Форда-Беллмана нахождения минимального пути

ЛАБОРАТОРНАЯ РАБОТА №10

Предполагается, что ориентированный граф не содержит контуров отрицательной длины.

Алгоритм Форда-Беллмана

Основными вычисляемыми величинами этого алгоритма являются величины λ_j(k), где i = 1, 2, …, n (n – число вершин графа); k = 1, 2, …, n – 1. Для фиксированных i и k величина λ_j(k) равна длине минимального пути, ведущего из заданной начальной вершины х₁ в вершину х_i и содержащего не более k дуг.

Шаг 1. Установка начальных условий.

Ввести число вершин графа n и матрицу весов C = (c_ij).

Шаг 2. Положить k = 0. Положить λ_i(0) = ∞ для всех вершин, кроме х₁; положить λ_i(0) = 0.

Шаг 3. В цикле по k, k = 1,..., n – 1, каждой вершине x_i на k-ом шаге приписать индекс λ_i(k) по следующему правилу:

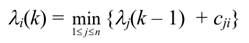(6.1)

для всех вершин, кроме х₁, положить λi(k) = 0.

В результате работы алгоритма формируется таблица индексов λi(k), i = 1, 2, …, n, k = 0, 1, 2, …, n – 1. При этом λ_i(k) определяет длину минимального пути из первой вершины в i -ую, содержащего не более k дуг.

Шаг 4. Восстановление минимального пути.

Для любой вершины x_s предшествующая ей вершина x_r определяется из соотношения:

(6.2)

где G ^-1(x_s) - прообраз вершины x_s.

Для найденной вершины xr предшествующая ей вершина xq определяется из соотношения:

,

где G ^-1(x_r) - прообраз вершины x_r, и т. д.

Последовательно применяя это соотношение, начиная от последней вершины xi, найдем минимальный путь.

Дата добавления: 2015-07-20