Замена переменных в двойном интеграле (общий случай).

Рассмотрим двойной интеграл 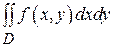в декартовых прямоугольных координатах (х, у). Предположим, что переменные х и у являются функциями независимых переменных u и v, т.е. . Если эти функции непрерывно дифференцируемы и осуществляют взаимно-однозначное отображение ограниченной и замкнутой области D плоскости Оху на область Ω плоскости Оuv и якобиан

, то справедлива формула замены переменной в двойном интеграле:

(4)

Координаты (u, v) называются криволинейными координатами точки (х, у). Цель замены переменных – упрощение вычисления двойного интеграла.

Замечание: Если замена осуществляется функциями , то величина

.

Решение типовых примеров:

Пример 1. Вычислить двойной интеграл , если область D – параллелограмм со сторонами у =2 х -3, у =2 х +5, у =- х +7, у =- х -1.

Решение: Параллелограмм изображен на рис.14а. Хотя подъинтегральная функция и область интегрирования простые, вычисление данного интеграла в прямоугольных координатах Оху приводит к громоздким вычислениям.

Заметим, что уравнения прямых можно записать в виде: у -2 х =3, у -2 х =5, у + х =7, у + х =1. Перейдем к новым координатам с помощью замены , откуда находим . Вычисляем и получаем .

В новой системе координат Ouv область Ω ограничена прямыми u =3, u =5, v =-1, v =7, т.е. представляет собой прямоугольник (рис.17б), а подъинтегральная функция равна . Переходим к вычислению интеграла:

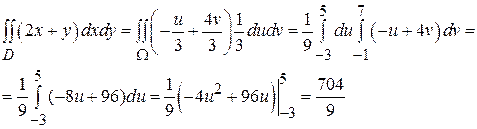
Пример 2. Вычислить , где D ограничена кривыми 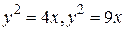, ху =1, ху =5.

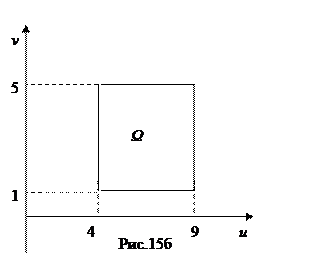
Решение: Область D изображена на рис.15а. Из рисунка видно, что расставить пределы интегрирования для данной области не очень просто, однако подходящая замена переменных позволяет свести этот интеграл к интегралу по прямоугольной области. Нетрудно увидеть, что на границе области D величины и ху являются постоянными. Поэтому введем новые переменные

и вычислим . Отсюда находим . Граница области Ω на плоскости Ouv описывается прямыми u =4, u =9, v =-1, v =5 (рис.15б), поэтому в новых переменных двойной интеграл вычисляется много проще:

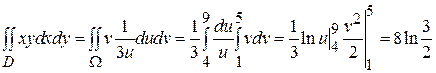
Пример 3. Вычислить 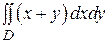, если D ограничена параболой и прямыми х + у =4 и х + у =12.

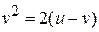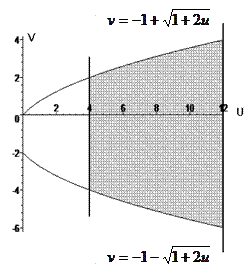
Решение: Область D приведена на рис.16а. Для упрощения области интегрирования введем следующую замену переменных , откуда выражаем х = u - v и подставляем в уравнение параболы . Разрешая квадратное уравнение , получаем уравнение образа исходной параболы на плоскости Ouv: 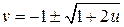. Область Ω ограничена параболой, определенной при , вершина которой находится в точке и прямыми u =4, u =12 (рис.16б). Вычисляем якобиан и применяем формулу замены переменной в двойном интеграле:

Рис.16а Рис.16б

Дата добавления: 2015-07-20