Расчет прогиба плиты

Расчет изгибаемых элементов по прогибам производят из условия

f ≤ fult,

(2.7)

где f - прогиб элемента от действия внешней нагрузки;

f_ult - значение предельно допустимого прогиба.

Прогиб плиты ограничивается эстетическими требованиями.

Для элементов постоянного сечения, работающих как свободно опертые или консольные балки, прогиб допускается определять, вычисляя кривизну только для наиболее напряженного сечения и принимая для остальных сечений кривизны изменяющимися пропорционально значениям изгибающего момента, т.е. по формуле

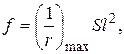
(2.8)

где - полная кривизна в сечении с наибольшим изгибающим моментом;

S - коэффициент, принимаемый по прил.14.

Полную кривизну изгибаемых элементов определяют:

а) для участков без трещин в растянутой зоне по формуле

(2.9)

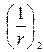где и - кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок;

- кривизна от непродолжительного действия усилия предварительного обжатия Р (т.е. при действии M = Pe_op).

Кривизну элемента на участке без трещин определяют по формуле

(2.10)

где М - изгибающий момент от внешней нагрузки или момент усилия предварительного обжатия относительно оси, проходящей через центр тяжести приведенного сечения;

I_red - момент инерции приведенного сечения относительно его центра тяжести, определяемый как для сплошного тела по общим правилам сопротивления упругих материалов с учетом всей площади бетона и площадей сечения арматуры с коэффициентом приведения арматуры к бетону, равным а=E_s /E_{b 1}; E_{b 1}- модуль деформации сжатого бетона, принимаемый равным:

- при непродолжительном действии нагрузки

Eb 1= 0,85 Eb;

(2.11)

- при продолжительном действии нагрузки

(2.12)

б) для участков с трещинами в растянутой зоне по формуле

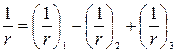
(2.13)

где - кривизна от непродолжительного действия всех нагрузок, на которые производят расчет по деформациям;

- кривизна от непродолжительного действия постоянных и длительных нагрузок;

- кривизна от продолжительного действия постоянных и длительных нагрузок.

Кроме того, в формулах (2.9) и (2.13) может быть учтена кривизна , обусловленная остаточным выгибом элемента вследствие усадки и ползучести бетона в стадии изготовления от усилия предварительного обжатия Р ₍₁₎и собственного веса элемента. Значение определяется по формуле

(2.14)

где σ_sb и σ'_sb - значения, численно равные сумме потерь предварительного напряжения арматуры от усадки и ползучести бетона соответственно для арматуры растянутой зоны и для арматуры, условно расположенной на уровне крайнего сжатого волокна бетона.

Для сечений при h'_f ≤ 0,3 h_o и a'_s < 0,2 h ₀ кривизну допускается определять по формуле

(2.15)

где φ_с - коэффициент, определяемый по прил. 13 в зависимости от φ_f, μa_{s 2}, e_s / h ₀

Пример расчета. Определяем кривизну в середине пролета от продолжительного действия постоянных и длительных нагрузок, т.е. при М = M_l = 107,05 кН·м.

Для этих нагрузок имеем: , φ_f = 0,95,

При продолжительном действии нагрузки и нормальной влажности имеем ε_{b 1, red} =28×10^-4 при влажности окружающей среды 70 ≥W ≥ 40 %.

Тогда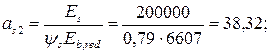

По табл. П13 приложения при φ_f = 0,95, e_s/h ₀ =1,35 и μα_{s 2} =0,36 находим φ_c =0,61. Тогда кривизна равна

Определим кривизну, обусловленную остаточным выгибом при σ_sb =125,16 МПа.

_1/мм

σ_sb – численно равны сумме потерь напряжений от усадки и ползучести бетона σ_sb = 40+85,16=125,16 МПа.

Полная кривизна в середине пролета от постоянных и длительных нагрузок равна

Прогиб плиты определяем, принимая S =5/48:

Согласно СП 20.13330.2011 «Нагрузки и воздействия» поз.2 при l = 5,84 м предельно допустимый из эстетических требований прогиб равен f_ult = 5840 / 200 =29,2 мм, что превышает вычисленное значение прогиба.

Дата добавления: 2015-07-20