Обработка результатов

Потери удельной анергии жидкости на рассматриваемом участке могут быть определены из уравнения Д. Бернулли (11) как разность полных, удельных энергий в сечениях, ограничивающих этот участок:

Поскольку замеры выполняются не прямолинейном горизонтальном участке (рис.10) трубы постоянного диаметра, второе и третье слагаемые в правой части уравнения (20) равны нулю.

Потери энергии на участке являются только потерями по длине трубы, так как участок не содержит каких-либо местных сопротивлений. Таким образом:

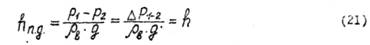
Следовательно, перепад h, фиксируемый дифференциальным манометром 12, представляет собою величину потерь на трение по длине трубы: h=h_{пд .}.

Для определения коэффициента потерь на трение используют формулу Дарси-Вейсбаха:

где λ - коэффициент потерь на трение;

l - длина рассматривавемого участка трубопровода, м;

d - диаметр трубопровода, м;

V_ср - средняя скорость движения жидкости в трубопроводе, м/с.

По формуле (22) определяют значение коэффициента λ:

При заданных значениях d=0,08м; l=4,2м и g=9,81м/с².

Среднюю скорость в трубопроводе на рассматриваемом участке определяют при помощи уравнения неразрывности, а расход – по показаниям водяного дифференциального манометра 3, подключенного к расходомерной шайбе 2 (см. формулы (15) и (16) к лабораторной работе 2). Площадь поперечного сечения трубопровода ω=0.005м². Кинематический коэффициент вязкости ν_t находят по графику ν_t =f(t°C) (см. рис. 17) в зависимости от температуры воды в трубопроводе которую замеряют во время проведения опыта.

Для каждого режима вычисляют значения коэффициентов потерь на трение λ и числа Рейнольдса и строят график λ=f(Re) (рис.18).

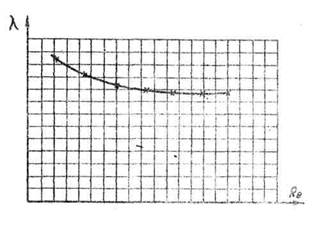
Рисунок 18 – График зависимости λ=f(Re)

Опытные значения λ сравнивают со значениями, получаемыми при использовании эмпирических зависимостей. Многочисленные исследования сопротивления движению жидкости в трубопроводах позволили выделить четыре основные области сопротивления.

Область 1 – вязкого сопротивления; движение ламинарное; Re<2320; λ=f(Re). Коэффициент λ определяют по формуле Пуазейля:

Область 2 – гидравлически гладких труб; режим турбулентный;

2320≤ Re≤20·d/D _э; λ=f(Re).

Для определения λ в пределах этой зоны пользуются формулами:

формулой Блазиуса при 4000≤ Re≤10⁵:

формулой Кольбрука при 2320≤ Re≤3∙10⁶:

Область 3 – доквадратичного сопротивления, переходная от зоны гидравлически гладких труб к зоне квадратичного сопротивления; режим турбулентный; λ=f(Re, D _э /d), где D _э – абсолютная величина эквивалентной равномерно-зернистой шероховатости, численное значение которой в данной работа следует принимать равным D_э = 1.0 мм (для старых заржавленных труб); 20·d/D _э ≤ Re≤500∙d/D _э;

Для определения λ в этой зоне наиболее универсальной является формула Альтшуля:

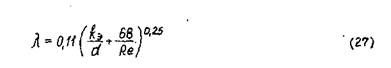
Область 4 – квадратичного сопротивления (автомодельности);

режим турбулентный; λ=f(D_э/d); Re>500∙d/D_э. Коэффициент λ определяют по формуле Шифринсона:

(28)

Результаты всех расчетов заносят в протокол.

Протокол испытаний

d=80мм	Dэ=1мм
l=4,2м	d/Dэ=80.0
t°C=	ω=0,005м^2
νt=

№ п./п замеров	Опытные данные	Расчетные значения λ по формулам
h мм.вод. ст.	Q ма/с	Vср м/с	h п.д. м. вод. ст.		Re	(24)	(25)	(26)	(27)	(28)

Содержание отчета

1. Вычертить схему установки.

2. Записать основные расчетные формулы.

3. Оформить протокол испытаний.

4. Построить опытный график λ=f(Re).

Вопросы для самоконтроля

1. Причины, вызывающие потери энергии на трение.

2. Зоны сопротивления и качественная зависимость коэффициента λ в каждом из них. Объясните эту зависимость с физической точки зрения.

3. Как определяют потери энергии на трение?

4. Запишите формулы Дарси, Пуазейля и Блазиуса.

5. Как зависят потери напора от расхода воды в трубе?

Дата добавления: 2015-07-20