Условия устойчивости линейных систем.

Устойчивостью называют способность системы восстанавливать состояние равновесия, из которого она была выведена в результате какого-либо воздействия.

Устойчивость является одним из основных показателей АСР, определяющих ее работоспособность. Поэтому при исследовании системы необходимо проводить анализ ее устойчивости. Автоматическая система будет устойчивой, если ее выходная величина остается ограниченной при любых ограниченных по абсолютной величине входных воздействий. Система будет неустойчивой, если при сколь угодно малых отклонениях от состояния равновесия она не возвращается к нему, а совершает около него недопустимо большие колебания или непрерывно удаляется от него. Такие системы неработоспособны.

Поведение автоматической системы регулирования при наличии в ней возмущающих и управляющих воздействий описывается дифференциальным уравнением

(1)

где a_0t а₁,..., а_п и b₀, b₁..., b_m – постоянные коэффициенты. Процесс регулирования определяется решением этого дифференциального уравнения (1), представляющего собой сумму частного решения неоднородного уравнения (1) с правой частью и общего решения уравнения (20) без правой части, т. е.

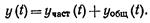
Первое слагаемое этого уравнения называется вынужденным решением (в случае y_част(0)=const это будет установившееся значение), а второе слагаемое–переходной составляющей.

Система будет устойчивой, если с течением времени при переходная составляющая будет стремиться к нулю. Найдем эту составляющую из уравнения (1). Для этого необходимо решить характеристическое уравнение этой системы:

, тогда общее решение уравнения будет иметь вид:

(2)

где С₁ С₂,..., С_п – постоянные коэффициенты; p₁ р₂,…, р_п – корни характеристического уравнения системы.

Так как по условию задачи величина y_общ(0) с течением времени должна стремиться к нулю, то каждый член выражения (2) также должен стремиться к нулю. Для этого необходимо и достаточно, чтобы вещественная часть (действительные корни могут рассматриваться как частный случай комплексных корней с нулевой мнимой частью) всех корней характеристического уравнения была отрицательной. В этом случае показатели степени всех экспонент будут отрицательными, в результате чего с течением времени абсолютные значения всех экспоненциальных слагаемых будут стремиться к нулю.

Если хотя бы один корень характеристического уравнения имеет положительную или равную нулю вещественную часть, соответствующая составляющая переходного процесса будет неограниченно возрастать или совершать незатухающие колебания. Следовательно, система не сможет прийти в установившееся состояние, т.е. система будет неустойчивой.

Таким образом, чтобы ответить на вопрос, устойчива или неустойчива система, достаточно найти корни ее характеристического уравнения. Однако этим методом пользоваться во многих случаях практически невозможно, так как находить корни алгебраических уравнений высоких степеней очень трудно. Кроме того, найдя корни характеристического уравнения, мы определим, устойчива или неустойчива система, но не сможем установить, как нужно изменить параметры системы для обеспечения или повышения ее устойчивости, и представить себе, как те или иные параметры автоматической системы влияют на ее устойчивость. Поэтому желательно иметь критерии, с помощью которых можно судить об устойчивости системы непосредственно по коэффициентам характеристического уравнения без вычисления корней. Поэтому в теории автоматического регулирования и инженерной практике широко применяют косвенные методы исследования системы автоматического регулирования на устойчивость. Такие критерии называются критериями устойчивости.

Дата добавления: 2015-07-25