Электронно-дырочный П-Н переход. ВАХ.

Если к p - n -переходу приложить внешнее напряжение (U), то динамическое равновесие нарушится. Приложим к области p плюс, а к n – минус (рис. 1.13). Под действием этого напряжения, высота потенциального барьера Dj₀ уменьшится и станет равной Dj = Dj₀ – U, что приведет к возрастанию диффузионного тока, а так как этот ток определяется основными носителями, то величина и приращение этого тока будет большими, а величина напряжения и приращение этого напряжения малыми. Такое напряжение называется прямым напряжением на p - n -переходе, а ток – прямым током. При обратной полярности внешнего напряжения (рис. 1.14) высота потенциального барьера увеличивается Dj = Dj₀ + U, что приводит к возрастанию дрейфового тока, но так как этот ток определяется неосновными носителями, то величина его не может быть большой. Поэтому величина обратного напряжения большая, а ток близок к нулю. Такое напряжение и ток называются обратными.

Внешнее напряжение изменяет не только потенциал Dj, но и ширину обедненной области, а также зонную диаграмму на p - n -переходе. Для обратного напряжения ширина обедненной зоны будет увеличиваться

.

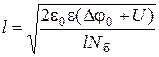Изменение ширины обедненной зоны при обратном напряжении происходит в основном за счет базовой области.

Зонная диаграмма на p - n -переходе при подключении внешнего напряжения тоже изменяется. При прямом напряжении искривление зон уменьшается, а при обратном – увеличивается.

1.9.4. Количественная оценка изменения концентрации

неосновных носителей в обедненной зоне

Изменение высоты потенциального барьера сопровождается, изменением граничных концентраций носителей (n_n, n_р, p_р, p_n), но так как n_n >> n_р, а p_р >> p_n, то можно считать, что меняются только неосновные носители. Считая, что внешнее напряжение приложено к обедненной области, найдем изменение n_р и р_n. Для равновесного состояния высота потенциального барьера 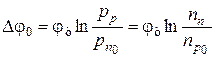, тогда

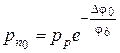, (1.13)

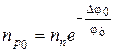. (1.14)

Подставим вместо 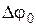его значение при подключении прямого напряжения Dj = Dj₀ – U, получим

,

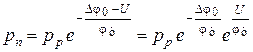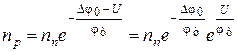
или

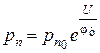, (1.15)

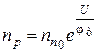. (1.16)

Как видно из (1.15) и (1.16), при прямых напряжениях концентрация неосновных носителей в обедненной области растет. Это явление носит название инжекции. Очевидно, если приложено обратное напряжение, то 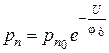, 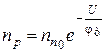. Следовательно, концентрация не основных носителей уменьшается и это явление носит название экстракция.

Избыточные концентрации при инжекции можно найти как разницу между 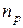и 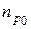, а также 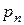и .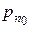

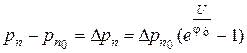, (1.17)

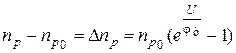. (1.18)

Найдем отношение избыточных концентрации при прямом напряжении 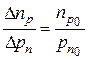, учитывая, что 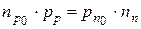, а отношение 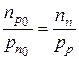, получим 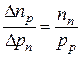, так как 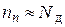, , 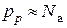то 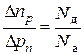, 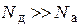. Переход несимметричный, следовательно, 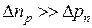, избыток электронов в р -области значительно больше избытка дырок в n -области, т.е. в несимметричных переходах инжекция носит односторонний характер. Главную роль играют носители, инжектируемые из эмиттера в базу. График изменения неосновных носителей в областях n и р представлена на рис. 1.15.

При выводе ВАХ делаем следующие допущения:

1. Током, вызванным рекомбинацией носителей на р - n -переходе, пренебрегаем. В этом случае мы считаем, что 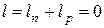. Если 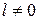, то обязательно будет рекомбинация части носителей в обедненной области, что вызовет дополнительную составляющую тока через переход.

2. Все внешнее напряжение U приложено только к обедненному слою n - p -перехода, т.е. на границах областей р и n электрическое поле равно нулю, тогда дрейфовый ток через переход тоже равен нулю.

Следовательно, ток инжектированных носителей носит чисто диффузионный характер.

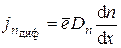
и

.

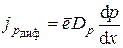Из рис. 1.15 видно, что производная в точке х = 0 может быть приближенно найдена так

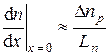
и

.

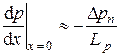Подставив значения 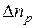и 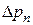из выражений(1.17) и (1.18), получим

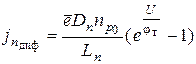
и

.

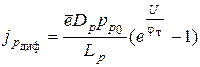Тогда полная плотность тока через переход

.

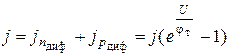Умножим плотность тока на площадь p - n -перехода, получим значение тока через переход

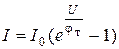, (1.19)

где 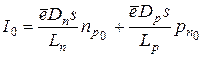называется обратным или тепловым током р - n -перехода.

Графическое изображение идеальной ВАХ представлено на рис. 1.16.

Эта характеристика построена по уравнению (1.19) и называется идеальной ВАХ. При комнатной температуре у кремневого транзистора величина I ₀» 10^–15А, а U _пр» 0,7–0,8 В. Однако величина этого тока очень сильно зависит от температуры. Зависимость I ₀ от температуры можно выразить следующей формулой

,

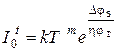где для Ge m = 2, h = 1, Dj_з = 0,76 В; для Si m = 1,5, h = 2, Dj_з = 1,11 В.

Для приближенных расчетов можно пользоваться формулой удвоения.

,

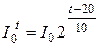т.е. на каждые 10° С ток увеличивается в два раза.

Как видно из формулы (1.19), I ₀ влияет на прямую и обратную ветвь, но т.к. ток в прямой ветви достаточно большой, то относительное увеличение не является существенным, а вот обратная ветвь меняется достаточно сильно. При предельных температурах (Ge = 85° C, Si = 125° C) обратный ток становится соизмерим с прямым током и переход перестает работать.

Дата добавления: 2015-07-25