
Читайте также:
|
ВИНЕСЕНИХ НА САМОСТІЙНЕ ОПРАЦЮВАННЯ
Експериментальна перевірка теореми Штейнера.
Миттєві (вільні) вісі обертання.
Гіроскопічний ефект і його застосування.
Важелі.
Умова рівноваги тіла кочення.
Наслідки рівняння Бернуллі.
Ефект. Магнуса.
Крило та парус.
Машина з обертовими лопостями.
Прості механічні коливні системи.
Резонанс, його роль в техніці.
Сприймання звуку.
Джерела і приймачі звуку.
Фізіологічна акустика. Модель вуха.
Джерела і приймачі звуку.
Ультразвук, застосування його в науці і техніці.
ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДО САМОСТІЙНОГО РОЗВ’ЯЗУВАННЯ ЗАДАЧ
Таблиця варіантів
| Номер варіанта | Номер задачі | |||||||||||||
Умови задач для самостійного розв’язування
1. Людина знаходиться у центрі горизонтальної круглої платформи, що обертається навколо осі, яка проходить через центр маси людини та центр маси платформи. Людина тримає в руках горизонтально штангу довжиною l = 2 м та масою m =18 кг. Платформа при цьому обертається з частотою ν = 0,1 с-1. Людина повертає штангу в вертикальній площині на кут φ = 60º. Визначити роботу, яку виконала при цьому людина. Момент інерції людини вважати еквівалентним масі m 0 = 50 кг, що знаходиться на відстані r 0 = 0,04 м від осі обертання. Момент інерції платформи не враховувати.
Відповідь: A = 85,7 Дж.
2. Горизонтальна платформа масою m 1 = 150 кг обертається навколо вертикальної осі, що проходить через центр платформи, з частотою ν 1 = 8 хв - 1. Людина масою m 2 = 70 кг стоїть при цьому на краю платформи. З якою кутовою швидкістю ω почне обертатися платформа, якщо людина перейде від краю платформи до її центру? Вважати платформу круглим, однорідним диском, а людину – матеріальною точкою.
Відповідь: ω = 1,62 рад/с.
3. На лаві Жуковського сидить людина і тримає у витягнутих руках два тягарі масою по m = 10 кг кожний. Відстань тягарів від осі обертання l= 0,5 м. Частота обертання лави з людиною ν = 1 с-1. Як зміниться частота обертання лави і яку роботу виконає людина, якщо вона перемістить руки так, що відстань від кожного тягаря до осі зменшиться до Δ x = 0,2 м? Момент інерції лави з людиною відносно осі обертання J = 2,5 кг×м2. Вісь обертання проходить через центр мас лави і людини.
Відповідь: ν1=2,3 с-1; A=190 Дж.
4. Платформа у вигляді суцільного диска радіусом R = 1 м масою M=240 кг обертається за інерцією навколо вертикальної осі з частотою ν = 0,1 с-1. На краю платформи стоїть людина масою m = 80 кг. З якою кутовою частотою обертатиметься платформа, якщо людина перейде в її центр? Людину вважати матеріальною точкою.
Відповідь: ω = 0,166 с-1.
5. Платформа у вигляді суцільного диска радіусом r = 1,5 м і масою M = 180 кг обертається за інерцією навколо вертикальної осі з частотою ν = 10 хв-1. У центрі платформи стоїть людина масою m =60 кг. Яку лінійну швидкість відносно підлоги приміщення буде мати людина, якщо вона перейде на край платформи? Момент інерції людини розраховувати як для матеріальної точки.
Відповідь: υ = 1 м/с.
6. Платформа, що має форму диска, може обертатися навколо вертикальної осі. На краю платформи стоїть людина. На який кут φ повернеться платформа, якщо людина піде уздовж краю платформи і, обійшовши її, повернеться у вихідну (на платформі) точку? Маса платформи m 1 = 280 кг, маса людини m2 = 80 кг.
Відповідь: φ = 0,73 p = 1310.
7. На лаві Жуковського стоїть людина і тримає в руці за вісь велосипедне колесо, що обертається навколо своєї осі з кутовою швидкістю ω1 = 25 рад/с. Вісь колеса розташована вертикально і збігається з віссю лави Жуковського. З якою швидкістю ω2 стане обертатися лава, якщо повернути колесо навколо горизонтальної осі на кут α = 90º? Момент інерції людини і лави дорівнює J = 2,5 кг×м 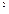 , момент інерції колеса j0 = 0,5 кг×м 2.
, момент інерції колеса j0 = 0,5 кг×м 2.
Відповідь: ω2 = 4,55 рад/с.
8. На краю платформи у вигляді диска, що обертається за інерцією навколо вертикальної осі з частотою ν 1 = 8 хв - 1, стоїть людина масою m 1 = 70 кг. Коли людина перейшла в центр платформи, вона стала обертатися з частотою ν 2 = 10 хв - 1. Визначити масу m 2 платформи. Момент інерції людини розраховувати як для матеріальної точки.
Відповідь: m 2 = 560 кг.
9. На краю нерухомої лави Жуковського діаметром D = 0,8 м і масою m1 = 6 кг стоїть людина масою m2 = 60 кг. З якою кутовою швидкістю ω почне обертатися лава, якщо людина зловить м'яч масою m = 0,5 кг, що летить на неї? Траєкторія м'яча горизонтальна і проходить на відстані r = 0,4 м від осі лави. Швидкість м'яча υ = 5 м/с.
Відповідь: ω = 0,1 рад/с.
10. На лаві Жуковського стоїть людина і тримає в руках стрижень довжиною l = 2,4 м і масою т = 8 кг, розташований вздовж осі обертання лави. Лава з людиною обертається з частотою ν 1= 1 c-1. З якою частотою ν 2 буде обертатися лава з людиною, якщо стрижень повернути у горизонтальне положення? Сумарний момент інерції J людини і лави дорівнює 6 кг·м2.
Відповідь: ν 2 = 0,61 c-1.
11. На краю горизонтальної платформи, що має форму диска радіусом R = 2 м, стоїть людина масою m1 = 80 кг. Маса платформи дорівнює т2 =240 кг. Платформа може обертатися навколо вертикальної осі, що проходить через її центр. Нехтуючи тертям, знайти, з якою кутовою швидкістю ω буде обертатися платформа, якщо людина буде йти вздовж її краю із швидкістю υ = 2 м/с відносно платформи.
Відповідь: ω = 0,445 рад/с.
12. Платформа у вигляді диска радіусом R = 1 м обертається за інерцією з частотою ν 1 = 6 хв-1. На краю платформи стоїть людина, маса т якої дорівнює 80 кг. З якою частотою ν 2 буде обертатися платформа, якщо людина перейде в її центр? Момент інерції платформи дорівнює J = 120 кг·м2. Момент інерції людини розраховувати як для матеріальної точки.
Відповідь:ν 2 = 10 хв-1.
13. Людина масою m = 60 кг, що стоїть на краю горизонтальної платформи масою M = 120 кг, яка обертається за інерцією навколо нерухомої вертикальної осі з частотою ν 1 = 10 хв-1, переходить до її центра. Вважаючи платформу круглим однорідним диском, а людину – точковою масою, визначити, з якою частотою ν 2буде обертатися платформа.
Відповідь: ν 2= 20 хв-1.
14. Людина масою m = 60 кг, що стоїть на краю горизонтальної платформи радіусом R = 1 м і масою M = 120 кг, яка обертається за інерцією навколо нерухомої вертикальної осі з частотою n1 = 10 хв-1, переходить до її центра. Вважаючи платформу круглим однорідним диском, а людину – точковою масою, визначити, яку роботу здійснить людина при переході від краю платформи до її центра.
Відповідь: А = 65,8 Дж.
15. Горизонтальна платформа масою m = 100 кг обертається навколо вертикальної осі, що проходить через центр платформи, з частотою n 1 = 10 об/хв. Людина масою m 0 = 60 кг стоїть на краю платформи. З якою частотою n2 почне обертатися платформа, якщо людина перейде від краю платформи до її центру? Вважати платформу однорідним диском, а людино – точковою масою.
Відповідь: n2 = 21 об/хв.
16. На яку відстань по дорозі під гору може вкотитися обруч за рахунок своєї кінетичної енергії, якщо перед цим він мав швидкість υ = 2 м/с, а нахил дороги становить h = 10 м на кожні S = 100 м шляху? Тертя не враховувати.
Відповідь: S = 4,08 м.
17. Диск масою m = 2 кг котиться без ковзання по горизонтальній поверхні зі швидкістю υ = 2 м/с. На якій відстані можна його зупинити, приклавши до обода силу F = 9,8 Н?
Відповідь: S = 0,82 м.
18. Куля масою 1 кг, що котиться без ковзання зі швидкістю υ = 10 м/с, вдаряється об стінку та відскакує від неї зі швидкістю u = 8 м/с. Знайти кількість теплоти, що виділяється під час удару.
Відповідь: Q = 25,2 Дж.
19. Повна кінетична енергія диска, що котиться по горизонтальній поверхні, дорівнює EK = 24 Дж. Знайти кінетичну енергію поступального і обертального рухів диска.
Відповідь: Е пос = 16 Дж; Е об = 8 Дж.
20. Куля котиться без ковзання по горизонтальній поверхні. Повна кінетична енергія кулі дорівнює EK = 14 Дж. Визначити кінетичну енергію Е пос поступального і Е об обертального руху кулі.
Відповідь: Е пос=10 Дж; Е об =4 Дж.
21. Момент інерції маховика J = 0,1 кг×м2. Через який час маховик матиме частоту обертання ν = 30 с-1, якщо корисна потужність двигуна N = 100 Вт.
Відповідь: t = 3,9 с.
22. Шків, насаджений на вісь електродвигуна, обертається з кутовою швидкістю ω = 93 с-1. Після вимкнення двигуна шків, зробивши N = 20 обертів, зупинився. Момент інерції шківа j = 0,01 кг×м2. Знайти момент сил гальмування та їх роботу.
Відповідь: M = 9,4 10-2 Н×м; A = - 44,4 Дж.
23. До ободу однорідного диска масою m = 10 кг, насадженого на вісь, прикладена стала дотична сила F = 30 Н. Визначити кінетичну енергію диска через t = 4 с після початку дії сили.
Відповідь: EK = 1,44 кДж.
24. Маховик у вигляді диска масою т = 80 кг і радіусом R = 30 см перебуває у стані спокою. Яку роботу A1 потрібно виконати, щоб надати маховику частоту ν = 10 с-1? Яку роботу А2 довелося б виконати, якби при тій самій масі диск мав меншу товщину, але вдвічі більший радіус?
Відповідь: А1 = 7,11 кДж; А2 = 28,4 кДж.
25. Через блок, що має форму диска, перекинутий шнур. До кінців шнура прив'язали тягарці масою т1 = 100 г і т2 = 110 г. З яким прискоренням а будуть рухатися тягарці, якщо маса т блока дорівнює 400 г? Тертям при обертанні блока знехтувати.
Відповідь: а = 0,24 м/с2.
26. До ободу однорідного диску радіусом R = 0,2 м прикладена дотична сила F = 98,1 Н. Під час обертання на диск діє момент сил тертя М ТР = 4,9 Н∙м. Знайти масу диска, якщо відомо, що диск обертається з кутовим прискоренням β = 100 рад/с2.
Відповідь: т = 7,36 кг.
| 27. Два тіла масами т1 = 0,25 кг і т2 = 0,15 кг зв'язані тонкою ниткою, перекинутою через блок (рис. 7.1). Блок закріплений на краю горизонтального стола, по поверхні якого ковзає тіломасою т1. | 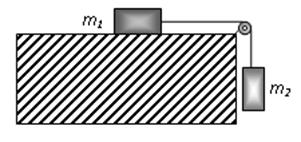
|
| Рис. 7.1. |
З яким прискоренням а рухаються тіла і чому дорівнюють сили Т натягу нитки по обидва боки від блока? Коефіцієнт тертя тіла об поверхню стола дорівнює μ = 0,2.Маса блока дорівнює т = 0,1 кг і її можна вважати рівномірно розподіленою вздовж обода. Масою нитки і тертям у підшипниках осі блока знехтувати.
Відповідь: а = 1,96 м/с2; Т1 = 0,98 Н; Т2 = 1,18 Н.
28. Маховик, момент інерції якого J = 63,6 кг∙м2, обертається з кутовою швидкістю ω = 31,4 рад/с. Знайти момент сил гальмування М, під дією якого маховик зупиняється через час t = 20 с. маховик вважати однорідним диском.
Відповідь:М =100 Н∙м.
29. Дві гирі масами т1 = 2 кг і т2 = 1 кг з’єднані ниткою, що перекинули через блок масою т = 1 кг. Знайти прискорення, з яким рухаються гирі та сили натягу Т1 і Т2 ниток, до яких підвішені гирі. Блок вважати однорідним диском. Тертям знехтувати.
Відповідь:Т1 = 14 Н, Т2 = 12,6Н.
30. Дві гирі з різними масами з’єднані ниткою, що перекинули через блок, момент інерції якого J = 50 кг∙м2 та радіус R = 20 см. момент сил тертя блока, що обертається М ТР = 98,1 Н∙м. Знайти різницю сил натягу нитки Т1 – Т2 по обидві сторони блока, якщо відомо, що блок обертається з кутовим прискоренням β = 2,36 рад/с2. Блок вважати однорідним диском.
Відповідь:Т1 – Т2 = ( J∙β + М ТР )/ R = 1,08 кН.
31. Однорідний стрижень довжиною l = 1м може вільно обертатися навколо горизонтальної осі, що проходить через один з його кінців. Коли він висить горизонтально, в інший кінець абсолютно непружно вдаряє куля масою m = 7 г, що летить перпендикулярно до стрижня і його осі. Визначити масу M стрижня, якщо в результаті влучення кулі він відхилиться на кут α = 60º. Швидкість кулі υ = 360 м/с.
Відповідь: М = 1,97 кг.
32. Визначити момент інерції труби масою M = 10 кг відносно осі симетрії, якщо внутрішній і зовнішній радіуси труби відповідно дорівнюють R1 = 5 см, R2 = 8 см.
Відповідь: J = 0,02 кг×м2.
33. Обчислити момент інерції J прямокутника з дроту із сторонами а = 12 см і b = 16 см відносно осі, що лежить у площині прямокутника і проходить через середини малих сторін. Маса рівномірно розподілена по довжині дроту з лінійною густиною τ = 0,1 кг/м.
Відповідь: J= 1,44 10-4 кг×м2.
34. Знайти момент інерції J тонкого однорідного кільця радіусом R = 20 см і масою т = 100 г відносно осі, що лежить у площині кільця і проходить через його центр.
Відповідь: J = 0,002 кг×м2.
35. Визначити момент інерції J тонкого однорідного стрижня довжиною l = 30 см і масою т = 100 г відносно осі, перпендикулярної до стрижня, яка проходить через: а) його кінець; б) його середину; в) точку, що віддалена від кінця стрижня на 1/3 його довжини.
Відповідь: а) J = 3×10-3 кг×м2; б) J = 0,75×10-3 кг×м2;в) J = 10-3 кг×м2.
36. Тонкий однорідний стрижень довжиною l = 50 см і масою т = 400 г обертається з кутовим прискоренням ε = 3 рад/с2 навколо осі, що проходить перпендикулярно до стрижня через його середину. Визначити обертальний момент М.
Відповідь: М = 0,025 Н×м.
37. Визначити момент інерції труби масою M = 100 кг відносно осі симетрії, якщо внутрішній і зовнішній радіуси труби відповідно дорівнюють R1 = 8 см, R2 = 10 см.
Відповідь: J = 0,36 кг×м2.
38. Однорідний стрижень довжиною l = 1м та масою m = 0,5 кг обертається у вертикальній площині навколо горизонтальної осі, що проходить через середину стрижня. З яким кутовим прискоренням ε обертається стрижень, якщо на нього діє момент сил М = 98,1 мН∙м?
Відповідь: β = 2,35 рад/с2.
39. Однорідний стрижень довжиною l = 1м підвішений на горизонтальній осі, що проходить через верхній кінець стрижня. На який кут α слід відхилити стрижень, щоб нижній кінець стрижня при проходженні положення рівноваги мав швидкість υ = 5 м/с?
Відповідь: α = 81°21'.
40. Однорідний стрижень довжиною l = 85 см підвішений на горизонтальній осі, що проходить через верхній кінець стрижня. Яку швидкість υ слід надати нижньому кінцю стрижня, щоб він зробив повний оберт навколо осі?
Відповідь: υ = 7,1 м/с.
41. Олівець довжиною l = 15 см, поставлений вертикально, падає на стіл. Яку кутову швидкість ω та лінійну швидкість υ будуть мати у кінці падіння середина і верхній кінець олівця?
Відповідь: ω 1= ω2 = 14 рад/с; υ1 = 1,05 м/с, υ2 = 2,10 м/с.
42. Суцільний сталевий циліндр радіусом R = 0,1 м та висотою h = 0,5 м обертається із сталою швидкістю ω = 2 рад/с навколо вертикальної осі Z, що проходить через одні з твірних циліндра. Визначити: 1) момент інерції циліндра J Z; 2) імпульс циліндра р; 3) момент імпульсу L Z; 4) кінетичну енергію.
Відповідь: J Z = 1,8 кг∙м2; р = 24,5 кг∙м/с; L Z = 5 кг∙м2/с; ЕК = 3,675 Дж.
43. Чому дорівнює момент імпульсу шліфувального круга у вигляді однорідного диску масою m = 2,3 кг та радіусом R = 12 см, що обертається з частотою n = 1500 об/с? Визначити, якої величини момент сил опору слід прикласти, щоб зупинити круг за t = 7 с.
Відповідь: М = 0,37 Н.
44. Дресирована собака масою m 1 = 10 кг заплигнула на тонкий полий горизонтальний циліндр масою m 2 = 5 кг, радіусом R = 0,3 м та шириною b = 0,2 м. Потім «артистка» стала перебирати лапами, так що весь час залишалась у верхній точці циліндру, надаючи їй постійної лінійної швидкості υ = 0,2 м/с. Визначити кінетичну енергію системи «собака - циліндр».
Відповідь: Е К = 0,3 Дж.
45. Стрижень масою 200 г зігнули посередині під прямим кутом та підвісили на нитці, прив’язаної до одного з кінців. Якої маси вантаж слід закріпити на іншому кінці, щоб середина нижньої половини стрижня знаходилася точно під точкою підвісу?
Відповідь m = 20 г.
46. Суцільна однорідна куля плаває на межі поділу двох не змішуваних рідин, густини яких дорівнюють відповідно ρ1 = 800 кг/м3 і ρ2 = 1000 кг/м3. Визначити густину тіла, якщо у верхній рідині знаходиться 0,30 об'єму кулі.
Відповідь: ρ = 940 кг/м3.
47. Знайти максимальне значення сили Архімеда, що діє на тіло у рідині з густиною 1,5∙103 кг/м3, якщо вага цього тіла в рідині густиною 2,5 кг/м3 становила 55 Н, а в рідині густиною 3,5∙103 кг/м3 - 25 Н.
Відповідь: FA = 45 Н.
48. Крижина площею поперечного перерізу S = 1 м2 і висотою h = 0,4 м плаває у воді. Яку роботу потрібно виконати, щоб повністю занурити крижину у воду?
Відповідь: A ≈ 7,84 Дж.
49. Один кінець рибальської волосіні закріплено на дні, а другий прикріплено до коркового поплавка. При цьому 0,55 об'єму поплавка занурено у воду. Визначити натяг волосіні, якщо маса поплавка m = 1 кг, а густина корка ρк = 0,25 кг/м3. Масою волосіні знехтувати.
Відповідь: T = 11,77 Н.
50. Крижина рівномірної товщини плаває у воді, висовуючись зовні на 2 см. Знайти масу крижини, якщо площа її основи 200 см2.
Відповідь: m = 4,6 кг.
51. З якої висоти має впасти тіло, густина якого 500 кг/м3, щоб зануритись у воду на глибину 10 см? Опором води і повітря знехтувати.
Відповідь: h = 10 м.
52. Однорідне тіло плаває на поверхні спирту так, що об'єм зануреної частини становить 0,92 всього об'єму тіла V. Визначте об'єм зануреної частини під час плавання цього тіла на поверхні води.
Відповідь: 0,736 V.
53. У склянку діаметром 5 см налито 314 г води. На скільки підвищиться рівень води в склянці і чому буде дорівнювати тиск на дно, якщо в склянку опустити сосновий кубик об'ємом 31,4 см3? Атмосферний тиск нормальний.
Відповідь: Δ h ≈ 1,3 см, p = 761 мм рт. ст.
54. У склянці перерізом 27 см2 плаває сосновий кубик об'ємом 27 см3. Яку мінімальну роботу потрібно виконати, щоб кубик повністю занурити у воду?
Відповідь: A ≈ 0,033 Дж.
55. Яку роботу треба виконати під час повільного підняття каменя об'ємом 0,5 м3 у воді з глибини 1 м?
Відповідь: A = 73,4∙103 Дж.
56. У пробірці з водою плаває сосновий кубик об'ємом 1 см3. Як зміниться рівень води в пробірці, якщо її піднімати вертикально вгору з прискоренням 4,9 м/с2? Опускати з таким самим прискоренням?
Відповідь: в усіх випадках кубик занурено на глибину 0,5 см.
57. Повітряна куля об'ємом V = 20 м3, заповнена гелієм, піднялася на висоту h = 180 м за час t = 0,5 хв. Маса кулі з обладнанням і кошиком M = 12 кг. Знайти масу вантажу, піднятого кулею. Густину повітря і гелію до висоти 180 м вважати сталими: ρп = 1,29 кг/м3, ρHe = 0,18 кг/м3.
Відповідь: m = 9,5 кг.
58. Стальна кулька плаває в ртуті. Яка частина об'єму кульки буде знаходитися в ртуті, якщо поверх неї налити шар води, що повністю покриває кулю?
Відповідь: 0,55.
59. Знайти вагу тіла в рідині з густиною ρ1 = 1,5∙103 кг/м3, якщо вага цього тіла в інших двох рідинах з густинами ρ2 = 103 кг/м3 і ρ3 = 2∙103 кг/м3 дорівнювала відповідно 55 Н і 30 Н.
Відповідь: P 1 = 42,5 Н.
60. Стальна порожниста куля плаває у воді, занурившись наполовину. Знайти об'єм внутрішньої порожнини кулі, якщо її маса m = 6 кг, а густина сталі ρ = 7,8×103 кг/м3
Відповідь: V = 11,2 10-3 м3.
61. Горизонтальний циліндр насоса має діаметр d1 = 20 см. У ньому рухається із швидкістю υ1 = 1 м/с поршень, виштовхуючи воду через отвір діаметром d2 = 2 см. З якою швидкістю υ2 буде витікати вода з отвору? Яким буде надлишковий тиск Р води в циліндрі?
Відповідь: υ2 = 100 м/с; Р = 5 МПа.
62. Водою і мазутом заповнений вертикально розміщений циліндричний бак. Висота води у баку H = 1 м, густина мазуту ρ = 900 кг/м3. У дні бака зроблено отвір, через який витікає вода з швидкістю υ = 9,5 м/с. Знайти висоту шару мазуту в баку.
Відповідь: h = 4 м.
63. У посудину щосекунди наливають V = 0,2 л води. Який повинен бути діаметр отвору в дні посудини, щоб вода в ній знаходилась на сталому рівні h = 83×10-3 м?
Відповідь: d = 14×10-3 м.
64. Площа поршня, вставленого у горизонтально розміщений заповнений водою шприц, S1 = 1,5 10-4 м2, а площа отвору його голки S2 = 0,8 10-6 м2. Нехтуючи тертям і в'язкістю, визначити час, за який витече вода із шприца, якщо на поршень діяти із сталою силою F = 5 Н, а хід поршня l = 5·10-2 м.
Відповідь: t = 1,15 с.
65. Рідина виштовхується поршнем шприца площею S1 = 2 10-4 м2 через отвір голки площею S2=1,5 10-6 м2. Хід поршня становить l = 8 10-2 м. Знайти тиск на поршень, якщо рідина витікає з нього протягом τ = 3 с. Шприц розміщений горизонтально, а рідина, густина якої ρ = 1840 кг/м3, перебуває під атмосферним тиском.
Відповідь: P = 40 Па.
66. У бокову поверхню циліндричного бака радіусом R = 0,02 м вставили горизонтальний капіляр довжиною l = 0,02 м та радіусом r =0,001 м. В бак налито касторове масло, динамічна в'язкість якого 1,2 Па×с. Знайти залежність швидкості опускання рівня касторового масла в баку від висоти цього рівня над капіляром та обчислити її значення для висоти рівня h = 0,26 м.
Відповідь: υ = 3 10-5 м/с.
67. У бокову поверхню посудини вставили горизонтальний капіляр довжиною l = 0,012 м та діаметром d = 0,002 м. Через капіляр витікає касторове масло, густина якого ρ = 960 кг/м3, динамічна в'язкість 0,99 Па×с. Рівень масла у посудині підтримується на сталій висоті h = 0,3 м вище капіляра. Визначити час, протягом якого через капіляр витече V = 10-5 м3 масла.
Відповідь: t = 107 с.
68. У стінці посудини з водою зробили два отвори на відстані Δ l = 0,2 м один над одним площею S = 2 см2 кожний. Визначити координати точки перетину потоків, що витікають з отворів, якщо у посудину щосекунди вливається V = 1,4 дм3 води.
Відповідь: х = 1,2 м; у = 1,3 м.
69. У посудину щосекунди наливають V = 0,2 л води. Який повинен бути діаметр отвору в дні посудини, щоб вода в ній знаходилась на сталому рівні h = 83×10-3 м?
Відповідь: d = 14×10-3 м.
70. Бак висотою H = 1,5 мм наповнений доверху водою. На відстані h = 1 м від верхнього краю бака утворився отвір малого діаметра.
На якій відстані l від бака падає на підлогу струмінь, що витікає з отвору?
Відповідь: l =1,4 м.
| 71. Струмінь води з площею поперечного перерізу S1 = 4 см витікає горизонтально з брандспойта, який розміщено на висоті H = 2 м над поверхнею землі, і падає на цю поверхню на відстані l = 8 м (рис. 7.2). | 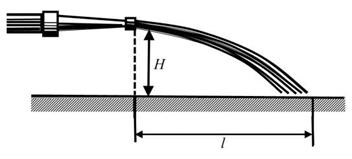
|
| Рис. 7.2 |
Нехтуючи опором повітря руху води, знайти надлишковий тиск p води в рукаві, якщо площа поперечного перерізу рукава дорівнює S2 = 50 см?
Відповідь: p = 77,9 кПа.
72. Бак висотою H = 2 м доверху заповнений рідиною. На якій висоті h повинен бути зроблений отвір у стінці бака, щоб місце падіння струменя, який витікає з отвору, було на максимальній від бака відстані?
Відповідь: h = 1 м.
73. Горизонтальний циліндр насоса має діаметр d1 = 20 см. У ньому рухається зі швидкістю u1 = 1 м/с поршень, що виштовхує воду через отвір діаметром d2 = 2 см. З якою швидкістю υ2 витікатиме вода з отвору? Який буде надлишковий тиск p води у циліндрі?
Відповідь: υ2 = 100 м/с, p = 5 МПа.
74. Широка посудина з невеликим отвором у дні наповнена водою і гасом. Товщина шару води h1 = 30 см, а шару гасу h2 = 20 см. Нехтуючи в'язкістю, знайти швидкість води, що витікає з отвору. Густина ρ1 = 1000 кг/м3, ρ1 = 800 кг/м3.
Відповідь: υ = 3 м/с.
75. Струмінь води діаметром d =2 см рухається зі швидкістю υ =10 м/с, падає на нерухому плоску поверхню, розміщену перпендикулярно до струменя. Знайти силу F тиску струменя на поверхню, вважаючи, що після падіння струменя на поверхню швидкість частинок води дорівнює нулю.
Відповідь: F =31,4 Н.
| 76. Зігнуту трубку опустили в потік води, як показано на рис. 7.3. Швидкість потоку відносно трубки υ =2,5 м/с. Закритий верхній кінець трубки має невеликий отвір і знаходиться на висоті h0 =12 см. На яку висоту h підніматиметься струмінь води, що витікає з отвору? Відповідь: h = υ2 / 2 g - h0 =20 см. | 
|
| Рис. 7.3. |
77. Тиск p вітру на стіну дорівнює 200 Па. Визначити швидкість υ2 вітру, якщо він дме перпендикулярно до стіни. Густина ρ повітря дорівнює 1,29 кг/м3 .
Відповідь: υ =8,80 м/с.
78. Вода тече по круглій трубі діаметром d =5 см з середньою в перерізі швидкістю (υ =10 см/с. Визначити число Рейнольдса Rе для потоку рідини в трубі і визначити характер течії рідини. Критичне число Рейнольдса ReKp = 2300, в'язкість води η = 1,0 мПа∙с.
Відповідь: Re = p(υ)d/ h =5000; Re > Re Кр, тому рух турбулентний.
79. У трубі з внутрішнім діаметром d =3 см тече вода. Визначити максимальну масову витрату Qm води за умови ламінарної течії. Критичне число Рейнольдса ReKp = 2300, в'язкість води η = 1,0 мПа∙с.
Відповідь: Qm max =πηReКр d /4 = 54,2 г/с.
80. Струмінь води діаметром d = 2 см, що рухається зі швидкістю υ = 10 м/с, вдаряється об нерухому плоску поверхню, перпендикулярну до струменя. Визначити силу F тиску струменя на поверхню, вважаючи, що після удару об поверхню швидкість частинок води дорівнює нулю.
Відповідь: F = 31,4 Н.
81. Вода тече по трубі, причому за одиницю часу через поперечний переріз труби протікає об’єм води V t =200 см3/с. Динамічна в’язкість води η = 0,001 Па∙с. При якому граничному значенні діаметру D труби рух води залишається ламінарним (ламінарність руху рідини в циліндричні трубі зберігається при числі Рейнольдса Rе ≤ 3000, якщо при розрахунку Rе у якості величини D взяти діаметр труби).
Відповідь:Число Рейнольдса Rе = 1800.
| 82.Водомір - це горизонтальна труба змінного перерізу, в яку впаяні дві вертикальні манометричні трубки однакового перерізу (рис. 7.4). По трубі тече вода. Нехтуючи в'язкістю води, визначити її масову витрату, якщо різниця рівнів у манометричних трубках Δh =00,8 мм, а перерізи труби біля основ манометричних трубок відповідно дорівнюють 6×10-4 м2 і 12×10-4 м2. | 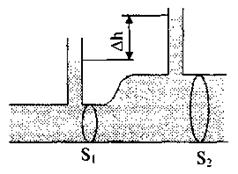
|
| Рис. 7.4. |
Відповідь:ΔQ = 868 10-3 кг/с.
83. За час t = 1 с через поперечний переріз труби протікає V = 0,5 л води. Динамічна в’язкість води за даних умов h = 10-3 Н×с/м2, число Рейнольдса Re кр = 3000. При якому діаметрі труби рух води залишається ламінарним?
Відповідь: d = 20 см.
84. Вода тече по горизонтальній трубі змінного перерізу. Швидкість води в широкій частині труби дорівнює υ1 = 10 см/с. Визначити швидкість υ2 у вузькій частині труби, радіус R2 якої в 3 рази менше радіуса широкої частини.
Відповідь: υ2 =90 см/с.
85. Вода тече в горизонтально розміщений трубі змінного перерізу. Швидкість υ1 води в широкій частині труби дорівнює 20 см/с. Визначити швидкість υ2 у вузькій частині труби, діаметр d2 якої в 1,5 рази менше за діаметр d1 широкої частини.
Відповідь: υ2=0,45 м/с.
86. У широкій частині горизонтально розміщеної труби нафта тече із швидкістю υ1 = 2 м/с. Визначити швидкість υ2 нафти у вузькій частині труби, якщо різниця Δp тиску в її широкій і вузькій частинах дорівнює 6,65 кПа.
Відповідь: υ2 = 4,33 м/с.
87. У горизонтально розміщеної трубі з площею S1 поперечного перерізу, що дорівнює 20 см, тече рідина. В одному місці труба має звуження, в якому площа S2 перерізу дорівнює 12 см2. Різниця Δh рівнів у двох манометричних трубках, встановлених у широкій і вузькій частинах труби, дорівнює 8 см. Визначити об'ємну витрату QV рідини.
Відповідь: QV = 1,88 л/с.
88. Знайти швидкість υ течії вуглекислого газу по трубі, якщо відомо, що за час t = 30 хв. Через поперечний переріз труби протікає маса газу m = 0,51 кг. Густина газу ρ = 7,5 кг/м3. Діаметр труби D = 2 см.
Відповідь: υ = 0,12 м/с.
89. Який тиск Р створює компресор у фарбопульті, якщо потік рідкої фарби витікає з нього із швидкістю υ = 25 м/с? Густина фарби ρ = 0,8∙10 3 кг/м3.
Відповідь: Р = 250 кПа.
| 90. По горизонтальній трубі АВ тече рідина (рис. 7.5). Різниця рівнів цієї рідини у трубках а та b дорівнює Δh = 10 см. Діаметри трубок а та b однакові. Знайти швидкості υ течії рідини в трубі АВ. Відповідь: υ = 1,4 м/с. | 
|
| Рис. 7.5 |
91. Мідна кулька діаметром d=1 см падає зі сталою швидкістю у касторовій олії. Чи є рух олії, викликаний падінням у ньому кульки, ламінарним? Критичне число Рейнольдса ReKp =0,5, в'язкість касторової олії h = 987 мПа-с, густина міді р1 = 8930 кг/м3, густина касторової олії р2 = 960 кг/м3.
Відповідь: Re =ρ1 (ρ1 – ρ 2)gd3/(l8η2)=4,17; Re > Re кр р турбулентний.
92. Кулька спливає с постійною швидкістю υ у рідині, густина ρ 1 якої у 4 рази більше густини ρ2 матеріалу кульки. У скільки разів сила тертя F ТР, що діє на спливаючу кульку, більша за силу тяжіння mg, що діє на цю кульку?
Відповідь: F ТР/ mg = 3.
93. Якої найбільшої швидкості υ може досягнути дощова краплина діаметром d = 0,3 мм, якщо динамічна в’язкість повітря η = 1,2∙10 – 5 Па∙с?
Відповідь: υ = 4,1 м/с.
94. Сталева кулька діаметром d = 1 мм падає з постійною швидкістю υ = 0,185 см/с у великій посудині, заповненій касторовим маслом. Знайти динамічну в’язкість η касторового масла.
Відповідь: η = 2 Па∙с
95. Суміш свинцевих дробинок з діаметрами d1 = 3 мм та d2 = 1 мм опустили в бак з гліцерином висотою h = 1 м. На скільки пізніше впадуть на дно дробинки меншого діаметру порівняно з дробинками більшого діаметру? Динамічна в’язкість гліцерину η = 1,47 Па∙с.
Відповідь: Δt = 4 хв.
96. Пробкова кулька радіусом r = 5 мм спливає у посудині, наповненій касторовим маслом. Знайти динамічну та кінематичну в’язкість касторового масла, якщо кулька спливає з постійною швидкістю υ = 3,5 см/с.
Відповідь: η = 1,09 Па∙с, ν = 12,1 см2/с.
97. Мідна кулька діаметрами d = 1 см падає з постійною швидкістю у касторовому маслі. Чи є рух масла, що викликано падінням в ньому кульки, ламінарним, якщо для кульки Rе КР = 0,5?
Відповідь: Rе = 0,385 < Rе КР, рух ламінарний.
98. Вантажний автомобіль рухається зі швидкістю υ = 6 км/год. Яка потужність по подоланню опору повітря, якщо рух є турбулентним? Площина міделя автомобіля складає 3,75 м 2. Прийняти, що С х = 0,6 та густина повітря дорівнює 1,2 кг/м3.
Відповідь: N = 12,5 кВт.
99. Латунна кулька діаметром d = 0,6 мм падає в гліцерині. Визначити: 1) швидкість υ сталого руху кульки; 2) чи є обтікання кульки ламінарним? Критичне число Рейнольдса ReKp = 0,5, в'язкість гліцерину η = 1480 мПа-с, густина латуні ρ1 = 8550 кг/м3, густина гліцерину ρ2 = 1260 кг/м3.
Відповідь: υ = (ρ1 – ρ 2)gd2/(l8η) = 6,71 мм/с; 2) обтікання кульки ламінарне.
100. Під час руху кульки радіусом r1 = 2,4 мм у касторовій олії ламінарне обтікання спостерігається при швидкості υ1 кульки, що не перевищує 10 см/с. При якій мінімальній швидкості υ2 кульки радіусом r2 = 1 мм у гліцерині обтікання стане турбулентним? В'язкість касторової олії η1 = 987 мПа∙с, густина - ρ1 = 960 кг/м3; в'язкість гліцерину η2 = 1480 мПа∙с, густина - ρ2 = 1260 кг/м3.
Відповідь: υ2 = 27,7 см/с.
101. Свинцева кулька рівномірно опускається в гліцерині, в'язкість якого η =1,48 Па∙с. При якому найбільшому діаметрі кульки його обтікання ще залишається ламінарним? Відомо, що перехід до турбулентного обтікання відповідає числу ReKp = 0,5, густина свинцю ρ = 11300 кг/м3, густина гліцерину ρ0 = 1260 кг/м3.
Відповідь: d = 5,4 мм.
102. Сталева кулька діаметром d = 3,0 мм опускається з нульовою початковою швидкістю у оливковій олії, в'язкість якої η = 90 м∙Па∙с. Через який час після початку руху швидкість кульки відрізнятиметься від сталого значення на n = 1,0 %?
Відповідь: t = 0,20 с.
103. У посудині, заповненій касторовим маслом, падає стальна кулька зі сталою швидкістю υ = 0,2 м/с.
Динамічна в'язкість касторового масла 2 Н×с/м2. Визначити радіус кульки.
Відповідь: r = 0,5 10-3 м.
104. Кулька спливає із сталою швидкістю в рідині, густина якої в три рази більша від густини матеріалу кульки. Знайти відношення сили тертя, що діє на кульку, до її ваги.
Відповідь: n=2.
105. Визначити найбільшу швидкість, яку може розвинути вільно падаюча у повітрі (густина 1,29 кг/м3) свинцева кулька (густина 11300 кг/м3) масою m=0,012 кг. Коефіцієнт лобового опору дорівнює f = 0,5.
Відповідь: υ = 77,6 м/с.
106. Матеріальна точка здійснює прості гармонічні коливання так, що в початковий момент часу зміщення становить х0 = 4 см, а швидкість u 0 = 10 см/с. Визначити амплітуду А і початкову фазу φ 0 коливань, якщо їх період становить Т = 2 с.
Відповідь: A = 5,13 см; φ 0 = 390.
107. Коливання матеріальної точки відбуваються згідно з рівнянням х = Асоs  t, где А= 8 см; ω = π/6 с-1. В момент, коли повертальна сила вперше досягла значення F = 5 мН, потенціальна енергія точки стала дорівнювати E Р=100 мкДж. Знайти цей момент часу t і відповідну йому фазу ωt.
t, где А= 8 см; ω = π/6 с-1. В момент, коли повертальна сила вперше досягла значення F = 5 мН, потенціальна енергія точки стала дорівнювати E Р=100 мкДж. Знайти цей момент часу t і відповідну йому фазу ωt.
Відповідь: t = 2 с; ωt =  .
.
108. Точка виконує коливання за законом х = А соs 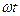 , де А =5 cм; ω=2 с-1 Визначити прискорення |а| точки у момент часу, коли її швидкість u = 8 см/с.
, де А =5 cм; ω=2 с-1 Визначити прискорення |а| точки у момент часу, коли її швидкість u = 8 см/с.
Відповідь: a = 12 см/с2.
109. Знайти повертальну силу F у момент часу t = 1 с і повну енергію Е матеріальної точки, яка бере участь у коливаннях що відбуваються за законом х=Аcos 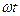 , де А= 20 cм; ω =2
, де А= 20 cм; ω =2  /3 с-1. Маса матеріальної точки дорівнює m= 10 г.
/3 с-1. Маса матеріальної точки дорівнює m= 10 г.
Відповідь: F= 4,39 мН; E = 880 мкДж.
110. Матеріальна точка здійснює коливання за законом  , де А =2 м. Визначити початкову фазу, якщо в момент часу t = 0 зміщення x = -
, де А =2 м. Визначити початкову фазу, якщо в момент часу t = 0 зміщення x = -  м.
м.
Відповідь:  .
.
111. Амплітудне значення швидкості матеріальної точки, що здійснює гармонічні коливання, υ max = 0,1 м/с, а максимальне прискорення a max = 1 м/с2.Визначити циклічну частоту, період та амплітуду коливань.
Відповідь:ω = 10 с-1; T = 0,629 с; A = 0,01 м.
112. Матеріальна точка здійснює гармонічні коливання з частотою ν = 1 Гц і в момент часу t = 0 проходить положення з координатою x = 0,05 м зі швидкістю υ = 0,15 м/с. Визначити амплітуду коливань.
Відповідь: A = 0,0554 м.
113. Кулька масою m = 0,02 кг здійснює гармонічні коливання за законом 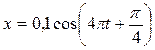 м. Визначити повну енергію кульки.
м. Визначити повну енергію кульки.
Відповідь: E = 15,8 мДж.
114. Точка здійснює прості гармонічні коливання, рівняння яких мають вигляд х= А sinωt, де А =5 см, ω = 2 с-1. У момент часу, коли точка мала потенціальну енергію Еп =0,1 мДж, на неї діяла повертальна сила F =5 мН. Знайти цей момент часу t.
Відповідь: t = 1,5 с.
115. Коливання матеріальної точки масою m = 0,1 г відбуваються відповідно до рівнянь х = A coswt де А = 5см, ω= 20 с-1. Визначити максимальні значення повертаючої сили Fmax і кінетичної енергії Emax.
Відповідь: Fmax= 2 мН; Emax. = 50 мкДж.
116. Рух точки заданий рівняннями: 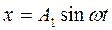 і
і 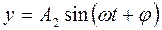 , де А 1 = 10 см; А2= 5 см; ω = 2с-1, j =p /4с. Знайти рівняння траєкторії і швидкість точки у момент часу t= 0,5 с.
, де А 1 = 10 см; А2= 5 см; ω = 2с-1, j =p /4с. Знайти рівняння траєкторії і швидкість точки у момент часу t= 0,5 с.
Відповідь: 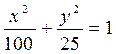 ; υ = 13,7 м/с.
; υ = 13,7 м/с.
117. Кулька масою m = 60 г коливається з періодом Т = 2 с. У початковий момент часу зміщення кульки складає х0 = 4 см і вона має енергію Е = 0,02 Дж. Записати рівняння простого гармонічного коливання кульки, закон зміни її прискорення і закон зміни повертальної сили з часом.
Відповідь: 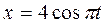 см;
см; 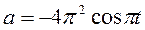 см/c2;
см/c2;  Н.
Н.
118. Рух тіла задано рівняннями  та
та  .
.
Знайти рівняння траєкторії та швидкість у момент часу t = 0,5 с, якщо А = 0,1 м, а В = 0,05 м, ω = 2 с-1;  с.
с.
Відповідь: 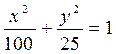 , υ = 13,7 м/с.
, υ = 13,7 м/с.
119. Тіло здійснює гармонічні коливання з частотою n = 15 Гц. Записати рівняння цього коливання, якщо початкова фаза  , а в момент максимального відхилення від положення рівноваги відновлювальна сила дорівнює F = 0,0005 Н.
, а в момент максимального відхилення від положення рівноваги відновлювальна сила дорівнює F = 0,0005 Н.
Відповідь:  .
.
120. Коливання матеріальної точки масою m = 10 - 3 кг протікає з амплітудою А = 10 – 2 см при частоті ν = 1 Гц. Визначити швидкість точки у момент часу, коли її зміщення від положення рівноваги складає х = 5∙10 – 3 м. Знайти амплітудне значення повертальної сили, що діє на точку та повну механічну енергію
Відповідь:  , F max = 40 мкН, Е = 20 мДж.
, F max = 40 мкН, Е = 20 мДж.
121. Вантаж масою 400 г здійснює коливання на пружині жорсткістю 250 Н/м. Амплітуда коливань 15 см. Знайти повну механічну енергію коливань і найбільшу швидкість руху вантажу.
Відповідь: Е = 2,80 Дж, υmax = 3,8 м/с.
122. Вантаж масою 1 кг на тонкій нитці завдовжки 1 м здійснює вільні коливання, максимальний кут відхилення нитки від вертикального положення 5o. Визначити силу пружності нитки під час проходження вантажем положення рівноваги.
Відповідь: F пр = 9,88 Н.
123. Визначити період Т простих гармонічних коливань диска радіусом R = 40 см навколо горизонтальної осі, що проходить через точку на ободі диска.
Відповідь: T = 1,55 с.
124. Дві пружини, коефіцієнт жорсткості яких k 1 = 2 Н/м і k 2 = 8 Н/м з'єднано один раз послідовно, другий раз паралельно.
У скільки разів будуть відрізнятися періоди коливань тягарця на таких пружинах?
Відповідь: у 2,5 рази.
125. Визначити період Т коливань математичного маятника, якщо модуль його максимальне відхилення А= 18 см і максимальна швидкість uтах =16 см/с.
Відповідь: T = 7,1 с.
126. Визначити частоту ν простих гармонічних коливань диска радіусом R = 20 см навколо горизонтальної осі, що проходить через середину радіуса диска перпендикулярно до його площини.
Відповідь: ν = 0,9 с-1.
127. Математичний маятник довжиною l = 1 м встановлений в ліфті. Ліфт підіймається з прискоренням а = 2,5 м/с2. Визначити період Т коливань маятника.
Відповідь: T = 1,8 с.
128. Вантаж, підвішений на пружині, коливається по вертикалі з амплітудою A = 0,08 м. Визначити жорсткість пружини, якщо максимальна кінетична енергія вантажу дорівнює EK = 0,8 Дж.
Відповідь: k = 250 Н/м.
129. На стрижні довжиною l = 30 см закріплені два однакових тягарці: один на середині стрижня, інший – на одному з його кінців. Стрижень з вантажами коливається навколо горизонтальної осі, що проходить через вільний кінець стрижня. Визначити приведену довжину L і період Т простих гармонічних коливань даного фізичного маятника. Масою стрижня знехтувати.
Відповідь: L = 25 см; T = 1 с.
130. Пружина має жорсткість k = 25 Н/м. Визначити, тіло якої маси потрібно підвісити на пружині, щоб за t = 60 с воно здійснювало N = 25 коливань.
Відповідь:m = 3,65 кг.
131. Математичний маятник, довжина нитки якого  1 м і радіус свинцевої кульки r = 0,02 м, здійснює гармонічні коливання з амплітудою A = 0,06 м. Визначити: швидкість кульки при її проходженні через положення рівноваги; максимальне значення повертальної сили. Густина свинцю ρ = 11300 кг/м3.
1 м і радіус свинцевої кульки r = 0,02 м, здійснює гармонічні коливання з амплітудою A = 0,06 м. Визначити: швидкість кульки при її проходженні через положення рівноваги; максимальне значення повертальної сили. Густина свинцю ρ = 11300 кг/м3.
Відповідь: υ = 0,186 м/с; F = 69,5 мН.
132. До спіральної пружини підвісили тягарець, внаслідок чого пружина розтягнулася на х = 9 см. Який буде період Т коливань тягарця, якщо його дещо відтягнути вниз і потім відпустити?
Відповідь: T = 0,6 с.
133. Автомобіль рухається по нерівній дорозі з горбами, відстань між якими 0,7 м. З якою швидкістю має рухатися автомобіль, щоб кулька, підвішена в салоні автомобіля на нерозтяжній нитці довжиною 30 см, коливалась з найбільшою амплітудою.
Відповідь:υ = 0,63 м/с.
134. Гиря, підвішена до пружини, коливається по вертикалі з амплітудою А = 4 см. Визначити повну енергію Е коливань гирі, якщо жорсткість пружини дорівнює k =1 кН/м.
Відповідь: E = 0,8 Дж.
135. Тонкий обруч, повішений на цвях, вбитий горизонтально в стіну, коливається в площині, паралельній стіні. Радіус обруча дорівнює R = 30 см. Обчислити період Т коливань обруча.
Відповідь: T = 1,55 с.
136. Куля масою m = 0,5 кг підвішена на пружині, жорсткість якої k = 32 Н/м, і здійснює затухаючі коливання. Визначити їх період у двох випадках: 1) коли за час, протягом якого відбулося N 1 = 88 коливань, амплітуда зменшилася в n 1 = 2 рази; 2) коли за час двох коливань (N 2 = 2) амплітуда зменшилася в n2 = 20 разів.
Відповідь: T1 = 0,78 с; T2 = 0,81 с.
137. При спостереженні затухаючих коливань виявилося, що для двох послідовних коливань амплітуда другого менша за амплітуду першого на 0,6 см. Період затухаючих коливань T = 0,5 с. Визначити: коефіцієнт затухання і частоту затухаючих коливань.
Відповідь: b = 1,83 с-1; ν = 2,02 Гц.
138. Період власних коливань пружинного маятника дорівнює T1 = 0,55 с. У в'язкому середовищі період маятника становить T2 = 0,56 с. Визначити резонансну частоту коливань.
Відповідь: ν рез = 1,75 Гц.
139. Тіло масою т = 100 г, здійснюючи затухаючі коливання, за τ = 1 хв втратило 40% своїй енергії. Визначити коефіцієнт опору r
Відповідь: r = 8,51×10-4 кг/с.
140. За час, протягом якого система здійснює N = 50 повнихколивань, амплітуда зменшується в 2 рази. Визначити добротність Q системи.
Відповідь: Q = 227.
141. Частота вільних коливань деякої системи ω = 65 рад/с, а її добротність Q = 2. Визначити власну частоту коливань цієї системи
Відповідь: ω = 67 рад/с.
142. Частота затухаючих коливань в коливальному контурі з добротністю Q = 2500 дорівнює ν = 550 кГц.
Визначити час, за який амплітуда сили струму в цьому контурі зменшиться в 4 рази.
Відповідь: τ = 2 мс.
143. Власна частота коливань деякої системи складає ν0 = 500 Гц. Визначити частоту  затухаючих коливань цієї системи, якщо резонансна частота ν рез = 499 Гц
затухаючих коливань цієї системи, якщо резонансна частота ν рез = 499 Гц
Відповідь: ν = 499,5 Гц.
144. Визначити період Т затухаючих коливань, якщо періодвласних коливань системи дорівнює Т0 = 1 с, логарифмічний декремент коливань l= 0,628.
Відповідь: Т= 1,005 c.
145. Знайти число N повних коливань системи, протягом яких енергія системи зменшилася в n = 2 рази. Логарифмічний декремент коливань l = 0,01.
Відповідь: N= 35.
146. Коливальна система здійснює затухаючі коливання з частотою ν = 1000 Гц. Визначити частоту ν0 власних коливань, якщо резонансна частота ν рез = 998 Гц.
Відповідь: ν0 = 1002 Гц.
147. Амплітуда затухаючих коливань маятника за час t1 = 5 хв зменшилася вдвічі. За який час t 2 від початкового моменту амплітуда зменшиться у вісім разів?
Відповідь: t2 = 15 хв.
148. Логарифмічний декремент коливань маятника дорівнює l = 0,003. Визначити число N повних коливань, які повинен здійснити маятник, щоб амплітуда зменшилася вдвічі.
Відповідь: N = 230.
149. Тіло масою т = 5 г здійснює затухаючі коливання. За час t = 50 с воно втратило 60% своєї енергії. Визначити коефіцієнт опору r.
Відповідь: r = 9,16·10-5 кг/с.
150. Амплітуда затухаючих коливань маятника за  120 с зменшилась в 2 рази. Визначити коефіцієнт затухання.
120 с зменшилась в 2 рази. Визначити коефіцієнт затухання.
Відповідь: b = 5,78·10-3 с-1.
151. Складаються два гармонічних коливання одного напрямку з однаковими періодами Т1 = Т2 = 1,5 с і амплітудами А1 = А2 = 2 см. Початкові фази коливань φ 1 = π/2, φ 2 = π//3.Визначити амплітуду А і початкову фазу φ результуючого коливання. Знайти його рівняння і побудувати з дотриманням масштабу векторну діаграму додавання амплітуд.
Відповідь: A = 3,86 см; φ = 0,417 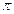 рад; ω = 4,19 с-1;
рад; ω = 4,19 с-1;  .
.
152. Два однаково напрямлені гармонічні коливання одного періоду з амплітудами А1 = 10 см і А2 = 6см складаються в одне коливання з амплітудою А = 14 см. Знайти різницю фаз Δφ коливань.
Відповідь:  рад.
рад.
153. Точка бере участь у двох однаково напрямлених коливаннях: х1 = А1 sin 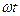 і х2 = А2 cos
і х2 = А2 cos 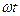 , де А1 = 1 см; А2 = 2 cм; ω = 1 с-1. Визначити амплітуду А результуючого коливання, його частоту ν і початкову фазу φ. Знайти рівняння цього руху.
, де А1 = 1 см; А2 = 2 cм; ω = 1 с-1. Визначити амплітуду А результуючого коливання, його частоту ν і початкову фазу φ. Знайти рівняння цього руху.
Відповідь: A = 2,24 см; ν = 0,16 Гц; φ = 0,35π;  см.
см.
154. Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, рівняння яких мають вигляд х =А1 sin  1 t і y = А2 соs
1 t і y = А2 соs  2t, де А1 = 8 см, А2 = 4 см; ω 1 = ω2 = 2 с-1. Написати рівняння траєкторії і побудувати її. Показати напрям руху точки.
2t, де А1 = 8 см, А2 = 4 см; ω 1 = ω2 = 2 с-1. Написати рівняння траєкторії і побудувати її. Показати напрям руху точки.
Відповідь:  ; це – еліпс з напівосями 8 см та 4 см, рух відбувається за годинниковою стрілкою, починаючи з точки (0,4) см.
; це – еліпс з напівосями 8 см та 4 см, рух відбувається за годинниковою стрілкою, починаючи з точки (0,4) см.
155. Складаються два взаємно перпендикулярні коливання, що описуються рівняннями х = А1 sin  t і y = =А2 cos
t і y = =А2 cos  (t+
(t+ 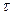 ), де А1 = 2 см; А2 = 1 см; ω =
), де А1 = 2 см; А2 = 1 см; ω =  с-1, τ = 0,5 с. Знайти рівняння траєкторії і побудувати її, вказати напрям руху точки.
с-1, τ = 0,5 с. Знайти рівняння траєкторії і побудувати її, вказати напрям руху точки.
Відповідь: 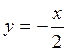 .
.
156. Точка приймає участь одночасно у двох гармонічних коливаннях, що відбуваються у двох взаємно перпендикулярних напрямках. Рівняння цих коливань мають вигляд х = А1 сos  t і y = А2 cos
t і y = А2 cos  (t+
(t+ 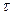 ), де А1= 4 см; А2 = 8 см; ω = πс-1, τ = 1 с. Знайти рівняння траєкторії точки і побудувати графік її руху.
), де А1= 4 см; А2 = 8 см; ω = πс-1, τ = 1 с. Знайти рівняння траєкторії точки і побудувати графік її руху.
Відповідь: y = - 2 x.
157. Матеріальна точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, що описуються рівняннями х = А1 cos  t і y = -А2 cos 2
t і y = -А2 cos 2  t, де А 1 = 2 см; А2 = = 1 см. Знайти рівняння траєкторії руху і побудувати її.
t, де А 1 = 2 см; А2 = = 1 см. Знайти рівняння траєкторії руху і побудувати її.
Відповідь: 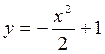 .
.
158. Точка бере участь одночасно в двох взаємно перпендикулярних коливаннях, що описуються рівняннями х = А1 cos  t і y = А2 sin 0,5
t і y = А2 sin 0,5  t, де А1= 2 см; А2 = 3 см. Знайти рівняння траєкторії точки і побудувати її, вказати напрямок руху.
t, де А1= 2 см; А2 = 3 см. Знайти рівняння траєкторії точки і побудувати її, вказати напрямок руху.
Відповідь: 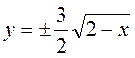 .
.
Дата добавления: 2015-07-25; просмотров: 245 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тестовое задание | | | Универсальность переживаний. |