Постановка задачи размещения

В общем виде задача размещения заключается в определении оптимального в смысле некоторого критерия положения элементов и связей между ними в монтажном пространстве типовой конструкции. При этом должны быть удовлетворены заданные конструктивно-технологические ограничения. В такой постановке задачу размещения можно сформулировать как целочисленное программирование, однако из-за большой размерности ее практическая реализация нецелесообразна. Задачу размещения условно разбивают на две: размещение конструктивных элементов и трассировка связей между ними.

При таком подходе задача размещения сводится к нахождению оптимального положения элементов и внешних контактов в монтажной области типовой конструкции. В ряде алгоритмов размещение элементов выполняется без учета их связей с внешними выводами, поэтому элементы, имеющие связи с внешними выводами, могут оказаться на значительном удалении от них, что затруднит последующую трассировку соединений.

Исходные данные для задачи размещения: схема соединения элементов, метрические параметры и топологические свойства монтажного пространства. Для типовых конструкций ЭВМ, начиная с субблока, характерно регулярное монтажное пространство. Тогда задачу размещения можно сформулировать следующим образом. Имеются множество конструктивных элементов E={e_i / i=1, N}и множество соединяющих их цепей Q={q_k / k=1, K}. Монтажное пространство определено множеством фиксированных позиций для установки элементов T={t_j / j=1, M}, причем M ≥ N. Найти такое отображение множества Е в множество Т, при котором достигается экстремум целевой функции F.

Главная цель размещения – создание наилучших условий для трассировки. Из-за условности разделения задач размещения и трассировки трудно установить для задачи размещения такой критерий оптимизации, который в достаточной мере удовлетворял бы требованиям трассировки. В настоящее время используют критерии: минимум суммарной длины всех соединений или длины самой длинной связи; минимум числа пересечений связей при произвольной их конфигурации; максимум числа цепей с возможно более простой конфигурацией; максимально близкое расположение модулей, имеющих наибольшее количество связей между собой. Указанные критерии лишь качественно способствуют решению главной задачи размещения. Наиболее распространен критерий минимума суммарной длины соединений, так как при его оптимизации косвенно минимизируются длина связей и число их пересечений, снижаются искажения сигналов.

Для N элементов, которые могут быть установлены в M позиций, существует множество размещений A={a_l / l=1, L}, их количество

В связи с этим поиск оптимального варианта размещения полным перебором нецелесообразен уже при N=15…20. В дальнейшем будем полагать, что M=N. Если число элементов меньше числа позиций, можно ввести M – N фиктивных элементов.

Алгоритмы размещения можно свести в основные группы: алгоритмы решения задач математического программирования, являющихся моделями задачи размещения; последовательные алгоритмы; итерационные алгоритмы; алгоритмы, использующие непрерывно-дискретные методы оптимизации.

Рассмотрим постановку задачи размещения как задачи квадратичного назначения при использовании критерия минимума суммарной длины соединений. В качестве схемы математической модели будем использовать взвешенный неориентированный мультиграф, в котором элементы схемы сопоставлены с вершинами, а каждая цепь представляется полным подграфом. Связность элементов схемы задается матрицей соединений R, элемент r_i,j которой отражает взвешенную связанность вершин и :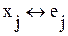

,

где 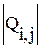– число цепей, в которые входят одновременно элементы e_iи e_j; 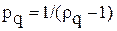– вес q-й связи; r_q – количество элементов, соединяемых

q-й цепью.

Будем считать, что соединения исходят из геометрических центров конструктивных элементов, метрика – ортогональная, расстояние между соседними позициями по горизонтали и вертикали одинаковое. Тогда математической моделью монтажного пространства будет граф решетки G _r, а расстояния между позициями установки элементов будут определены матрицей расстояний графа D _r.

Внешние выводы сопоставим с элементом е₀. Соединения с ним элементов из множества Е учтем вектором столбцов взвешенных связей H={h_i / I=1, N}. Монтажная область внешних выводов обычно фиксирована на периферии типовой конструкции, т.е. расположение контактных площадок задано. Контактные площадки, кроме выводов питания и земли, инвариантны. Поэтому расстояние от элемента е_i до внешних выводов можно приближенно определять как расстояние от вертикального (горизонтального) ряда, в котором установлен этот элемент, до контактной группы.

Для некоторого размещения суммарная взвешенная длина соединений

,

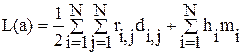где d_i,j – элемент матрицы D _r, определяет расстояние между позициями установки конструктивных элементов e_iи e_j; m_i – номер вертикального ряда, в котором расположен элемент e_i.

Теперь задача заключается в минимизации L(a) на множестве размещений А. Это один из вариантов задачи квадратичного назначения, точное решение которой можно найти, например, методом ветвей и границ. Алгоритмы, реализующие этот метод, можно использовать на практике при N=15…20.

Дата добавления: 2015-07-25