Схема 2

Схема 1

Из (1) при :

2) При : Получаем схему замещения цепи:

Схема 2

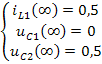По уравнениям (1) приравняв их левую часть к 0 получаем: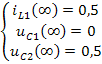

Находим характеристический полином:

Корни характеристического полинома:

Корни характеристического полинома совпали с полюсами передаточной функции.

5. Определение переходной и импульсной характеристик:

1. Аналитический метод:

Входное воздействие , начальные условия – нулевые. Рассчитаем по уравнениям состояния напряжение , а затем, зная его, найдём переходную характеристику.

Общий вид решения:

Вынужденную составляющую решения находим из системы (1), приравняв левую часть к нулю:

Свободная составляющая решения:

Находим постоянные интегрирования :

Начальное значение напряжения:

Начальное значение первой производной находим по третьему уравнению системы (1):

Начальное значение второй производной находим, продифференцировав третье уравнение системы (1):

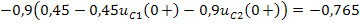
Получаем систему для определения постоянных интегрирования :

Решая систему, получаем:

Напряжение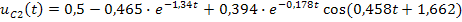

Реакцию найдём по уравнению связи:

Значения и , полученные по этому выражению и по схемам замещения цепи (см. прошлый пункт, схема 1 и схема 2) совпадают.

Находим импульсную характеристику :

Графики переходной и импульсной характеристик:

2) Численный метод:

Уравнения состояния в матричной форме:

Входное воздействие , начальные условия – нулевые.

Для нахождения переходной характеристики используем явную форму алгоритма Эйлера:

Шаг расчёта: ;
; Выбираем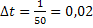

Оценка точности численного расчёта:

Для переходной характеристики:

1)

2)

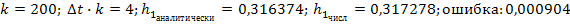
3)

Точность численного метода высока. Точность численного метода повышается с уменьшением .

6. Вычисление реакции цепи при воздействии

Дата добавления: 2015-07-25