
|
Читайте также: |
Выпускается автомобиль УАЗ-3160 с 1997 г. Этот джип, отвечает всем современным требованиям, предъявляемым к автомобилям такого класса.
Грузопассажирский с цельнометаллическим пятидверным кузовом, двигатель мод. УМЗ-420 с рабочим объёмом 2,445 л. и впрыском топлива, мощностю 65,5 кВт. [2, с.17]
База, мм:  ; [2, с.5]
; [2, с.5]
Габариты:
Длина, мм:  ;
;
Ширина, мм:  ;
;
Высота, мм:  ;
;
Колея, мм:  ;
;
Масса перевозимого груза, включая водителя и пассажиров, кг:  ; [2, с.16]
; [2, с.16]
Число мест для сидения (без откидных):  ;
;
Масса снаряжённого автомобиля, кг:  ;
;
Полная масса:  ;
;
Максимальная скорость, км/ч: 130;
Подвеска комбинированная;
передняя – пружинная со стабилизаторами поперечной установки;
задняя – на продольных полуэллиптических рессорах;
Шины 225/75R16; [2, с.188]
Распределение масс автомобиля по осям: [10, 3-4]
Передняя ось задняя ось:
Снаряжённое состояние, кг: 946, 984;
Полная масса, кг: 1088, 1442;
Расчёт подвески.
1. Снаряжённая масса автомобиля включает себя: заполненную и заряженную аккумуляторную батарею, смазочные средства, тормозную жидкость, охлаждающую жидкость, комплект инструмента стандартный, заполненный, по крайней мере на 90%, топливный бак, знаки аварийной остановки, медицинскую аптечку, огнетушитель. [4, с.22]
Масса водителя учитывается для транспортных средств, кроме легковых и грузопассажирских. В данном случае для автомобиля УАЗ-3160 масса водителя в снаряжённую массу не входит.
2. Грузоподъёмность (общая перевозимая масса).
 кг [4, с.24],
кг [4, с.24],
Где 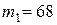 – масса одного человека (европейские данные), кг;
– масса одного человека (европейские данные), кг;
 – масса груза в багажнике, кг;
– масса груза в багажнике, кг;
 – количество человек.
– количество человек.
Масса одного перевозимого человека взята по международному стандарту ИСО ДИС-2416 «Дорожный транспорт, распределение нагрузки в грузопассажирских автомобилях». Представляет из себя среднюю величину массы одного пассажира.
3. Определение осевых нагрузок на дорогу.
Багажник – грузовой отсек – расположен сзади.
Таблица 1.
| Распределение снаряжённой массы по осям | ||
| На переднюю ось | 946 кг | 9270,8 Н |
| На заднюю ось | 984 кг | 9643,2 Н |
| Распределение полной массы по осям | ||
| На переднюю ось | 1088 кг | 10662,4 Н |
| На заднюю ось | 1442 кг | 14131,6 Н |
4. Неподрессорные массы включают в себя: массы колёс и деталей, связанных с колёсами через подшипники, а также часть масс деталей которые соединяют колесо с кузовом, поперечной подвеской или рамой: полуоси, рычаги, пружины, амортизаторы и детали крепления. Принимает  кг.
кг.
5. Упругая характеристика подвески в нагруженном состоянии.
5.1. Для удовлетворения требований плавности хода должна обеспечивать определённый закон изменения вертикальных реакций на колесо  , в зависимости от прогиба – зависимость эта называется упругой характеристикой подвески (рис. 2). [5, с.25]
, в зависимости от прогиба – зависимость эта называется упругой характеристикой подвески (рис. 2). [5, с.25]

Рис. 1. Распределение реакций на переднюю т заднюю оси со стороны дороги.
5.2. В некотором диапазоне изменения нагрузок, близком к статической  , характеристика подвески должна обеспечивать оптимальную частоту колебаний: 0,8–1,2 Гц, что соответствует уровню колебаний человека при ходьбе. [6, с.253]
, характеристика подвески должна обеспечивать оптимальную частоту колебаний: 0,8–1,2 Гц, что соответствует уровню колебаний человека при ходьбе. [6, с.253]
5.3. Ход колеса – вертикальное перемещение  , относительно несущей системы. Перемещение колеса вверх называют ходом сжатия, вниз – ходом отдачи. Максимальный ход сжатия состоит из двух частей: статического
, относительно несущей системы. Перемещение колеса вверх называют ходом сжатия, вниз – ходом отдачи. Максимальный ход сжатия состоит из двух частей: статического  и динамического
и динамического  ходов.
ходов.
Статический ход – это перемещение колеса из положения, соответствующего полностью разгруженному состоянию другого элемента, в положение, занимаемое колесом при воздействии на него номинальной статической нормальной реакции дороги.
Динамический ход – это перемещение колеса из статического положения в верхнее предельное положение при деформированном ограничителе хода сжатия – буфере.
Коэффициент динамичности  подвески – отношение наибольшей нормальной реакции дороги на колесо к статической реакции. Его можно принять равным
подвески – отношение наибольшей нормальной реакции дороги на колесо к статической реакции. Его можно принять равным  . [6, с.253]
. [6, с.253]
Жёсткость подвески  – это первая производная от нагрузки по ходу
– это первая производная от нагрузки по ходу  колеса. При линейной характеристике, жёсткость постоянна и равна тангенсу угла наклона характеристики к оси перемещения.
колеса. При линейной характеристике, жёсткость постоянна и равна тангенсу угла наклона характеристики к оси перемещения.
Жёсткость упругого элемента – зависимость между нагрузкой 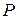 на упругий элемент и его деформацией (прогибом
на упругий элемент и его деформацией (прогибом  ):
):
 ; [6, с.253]
; [6, с.253]
На стадии проектирования подвески задаются значениями  и по графику [6, с.254, рис. 169] определяют необходимые статические ходы колёс, при движении без учёта галокопирования.
и по графику [6, с.254, рис. 169] определяют необходимые статические ходы колёс, при движении без учёта галокопирования.
Таблица 2.
| Зависимость собственной частоты колебаний подрессорной массы от статического хода | 
| Гц | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 |

| м | 0,21 | 0,15 | 0,12 | 0,08 | 0,04 |
Где  – частота собственных колебаний подрессорной массы, Гц. Является одной из основных характеристик подвески.
– частота собственных колебаний подрессорной массы, Гц. Является одной из основных характеристик подвески.
Для обеспечения необходимой плавности хода автомобиля частота собственных колебаний кузова легковых автомобилей должна быть в пределах 1-1,5 Гц. Принимаем  Гц. Тогда
Гц. Тогда  мм. [6, с.254]
мм. [6, с.254]
5.4. Усилие от полной массы автомобиля в пружине подвески статическое:
 кН.;
кН.;
Где  – реакция от полной массы на колесо от дороги, Н;
– реакция от полной массы на колесо от дороги, Н;
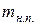 –неподрессорная масса задней оси, кг.
–неподрессорная масса задней оси, кг.
5.5. Построение упругой характеристики.
Построение упругой характеристики производим с допущениями: пренебрегаем трением в подвеске, массой неподрессорных частей, считаем упругую характеристику прямолинейной, прогиб упругого элемента равен ходу колеса. [6, с.256, с.262]
По формуле  [7, с.235] определяем текущее значение вертикальной нагрузки при начальных условиях
[7, с.235] определяем текущее значение вертикальной нагрузки при начальных условиях  , деформацией
, деформацией 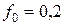 м,
м, 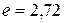 основание натурального логарифма.
основание натурального логарифма.
Статический прогиб:  м;
м;
Динамический прогиб:  м.
м.
При  , находим
, находим  :
:
 кН.
кН.
Проведём расчеты.
Полученные данные занесём в таблицу 3.
Таблица 3.
| Расчёт усилия на упругий элемент в зависимости от деформации. | |||
 , м , м
| 
| 
| 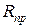 , кН , кН
|
| 0,05 | -0,75 | 0,46 | 2,85 |
| 0,10 | -0,50 | 0,606 | 3,76 |
| 0,15 | -0,25 | 0,779 | 4,83 |
| 0,20 | 1,0 | 6,20 | |
| 0,25 | 0,25 | 1,28 | 7,94 |
| 0,30 | 0,50 | 1,65 | 10,23 |
| 0,33 | 1,65 | 1,9 | 11,78 |
По данным таблицы 3 строим упругую характеристику.
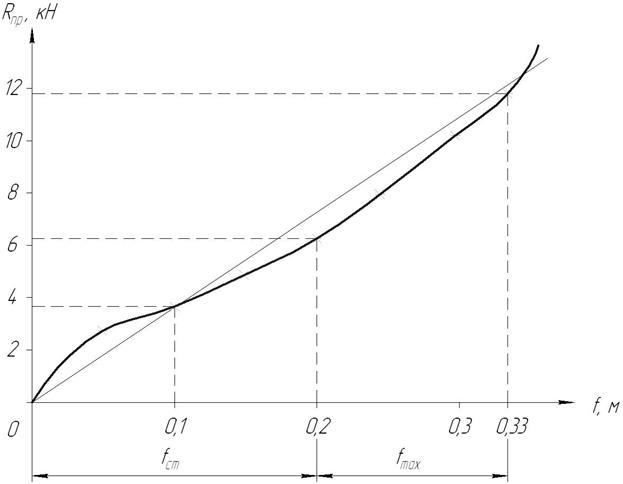
Рис. 2. Упругая характеристика подвески.
Полученная характеристика соответствует полностью желаемой характеристике, изменяющейся по закону показательной функции. 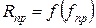 . [7, с.235]
. [7, с.235]
6. Расчёт упругого элемента.
В качестве упругого элемента применяем цилиндрическую винтовую пружину сжатия, изготовленную из проволоки круглого поперечного сечения.
В поперечном сечении винта возникают только два касательных напряжения. Для их определения введём допущения:
6.1. Касательные напряжения, связанные с наличием крутящего момента определяются так же, как для прямого бруска круглого сечения. Эпюра этих напряжений для точек горизонтального диаметра дана на рис. 3:

Рис. 3. Эпюра касательных напряжений.
 МПа
МПа
Где 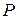 – усилие сжатия пружины,
– усилие сжатия пружины,  кН (таблица 3);
кН (таблица 3);
 – средний диаметр витка пружины, м;
– средний диаметр витка пружины, м;
 – диаметр проволоки, м;
– диаметр проволоки, м;
Пружина:  мм;
мм;
 мм;
мм;
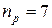 – количество рабочих витков;
– количество рабочих витков;
Условие эксплуатации по допустимому касательному напряжению от крутящего момента соблюдается, при материале пружины сталь 65Г  МПа [8, с.149]:
МПа [8, с.149]:
 МПа <
МПа <  ;
;
6.2. Касательные напряжения, связанные с наличием поперечной силы, распределяется по сечению равномерно. Эпюра этих напряжений дана на рис. 4.

Рис. 4. Эпюра касательных напряжений от поперечной силы.
 МПа;
МПа;
6.3. Общее значение касательного напряжения.[8, с.147]
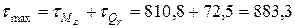 МПа;
МПа;
6.4. Проверка правильности выбора параметров пружины.[8, с.151]
 м;
м;
Где  – поправочный коэффициент, зависящий от индекса и прочности пружины.
– поправочный коэффициент, зависящий от индекса и прочности пружины.
 – отношение среднего диаметра пружины к диаметру проволоки;
– отношение среднего диаметра пружины к диаметру проволоки;
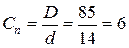 ;
;
Соотношения 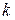 и
и  принимаем по [8, с.149].
принимаем по [8, с.149].
 ;
;
 ;
;
С учётом того, что  МПа, принимаем
МПа, принимаем  мм.
мм.
6.5. Определяем число витков, учитывая что приращению нагрузки  кН, соответствует осадка
кН, соответствует осадка  мм, где
мм, где  – максимальное значение нагрузки, кН;
– максимальное значение нагрузки, кН;  – нагрузка в снаряжённом состоянии, кН:
– нагрузка в снаряжённом состоянии, кН:
 ;
;
Где  – модуль сдвига, МПа;
– модуль сдвига, МПа;
Полное число витков принимается на 1,5-2 витка больше.
 , принимаем 8,5 витков.
, принимаем 8,5 витков.
Нужно стремиться, чтобы число витков заканчивалось на 0,5, при этом крайние витки будут развёрнуты в противоположные стороны.
6.6. Высота пружины, полностью сжатой под действием максимальной нагрузки:
 м;
м;
Где  – количество рабочих витков;
– количество рабочих витков;
 – учитывает прижатые концевые витки;
– учитывает прижатые концевые витки;
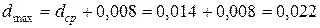 м
м
6.7. Относительная упругость, как функция гибкости пружины:
 ;
;
 , т.е. у пружины, в результате расчётов, гарантировано отсутствие продольного изгиба, дополнительный элемент, предотвращающий изгиб пружины в продольном направлении не потребуется.
, т.е. у пружины, в результате расчётов, гарантировано отсутствие продольного изгиба, дополнительный элемент, предотвращающий изгиб пружины в продольном направлении не потребуется.
7. Расчёт направляющего устройства.
Нижняя продольная штанга.
7.1. Расчёт при действии максимальной силы тяги (при разгоне).
7.1.1 Обычно при расчетах принимают коэффициент сцепления  . [7, с.217]
. [7, с.217]
Максимально возможная сила тяги на колесе:
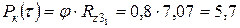 кН,
кН,
Где  – коэффициент сцепления колеса с дорогой;
– коэффициент сцепления колеса с дорогой;
 – нормальная реакция на колесо от дороги.
– нормальная реакция на колесо от дороги.
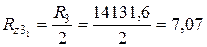 кН
кН
|

Рис. 5. Схема расстановки сил при разгоне.
7.1.2 Напряжение смятия (сжатия) от силы 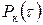 ;
;
 МПа <
МПа <  МПа,
МПа,
Где  – площадь поперечного сечения трубчатой штанги, м2;
– площадь поперечного сечения трубчатой штанги, м2;
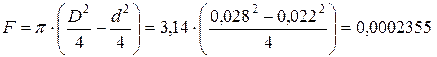 м2;
м2;
Труба 28х3 – 20 ГОСТ 8734-58
 мм,
мм,  мм; [9, с.588]
мм; [9, с.588]

Рис. 6. Сечение штанги.
Условие эксплуатации соблюдается.
7.2. Расчёт штанги при действии максимальной прижимной силы.
7.2.1. Сила тормозная.
Определяется по формуле:
 Н;
Н;
Где  – реакция на колесо, с учётом перераспределения нагрузки между мостами при торможении.
– реакция на колесо, с учётом перераспределения нагрузки между мостами при торможении.
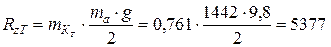 Н;
Н;
 – коэффициент перераспределения;
– коэффициент перераспределения;
 – масса автомобиля, приходящаяся на ведущую заднюю ось, кг;
– масса автомобиля, приходящаяся на ведущую заднюю ось, кг;
 – ускорение земного притяжения, м/с2;
– ускорение земного притяжения, м/с2;
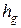 – высота центра масс, м (рис. 1);
– высота центра масс, м (рис. 1);
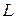 – база автомобиля;
– база автомобиля;
 .
.
7.2.2. Напряжение растяжения штанги.
 МПа <
МПа <  МПа.
МПа.
7.3. Условие эксплуатации по допускаемым напряжениям сжатия и растяжения профильной штанги соблюдается.
8. Расчёт балки заднего моста.
8.1. Предварительно размеры поперечного сечения сварной балки или кожуха полуоси в месте крепления пружины при компоновке моста можно определять по моменту сопротивления изгибу (см3), определяемому по формулам:
 см3; [7, с.216]
см3; [7, с.216]
 – масса подрессорной части автомобиля, приходящаяся на задний мост, кг
– масса подрессорной части автомобиля, приходящаяся на задний мост, кг
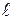 – расстояние от центральной плоскости колеса до середины пружины подвески, см;
– расстояние от центральной плоскости колеса до середины пружины подвески, см;
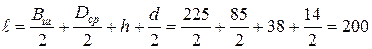 мм; [2, с.178]
мм; [2, с.178]
Где  – ширина шины, мм;
– ширина шины, мм;
 – средний диаметр пружины, мм;
– средний диаметр пружины, мм;
 – диаметр проволоки пружины, мм;
– диаметр проволоки пружины, мм;
 – зазор между колесом и пружиной, мм.
– зазор между колесом и пружиной, мм.

Рис. 7. Пояснительная схема к расчёту.
8.2. Напряжения при действии максимальной силы тяги или максимальной тормозной силы.
Принимаем коэффициент сцепления колеса с дорогой  [7, с.217]
[7, с.217]
Максимально возможная сила тяги (1) или тормозная сила (2) на колесе:
1).  Н; [7, с.217]
Н; [7, с.217]
2).  Н;
Н;
Где  – реакция на колесо, вычисленная с учётом перераспределения нагрузки между мостами при разгоне (1) или торможении (2).
– реакция на колесо, вычисленная с учётом перераспределения нагрузки между мостами при разгоне (1) или торможении (2).
1).  Н; [7, с.217]
Н; [7, с.217]
2).  Н,
Н,
 – доля полной массы автомобиля, приходящаяся на колёса заднего моста, кг;
– доля полной массы автомобиля, приходящаяся на колёса заднего моста, кг;
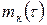 – коэффициент перераспределения нагрузки на колесе:
– коэффициент перераспределения нагрузки на колесе:
– при разгоне:  ; [7, с.217]
; [7, с.217]
– при торможении: 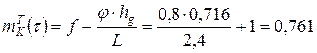 ;
;
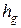 – высота расположения центра масс, м;
– высота расположения центра масс, м;
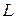 – база автомобиля, м.
– база автомобиля, м.
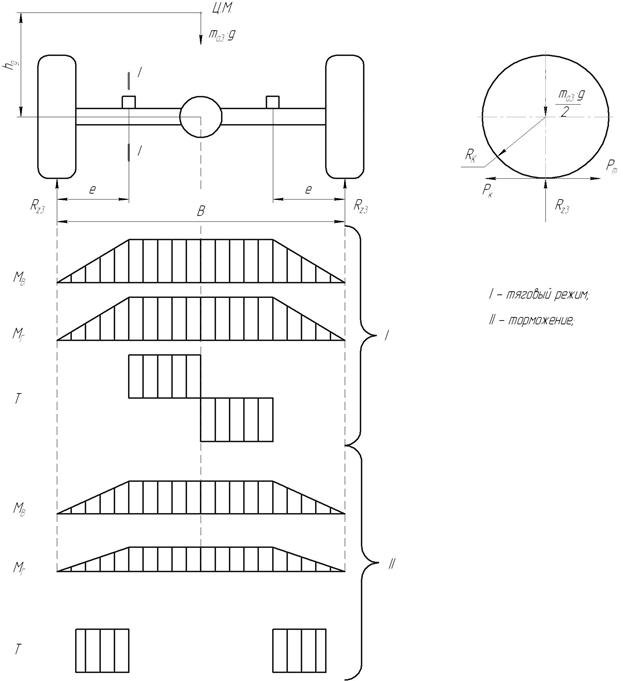
Рис. 8. Схема сил, действующих на ведущий мост при максимальной тяги и торможении и эпюры изгибающих моментов.
 м;
м;
 – диаметр посадочный, дюйм;
– диаметр посадочный, дюйм;
 – ширина шины.
– ширина шины.
Изгибающие моменты, создаваемые  в вертикальной плоскости и
в вертикальной плоскости и  в горизонтальной плоскости, достигают максимальных значений в сечении I-I в месте крепления пружины и продольной штанги.
в горизонтальной плоскости, достигают максимальных значений в сечении I-I в месте крепления пружины и продольной штанги.
Если принять, что на балку действует сила, равная вертикальной реакции в точке контакта колеса с опорной поверхностью, то:
1).  Н·м; [7, с.217]
Н·м; [7, с.217]
2).  Н·м;
Н·м;
1). 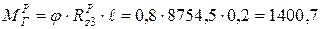 Н·м;
Н·м;
2).  Н·м;
Н·м;
Где 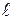 – расстояние от центра колеса до центра пружины.
– расстояние от центра колеса до центра пружины.
Реактивный крутящий момент, создаваемый силой тяги, действует на балку на участке от оси симметрии главной передачи до места крепления штанг продольных, а реактивный тормозной момент – на участке от фланца крепления суппорта тормозного механизма до места крепления пружины:
1).  Н·м;
Н·м;
2).  Н·м;
Н·м;
Где  – колея автомобиля, м;
– колея автомобиля, м;
 – радиус качения колеса
– радиус качения колеса
При круглом сечении балки (трубчатой) суммарный момент в опасном сечении согласно теории наибольших касательных напряжений: [7, с.218]
1).  Н·м;
Н·м;
2).  Н·м;
Н·м;
1). 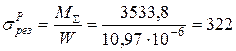 МПа <
МПа <  МПа;
МПа;
2).  МПа <
МПа <  МПа;
МПа;
Где  – осевой момент сопротивления, м3.
– осевой момент сопротивления, м3.
8.3. Напряжения, возникающие при заносе.
Вертикальные и горизонтальные реакции, действующие в точке контакта с опорной поверхностью для случая скольжения автомобиля влево, определяют по формулам: [7, с.218]
 Н;
Н;
 Н;
Н;
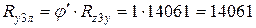 Н;
Н;
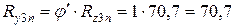 Н.
Н.

Рис. 9. Схема сил, действующих на ведущий мост при заносе автомобиля, и эпюры изгибающих моментов.
При боковом скольжении коэффициент сцепления колеса с дорогой принимают  .
.
В случае скольжения автомобиля влево изгибающий момент на левой стороне балки достигает максимального значения в сечении I-I, соответственно центральной плоскости колеса, а изгибающий момент правой балки – в сечении II-II – месте крепления пружины.
 Н·м;
Н·м;
 Н·м;
Н·м;
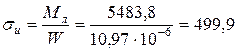 МПа <
МПа <  МПа.
МПа.
8.4. При переезде препятствия.
Напряжение изгиба в месте крепления пружины определяют по формуле: [7, с.219]
 МПа <
МПа <  МПа;
МПа;
Где  – момент в вертикальной плоскости при максимальном значении вертикальной реакции на колесо.
– момент в вертикальной плоскости при максимальном значении вертикальной реакции на колесо.
 Н;
Н;
Где  – коэффициент динамичности;
– коэффициент динамичности;
 Н·м.
Н·м.
Список литературы.
1. Методические указания.
2. Э. Н. Орлов и др. «Автомобили УАЗ «Техническое обслуживание и ремонт», – М., Транспорт, 2002 г., 336 с.
3. Краткий автомобильный справочник, – НИИАТ, М. Трансконсалтинг, 1994 г., 779 с.
4. Й. Раймпель «Шасси автомобиля», – М., Машиностроение, 1983 г., 356 с.
5. В. В. Осепчугов и др. «Автомобиль, анализ конструкции, элементы расчёта», – М., Машиностроение, 1989 г., 304 с.
6. Г. А. Гаспарянц, «Конструкция, основы теории и расчёта автомобиля», М., Машиностроение, 1978 г., 351 с.
7. П. П. Лукин и др. «Конструирование и расчёт автомобилей», – М., Машиностроение, 1984, 376 с.
8. Г. М. Ицкевич, «Сопротивление материалов», – М., Высшая школа, 1968 г., 383 с.
9. В. И. Анурьев «Справочник конструктора-машиностроителя», – М., Машиностроение, 1968 г., 688 с.
10. Автомобиль УАЗ-3160 и его модификации, Эксплуатация и техническое обслуживание.
11. Г. С. Писаренко и др. «Справочник по сопротивлению материалов», Киев, Наукова думка, – 1975 г., 704 с.
Дата добавления: 2015-07-25; просмотров: 87 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| АНАЛИЗ КОНСТРУКЦИИ ПОДВЕСКИ | | | Процедура исследования |