Решение. Составим расширенную матрицу и выполним над ней элементарные преобразования

Составим расширенную матрицу и выполним над ней элементарные преобразования, указанные в методе Гаусса.

Метод Гаусса решения системы (1) состоит в следующем:

Разделим все члены первого уравнения на , а затем, умножив полученное уравнение на , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное будет исключено, и получится система вида:

(2)

Теперь разделим второе уравнение системы (2) на , умножим полученное уравнение на и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное будет исключено и получится система треугольного вида:

(3)

Из последнего уравнения системы (3) находим . Подставляя найденное во второе уравнение, находим . Наконец, подставляя найденное значение в первое уравнение, находим .

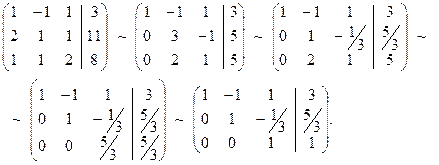
Последней матрице соответствует ступенчатая система уравнений:

,

равносильная исходной.

Из этой системы последовательно находим:

Таким образом: .

Выполним проверку, подставив найденные значения в исходную систему:

,

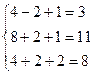Каждое уравнение системы обращается в верное равенство, следовательно, 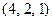– единственное решение системы.

СПИСОК ЛИТЕРАТУРЫ

1. Бугров Я.С. Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров, С.М. Никольский.-М.: Наука, 1980.-175 с.
2. Клетеник Д.В. Сборник задач по аналитической геометрии / Д. В. Клетеник. - М. - Наука, 1975. - 239 с.
3. Привалов И.И. Аналитическая геометрия / И. И. Привалов. - М.: Гос. изд-во физ. - мат. лит-ры, 1961. - 229 с.
4. Данко П. Е. Высшая математика в упражнениях и задачах / П. Е. Данко, А. Г. Попов. - М.: Высшая математика, 1974. - 415 с.

Дата добавления: 2015-07-25