
|
Читайте также: |
Глубина проникновения тока в материал загрузки определяется по выражению
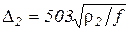 . (3.31)
. (3.31)
При расчете в «горячем режиме» значение 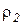 (Ом×м) соответствует значению удельного сопротивления загрузки в расплавленном состоянии.
(Ом×м) соответствует значению удельного сопротивления загрузки в расплавленном состоянии.
Глубина проникновения тока в материал индуктора определяется по выражению
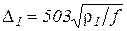 , м. (3.32)
, м. (3.32)
В (3.31) и (3.32) 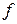 - частота источника питания, Гц.
- частота источника питания, Гц.
Активное сопротивление загрузки определяется по выражению
 , Ом. (3.33)
, Ом. (3.33)
Внутреннее реактивное сопротивление загрузки определяется по выражению
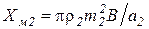 , Ом. (3.34)
, Ом. (3.34)
В формулах (3.33) и (3.34) аргумент 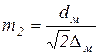 , А и В – некоторые вспомогательные коэффициенты, которые, в свою очередь, являются функциями аргумента
, А и В – некоторые вспомогательные коэффициенты, которые, в свою очередь, являются функциями аргумента  .
.
В табл. 3.1 приведены приближенные формулы для расчета коэффициентов А и В по [7].
При расчете в “горячем режиме” 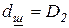 . В этом случае
. В этом случае 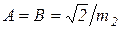 , так как
, так как  . Следовательно, активное и внутреннее реактивное сопротивления загрузки будут определяться по выражению
. Следовательно, активное и внутреннее реактивное сопротивления загрузки будут определяться по выражению
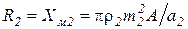 , Ом. (3.35)
, Ом. (3.35)
Таблица 3.1
Приближенные формулы для расчета
коэффициентов А и В

| А | В | Погрешность, %, не более |
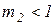
| 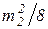
| ||

| 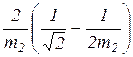
| 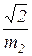
| |
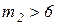
| 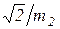
| 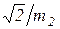
|
Активное и внутреннее реактивное сопротивления условного одновиткового индуктирующего провода определяются по выражению
 , Ом, (3.36)
, Ом, (3.36)
где 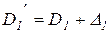 - расчетный диаметр индуктора, м;
- расчетный диаметр индуктора, м;
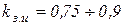 - коэффициент заполнения индуктора, равный отношению высоты индуктирующего витка без изоляции к шагу навивки. Значение
- коэффициент заполнения индуктора, равный отношению высоты индуктирующего витка без изоляции к шагу навивки. Значение 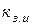 зависит от конструкции индуктора и вида изоляции.
зависит от конструкции индуктора и вида изоляции.
В формулах (3.32) и (3.36) значение удельного сопротивления меди индуктора обычно принимают  Ом×м, что соответствует температуре
Ом×м, что соответствует температуре 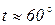 С.
С.
Реактивное сопротивление рассеяния условного одновиткового индуктора рассчитывается по выражению
 , Ом, (3.37)
, Ом, (3.37)
где 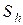 - расчетная площадь поперечного сечения воздушного зазора
- расчетная площадь поперечного сечения воздушного зазора
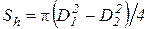 , м2. (3.38)
, м2. (3.38)
Реактивное сопротивление обратного замыкания определяется по выражению
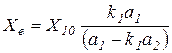 , Ом, (3.39)
, Ом, (3.39)
где 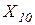 - реактивное сопротивление отрезка
- реактивное сопротивление отрезка  пустого индуктора бесконечной длины
пустого индуктора бесконечной длины
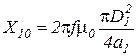 , Ом; (3.40)
, Ом; (3.40)
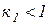 - поправочный коэффициент, учитывающий магнитное сопротивление обратного замыкания, известный как коэффициент Нагаока.
- поправочный коэффициент, учитывающий магнитное сопротивление обратного замыкания, известный как коэффициент Нагаока.
Коэффициент  можно определить как функцию отношений можно определить как функцию отношений  или или  при заданном соотношении при заданном соотношении  по графикам (см. рис 3.5) [7].
Приведенные активные и реактивные сопротивления загрузки определяются по выражениям, по графикам (см. рис 3.5) [7].
Приведенные активные и реактивные сопротивления загрузки определяются по выражениям,
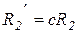 , Ом, (3.41) , Ом, (3.41)
| 
|
| Рис. 3.5. Коэффициент самоиндукции соленоида с внешним магнитопроводом |
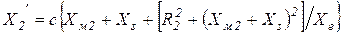 , (3.42)
, (3.42)
где 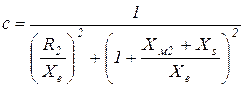 - коэффициент приведения параметров.
- коэффициент приведения параметров.
(3.43)
Эквивалентные сопротивления нагруженного индуктора определяются по выражениям
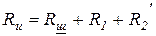 , Ом, (3.44)
, Ом, (3.44)
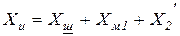 , Ом, (3.45)
, Ом, (3.45)
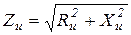 , Ом, (3.46)
, Ом, (3.46)
где 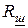 ,
, 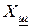 - активное и реактивное сопротивления подводящих шин.
- активное и реактивное сопротивления подводящих шин.
Коэффициент мощности индуктора определяется по выражению
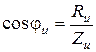 . (3.47)
. (3.47)
Дата добавления: 2015-07-25; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПРИМЕР 3 | | | ПРИМЕР 4 |